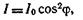Геометрическая оптика

Геометрическая оптика и фотометрия

Для сферического зеркала оптическая сила D опре­деляется формулой

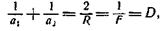
где а1 и a2 — расстояния предмета и изображения от зеркала, R — радиус кривизны зеркала и F — его фо­кусное расстояние.

Расстояния, отсчитываемые от зеркала получу, счи­таются положительными, а против луча — отрицатель­ными. Если F выражена в метрах, то D выразится в диоптриях.

При переходе луча из одной среды в другую имеет место закон преломления света

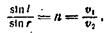
Для тонкой линзы, помещенной в однородную среду, оптическая сила D определяется формулой

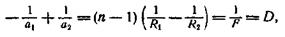
Уде at и а2 — расстояния предмета и изображения от линзы, п — относительный показатель преломления ма­териала линзы, R1, и R2—радиусы кривизны линзы. Правило знаков для линз такое же, как и для зеркал, оптическая сила двух тонких линз, сложенных вместе,

равна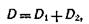

где d1 и d2 — оптические силы линз.

Поперечное увеличение в зеркалах и линзах опреде­ляется формулой

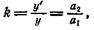
где y — высота предмета и у' — высота изображения. Увеличение, даваемое лупой,

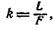
где L — расстояние наилучшего зрения и F — главное фокусное расстояние лупы.

Увеличение, даваемое микроскопом,

где L — расстояние наилучшего зрения, d — расстояние между фокусами объектива и окуляра, D4 и dz — опти­ческие силы объектива и окуляра.

Сила света I численно равна величине светового по­тока, приходящегося на единицу телесного угла:

Освещенность Е характеризуется величиной свето­вого потока, приходящегосяна единицу площади;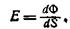

Точечный источник силой света I создает на площадке, отстоящей от него на расстоянии r, освещенность

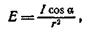
где а — угол падения лучей.

Светимость R численно равна световому потоку, ис­пускаемому единицей площади светящегося тела:

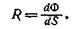
Яркостью В светящейся поверхности называется ве­личина, численно равная отношению силы света с эле­мента излучающей поверхности к площади проекции этого элемента на плоскость, перпендикулярную напра­влению наблюдения (т. е. к видимой поверхности эле­мента):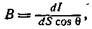

где 0 — угол между нормалью к элементу поверхности и направлением наблюдения.

Если тело излучает по закону Ламберта, т. е. если яркость не зависит от направления, то светимость R и яркость В связаны соотношением

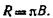
Радиусы светлых колец Ньютона (в проходящем све­те) определяются формулой

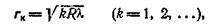
радиусы темных колец

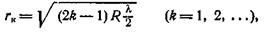
где R — радиус кривизны линзы.

В отраженном свете расположение светлых и темных колец обратно их расположению в проходящем свете.

В дифракционной решетке минимумов света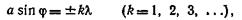

В дифракционной решетке максимумы света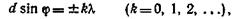

где а — ширина щели, ф — угол дифракции и k — длина волны падающего света где d — постоянная решетка

Постоянная, или период, решетки 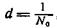, где N-число щелей решетки, приходящееся на единицу длины решетки.

Разрешающая способность дифракционной решетки определяется формулой

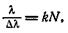
где λ — общее число щелей решетки, k — порядок спектра, λ и Δλ — длины волн двух близких спектральных линий, еще разрешаемых решеткой.

Угловой дисперсией дифракционной решетки назы­вается величина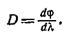

Линейной дисперсией дифракционной решетки назы­вается величина, численно равная

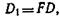
где F — фокусное расстояние линзы, проектирующей спектр на экран.

При отражении, естественного света от диэлектриче­ского зеркала имеют место формулы Френеля:

и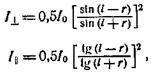

Если 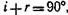то /ц=0. В этом случае угол падения i и показатель преломления п диэлектрического зеркала связаны соотношением 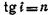(закон Брюстера).

Интенсивность света, прошедшего через поляризатор и анализатор, равна (закон Малюса)