Геометрическая оптика

Дифракция Фраунгофера от щели

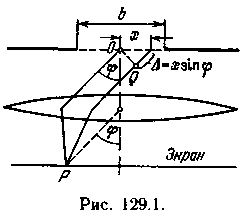Пусть на бесконечно длинную щель падает плоская световая юлна (рис. 129.1). Поместим за щелью собирающую линзу, а в фокальной плоскости линзы — экран. Волновая поверхность падаю­щей волны, плоскость щели и экран па­раллельны друг другу. Поскольку щель бесконечна, картина, наблюдаемая в любой плоскости, перпендикулярной к щели, будет одинакова. Поэтому доста­точно исследовать характер картины в одной такой плоскости, например в пло­скости рис. 129.1. Все вводимые в даль­нейшем величины, в частности угол φ, образуемый лучом с оптической осью линзы, относятся к этой плоскости.

bsinφ=±kλ (k=1,2,3..) – минимумы интенсивности.

Дифракция на дифракционной решетке Пропускающие решетки. Отражательные решетки.

Дифракционной решеткой называется совокупность большого числа одинаковых, отстоящих друг от друга на одно и то же рас­стояние щелей (рис. 130.1). Расстояние d между серединами со­седних щелей называется периодом решетки.

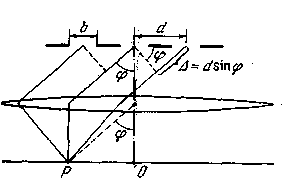Расположим параллельно решетке собирательную линзу, в фо­кальной плоскости которой поставим экран. Выясним характер ди­фракционной картины, получающейся на экране при падении на решетку плоской световой волны (для простоты будем считать, что волна падает на решетку нормально). Каждая из щелей даст на эране картину, описываемую кривой, изображенной на рис. 129.3. Картины от всех щелей придутся на одно и то же место экрана (независимо от положения щели, центральный максимум лежит против центра линзы). Если бы колебания, приходящие в точку Р от раз-. личных щелей, были некогерентными, результирующая картина от N щелей отличалась бы от картины, создаваемой одной щелью, лишь тем, что все интенсивности возросли бы в N раз. Однако коле­бания от различных щелей являются в большей или меньшей сте­пени когерентными; поэтому результирующая интенсивность будет отлична от NIФ (Iф — интенсив­ность, создаваемая одной щелью; см. (129.6)).

В дальнейшем мы будем пред­полагать, что радиус когерентно­сти падающей волны намного пре­вышает длину решетки, так что колебания от всех щелей можно считать когерентными друг относительно друга.

Таким образом мы имеем максимум дифракции ( светлые полосы ) для направлений, удовлетворяющих условию:

d · sin φ = ±m · λ (2), где m - порядок спектра, φ - угол дифракции.

Таким образом мы имеем минимум дифракции ( тёмные полосы ) для направлений, удовлетворяющих условию:

b · sin φ = ±k · λ (3), m - порядок спектра, φ - угол дифракции.

По устройству дифракционные решетки бывают про­пускающие и отражательные. Пропускающие решетки изготавливаются из стеклянных или кварцевых пластин путем нанесения алмазным резцом ряда параллельных штрихов. Промежутки между штрихами являются щеля­ми. Отражательные решетки изготавливаются нанесением алмазным резцом штрихов на поверхности металличеcкого зеркала. Лучшие решетки содержат 1200 штрихов на 1 мм решетки. Общее число штрихов у таких решеток длиной порядка 200 мм достигает 200 тысяч.