Математическое моделирование режимов работы и оптимизация параметров оптических систем СЭС
Уже при разработке первых проектов экспериментальных СЭС возникла острая необходимость в специальных методах расчета и имитационного моделирования работа оптических си тем. Специфика оптической системы СЭС проявляется в дискретности, многоэлементности и изменяющейся во времени геометрии зеркальной поверхности.
Несмотря на простоту законов, описывающих элементарное отражение пучка солнечных лучей от плоской зеркальной фацеты, дискретность системы затрудняет применение к описа нию ее работа аналитических методов, подобных методам описания работы фокусирующих систем зеркальных концентратора солнечных печей. Многоэлементность и изменение во времен геометрической формы концентрирующей системы СЭС требую1 для расчета интегрального эффекта многократного повторения однотипное вычислительных процедур, учитывающих характерно тики элементарных отраженных пучков лучей, собирающихся нг приемнике СЭС.
Эти особенности оптических систем СЭС явились предпосылками к применению машинных методов моделирования их работы и стимулировали параллельное развитие расчетных алгоритмов в различных странах [2,3,7,31,56,58,72,85,112, 145]. Для этапов становления этого направления как в CCCI так и за рубежом характерно параллельное развитие в расчет но-проектных и теоретических работ, Тесная связь между совершенствованием расчетных методов и конкретными запросаі проектной практики.
Оптическая система СЭС должна удовлетворять комплексу противоречивых технических требований и условий и представляет собой обширное поле для постановки и решения разнообразных оптимизационных задач.
Отечественная практика применения машинных методов проектирования оптических систем СЭС [2,3,7,9,31] сложилась в ходе разработок экспериментальной станции СЭС-5 и обосновывающих материалов проектирования и строительств! СТЭС промышленного уровня мощности на территории Уз. СС При работе над этими проектами были предложены методы ре шения прямых задач широкоапертурной оптики зеркальных сио тем с изменяемой геометрией. Постановка прямой задачи пре полагала непосредственный расчет оптико-энергетических характеристик заданной оптической системы, анализ характерны потерь и прослеживание динамики изменения тепловых нагруз<
на приемнике излучения. Отбор приемлемых вариантов геометрии оптической системы проводился методом проб и ошибок или прямым сравнением результатов многовариантных расчетов энергетических характеристик системы.
Этот этап позволил установить ряд априорно неочевидных свойств многоэлементных зеркальных систем и разработать систему рациональных приближений, ускоряющих процесс машинных вычислений и позволяющих моделировать все более сложные и многообразные ситуации. Это создало предпосылки для постановки обратных задач, предполагающих оперирование с целыми классами решений и предназначенных для параллельного сравнительного анализа различных глобальных геометрий оптической системы.
В настоящее время это направление развивается в плане создания программного обеспечения систем автоматического проектирования СЭС. В состав многоуровневой иерархической структуры серии машинных программ систем автоматического проектирования СЭС входят алгоритмы обработки исходной климатической информации, программы вычисления параметров обобщенных локальных характеристик затенения и блокировки зеркальных элементов, алгоритмы машинной "упаковки" зеркального поля, алгоритмы оптимального заполнения земельного участка заданным количеством зеркальных элементов и алгоритм оптимизации размеров приемника и режимных параметров теплосиловой подсистемы СЭС.
Основной проблемой разработки оптической системы СЭС является системное согласование и определение оптимального сочетания параметров зеркального поля, геометрии приемника и номинальных режимных характеристик системы преобразования энергии. Поэтому иерархия машинных алгоритмов рассчитана на параллельный анализ ряда конкурирующих оптичео - ких схем с различными типами геометрии приемника, включая варианты с несколькими приемниками, расположенными на одной башне. Целевой функцией оптимизационной задачи является среднеэксплуатационное значение полезного теплового потока, поступающего в систему преобразования энергии при заданной суммарной площади зеркальной системы.
Завершением серии программ, посвященных выбору и оптимизации оптической системы СЭС, является набор алгоритмов решения задач, предназначенный для детального анализа оптико-энергетических характеристик отобранных решений. Он основан на ранее разработанных алгоритмах прямого расчета характеристик оптической системы с заданной геометрией [ 7, 31]. Блок-схема алгоритмов представлена на рис. 8.
В имитационную модель вводятся среднестатистические климатические характеристики района расположения СЭС и географическая широта местности, nb которым во внутренни блоках модели вычисляются положения Солнца и наиболее роятный уровень прямой солнечной радиации в различное вре мя рабочего дня СЭС, в разные. сезоны года. ;
Кроме того, в модель закладываются основные геометри-j ческие характеристики оптической системы: габариты зеркал ного поля и отдельных гелиостатов, расстояния между зерка 28
лами и способ их взаиморасположения, высота башни, размеры приемника, допуск на точность ориентации гелиостатов и т. п.
Алгоритм вычисления строится в виде иерархий вложенных друг в друга, циклически повторяющихся подпрограмм. Внешние циклы организуют последовательность перебора рассматриваемой совокупности вариантов расчета и могут изменяться в зависимости от постановки задачи на данном этапе исследования.
Например, при исследовании энергетических характеристик конкретного варианта компоновки оптической системы с фиксированными геометрическими параметрами внешние циклы осуществляют перебор различных моментов рабочего дня СЭС в разные сезоны года, так что для данной оптической системы может быть прослежена динамика изменения оптических и энергетических характеристик во времени, а также могут быть рассчитаны среднегодовые значения соответствующих величин.
Другим примером может служить исследование энергетичео - ких характеристик оптической системы в зависимости от ее геометрических размеров. В этом случае внешние циклы осуществляют перебор исследуемой совокупности значений геометрических параметров систем. Таким образом могут быть определены, например, зависимости коэффициента улавливания от соотношения между размерами приемника и единичного гелиостата, зависимость самозатенения зеркальной системы от коэффициента заполнения земельного участка зеркальной поверхностью, зависимость блокировки зеркал от высоты башни и т. п. Эти зависимости могут рассматриваться для данного характерного момента времени или усредняться по дневному, месячному, сезонному или годовому периоду работы СЭС.
Внутренние циклы программы вычислений при всех указанных постановках задачи остаются, как правило, неизменными. На рис. 8 они выделены вложенными друг в друга пунктирными прямоугольниками. В качестве основной самостоятельной единицы вычислительной программы может быть принято вычисление распределения поверхностной плотности потока излучения Для фиксированной совокупности точек приемника. Эта единица вычислительной программы организуется с помсдью приведенной ниже последовательности циклов.
Внешний цикл данной подпрограммы осуществляет перебор отдельных гелиостатов зеркальной системы. Для каждого гелиостата определяются границы затененной и блокированной областей зеркальной поверхности.
Следующий по уровню вложения никл перебирает точки при-
емника. В плоскости каждого гелиостата для каждой точки приемника определяется положение и размер изображения Солнца (с учетом сшибок систем слежения).
Изображение разбивается на равновеликие по угловым размерам элементы, и самый внутренний цикл подпрограммы осуществляет перебор этих элементов. Для каждого элемента проверяется следующее:
1) расположен ли данный элемент в пределах озеркаленной области плоскости гелиостата;
2) не принадлежит ли он затененной области;
3) не принадлежит ли он блокированной области.
Отношение числа элементов изображения, принадлежащих области зеркала, свободной от затенения и блокировки, к общему числу элементов изображения, умноженное на косинус угла падения лучей от гелиостата на поверхность приемника, равно вкладу, вносимому данным гелиостатом в суммарный геометрический коэффициент концентрации излучения в данной точке приемника. При суммировании элементов изображения каждому элементу должен быть приписан вес, пропорциональной яркости данного элемента.
Суммирование элементарных вкладов отдельных гелиостатов осуществляется последними операторами цикла, перебирающего гелиостаты зеркального поля.
В процессе вычислений определяются значения ряда вспомогательных величин,^таких, как средние по полю значения фактора косинуса cos ф, фактора затенения г, фактора блокировки /3, коэффициента эффективности использования зеркальной повер> ности 7)Q, коэффициента улавливания у. значение суммарного потока Q0Tp, отраженного зеркальной системой, и суммарного потока^ Qnr, падающего на приемник.
Блочная структура программы облегчает управление процессом вычисления и допускает различные модификации, в частности вычисление распределений локальных значений факторов cosф } т, /3, TjQt не требующее обращения к блокам программы, расположенным на рис. 8. ниже горизонтальной пунктирной линии.
С помощью системы алгоритмов решения прямых задач оптики СЭС в 1978-1980 гг. были исследованы сравнительные характеристики эффективности различных структур поля гелиостатов. Предлагавшиеся на предварительной стадии обсуждения проекта СЭС-5 строго периодические прямоугольные, гексагональные и другие структуры с постоянным по всему полю коэффициентом заполнения были признаны неэффективными.
|
Ч-Н
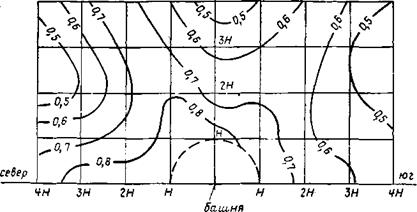
Рис. 9. Линии уровня среднегодовых локальных значений коэффициента эффективности при гексагональной структуре поля гелиостатов и Кзап = 3; Н- высота башни |
В качестве примера на рис. 9 представлено распределение эффективности использования зеркальной поверхности по площади поля гелиостатов со строго периодической гексагональной структурой. Как видно, периодическая структура имеет характерные выделенные радиальные направления с уменьшенной эффективностью использования зеркальной поверхности, обусловленной блокировкой гелиостатов.
В дальнейшем была выбрана в качестве оптимальной упоминавшаяся выше радиально-круговая шахматная структура расположения гелиостатов с переменным коэффициентом заполнения, уменьшающимся в радиальном направлении от башни к периферии зеркального поля.
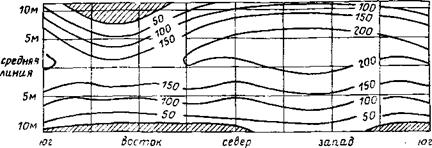
Итогом расчетов по рассматриваемой цепочке алгоритмов является распределение плотности сконцентрированного потока излучения по поверхности приемника. На рис. 10 представлено такое распределение, рассчитанное в процессе разработки обосновывающих материалов строительства четырехмодульной (каждый модуль по башенной схеме) промышленной станции СЭС - 200 в Крыму.
|
Рис. 10. Развертка боковой поверхности цилиндрического приемника модуля СЭС мощностью 50 МВт. Линии уровня (в кВт/м^) распределения плотности потока излучения для 22 сентября в 8 ч. Высота Солнца над горизонтом 0 = 20 J q = = 0,66 кВт/м^ цо условиям Крыма, Qnr= 193 МВт |