Фотоприемные устройства и ПЗС. Обнаружение слабых оптических сигналов
ЯЧЕЙКА С НАКОПЛЕНИЕМ КАК КВАЗИОПТИМАЛЬНЫЙ ФИЛЬТР
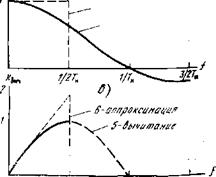
Временная форма анализа обработки сигнала и шума в ФПУ (интеграл свертки (3.140), (3.141)), сложение отдельных выборок сигнала и шума (см. § 3.6) особенно наглядно показывают, что оптимальная фильтрация не что иное, как сложение, интегрирование, накопление сигнала в течение некоторого интервала времени. Как следует из формулы для интеграла свертки (3.14), в общем случае оптимально сложение выборок с весовыми коэффициентами, соответствующими импульсной характеристике. Любой фильтр-усилитель с полосой /у можно рассматривать как устройство с эффективным временем наблюдения (накопления) 1/2 [у (см. § 3.5). Оптимальный фильтр для прямоугольного импульса длительности Тс (рис. 4.1) содержит интегратор и обеспечивает с помощью устройств сдвига и вычитания накопление в течение Тс. Выбранная в качестве ква - зиоптимального фильтра, однозвенная ^С-цепочка (рис. 4.27) также выполняет интегрирование - Схема содержит всего два элемента, и каждый осуществляет свою необходимую функцию. Емкость С — это память системы, она хранит заряд (интеграл тока сигнала). Сопротивление Я осуществляет противоположную функцию — стирает информацию через время тф^КС. В диалектическом единстве этих двух противодействующих элементов и достигается нужный эффект — накопление заряда за данное время наблюдения Хф=Т<..
Но разрядить конденсатор можно не только через сопротивление— сопротивление можно заменить ключом, периодически замыкающимся через интервалы времени Тк (рис. 4.27). При такой замене получается еще одна схема квазиоптимальной фильтрации — ячейка с емкостью и ключом. Ее простота позволяет решить одну из основных задач фотоэлектроники —■ создать многоэлементные матричные ФПУ с обработкой сигнала, близкой к оптимальной. Ведь разместить сложный фильтр с оптимальной частотной характеристикой в каждом из 103; Ю4; 105; Юв каналов, да еще на малой площади (нужны размеры фоточувствительного элемента около 100ХЮО и даже ЗОХ
|
|
|
|
|
|
|
|
|
|
|
|
|
![]()
![]()
|
№ |
![]()
|
-О |
![]() ]■ 1р)т
]■ 1р)т
О
|
|
|
|
|
|
|
|
|
|

Рис. 4.27. От оптимального фильтра к ячейке с накоплением:
А — оптимальный фильтр; б — квазиоптимальный фильтр; в — накопительная ячейка; г—функциональная схема накопительной ячейки
ХЗО мкм) было бы просто невозможно. Самой простой и универсальной схемой ячейки почти всех матричных фотоприемных устройств является ячейка с тремя обязательными элементами: фотодетектором, емкостью и ключом. Безразлично, что является накопительной емкостью — емкость ФД или ПЗС-эле - мента, что является ключом — полевой транзистор или соседний ПЗС-элемент. Безразлично, как считывается накопленный заряд— по изменению напряжения на емкости, как, например, в фотодиодных матрицах с МДП-ключом, или он передается на выход, — принцип обработки сигнала в ячейке универсален во всех одно - и двухмерных матрицах типа ПЗС, ПЗИ, пожарных цепочках, решетках и даже некоторых одноканальных ФПУ. В литературе описано применение схемы емкость —ключ для кремниевого ФД с малым темновым током [96]. В ряде приборов схема ячейки может модифицироваться. Так, в гибридных ПЗС входные устройства могут содержать дифференцирующие цепи [25, 26, 97]. В фотосопротивлении носители заряда на - калливаются непосредственно в объеме полупроводника (в валентной зоне, зоне проводимостей), а «стирание» осуществляется в результате рекомбинации. Такая ячейка эквивалентна схеме на рис. 4.27,6, причем тф=тж, где тж — время жизни. Можно использовать и другие механизмы, но всегда для оптимизации обработки необходимы накопление и стирание, что кажется само собой разумеющимся, совершенно очевидным. Но несмотря на это разрабатываются приборы и без накопительного элемента, например некоторые гибридные матрицы
[98], Конечно, здесь технически трудно осуществить накопление в ячейке из-за ограниченности емкости (см. § 1.1) > но смысл разработки такой матрицы как квазиоптимального устройства .теряется, теряется информация о сигнале, его энергия используется только в момент опроса облученной ячейки.
Из сказанного очевидно, что анализ процесса обработки. сигнала в ячейке фотодетектор-емкость-ключ — это анализ. приема сигнала практически во всех многоэлементных ФПУ с накоплением. Понятно также, что возможности такой ячейки ограничены: ее относительная частотная и импульсная характеристики заданы, так что ячейка не может настраиваться на. произвольную форму спектра сигнала. Понятна и очередная наша задача — определить потери в отношении сигнал-шум такой ячейки по сравнению с оптимальным фильтром.
Ячейка емкость-ключ как оптимальный фильтр. Найдем заряд Q, который накапливается на емкости С (рис. 4.27, в). Периодически с периодом Тп ключ замыкается и заряд на емкости стирается, так что период Гн и будет интервалом накоп - ■ ления. Сброшенный с емкости заряд передается на выход, где и регистрируется. При таком методе опроса выборки (моменты опроса) совпадают с моментами стирания, период между (выборками Гв совпадает с интервалами накопления 7V-
Г
Q - I(t)dt, ' (4.231)
О,
;где I (t) —реализация тока ФП.
Перепишем эту формулу в виде
Оо
Q= [ H(t)I(t)dt, (4.2S2)
—ОО ‘
Где
//(/) = 1 при О<t<Tn ^
H(t)= 0 при t<i0, (4.233)
Из этого представления сразу же становится очевидным, что импульсная характеристика ячейки емкость-ключ является единичной прямоугольной функцией длительности Тв. Отсюда согласно § 3.6 следует, что ячейка является оптимальным фильтром при трех условиях: форма входного сигнала является тоже прямоугольной; моменты опроса (выборки) совпадают с началом (и концом) входного импульса, при этом время^ накопления равно длительности импульса Та~Тс; шум белый.
С подобной прямоугольной импульсной характеристикой несколько раз встречались в § 3.5, 4.1, 4.3, где она относилась к
Преобразователям ток — напряжение, поэтому ее размерность Ом/с. Наша ячейка с накоплением является преобразователем ток—заряд, и размерность ее коэффициента передачи К0[с], поэтому импульсная характеристика оказалась безразмерной; [размерность Н]= [размерность /С]/с=с/с= [безразмерная величина].
С расчета отношения сигнал-шум для такого классического случая начинали анализ (см. § 3.3, (3.57)). Эту же формулу можно получить, непосредственно рассматривая заряды, накапливаемые на емкости. Флуктуация темнового (а при наличии фона —и фонового) тока h{t) приведет и к флуктуации зарядов Qi, Q2,. .., накапливаемых в разных кадрах, т. е. на последовательности временных интервалов 0 ... Гн; Гн...
... 27V, ...; (п—1)Тн...пТн■ Средние значения по этим кадрам для заряда и числа электронов равны
Q0=70r„; iV„=70r,,/?. (4.234)
Поскольку флуктуации подчиняются статистике Пуассона, то аналогично (4.141)
AAV — Nq. AQo2 = <72Д Лг02 = q2N о = gQ0 — qi о Т н. (4.235)
При наличии оптического сигнала Ес возникает дополнительно сигнальный фототок SEca, подзаряжающий емкость на величину сигнального заряда (рис. 4.28, а, б):
Qc~SEcATc. (4.236)
Отношение этого сигнального зарада к. шумовому при условии Ти = Т0
А'аш=Qc/УЁЩ= SEtbT'/Vqitfc=
<J>nl = J/2?VS, (4.237)
Совпадает с классическим выражением (3.57), т. е. при трех сформулированных условиях накопление на интервале Тс является оптимальной обработкой сигнала.
Рассмотрим теперь потери накопительной ячейки в отношении сигнал-шум по сравнению с оптимальным фильтром, когда эти условия нарушаются.
Влияние формы оптического сигнала. Накопленный заряд определяется площадью под кривой сигнального фототока
|
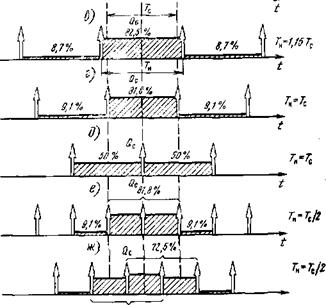
З) 72,5% Рис. 4.28. Накапливаемые заряды зависят от взаимного расположения сигнала и выборок: а, в — формы входных оптических сигналов; б, г — з — положения моментов опроса |
Между интервалами накопления. Для колоколообразного сигнала при оптимальном расположении выборок (рис. 4.28, в, г) получим
|
|
■^аТ'с[27-с + я 51п^ 2 т-")^ ТхчС2Гс;
<2с=8ЕсАГс, Т„ > 2ТС. (4.238)
|
ЗЕСА^1 с/У н> Тн ^ 2Гс* |
![]()
|
(4.239) |
![]() Как следует из (4.238) и (4.239), при малом времени Т с ростом
Как следует из (4.238) и (4.239), при малом времени Т с ростом
Тн отношение сигнал-шум возрастает: а при
Большом оно начинает падать: Агс;ш^ 1/1/Г^н» так как при
|
(4.240) (4.241) |
![]() 7’н^:2Т’с сигнал накапливается полностью и при дальнейшем росте Тн накапливается уже только один шум. Максимум отношения *ГС! Ш достигается при некотором оптимальном времени Тво^. Полагая производную от (4.239) равной нулю, на
7’н^:2Т’с сигнал накапливается полностью и при дальнейшем росте Тн накапливается уже только один шум. Максимум отношения *ГС! Ш достигается при некотором оптимальном времени Тво^. Полагая производную от (4.239) равной нулю, на
Ор<= 1,149 Тс,
А'с/ш (Гн ОР0 = 1,167 ЯсА УТ1/ФЛ.
Из § 4.1 известно, что кривые настройки (зависимости отношения Лгс/Ш от ПОЛОСЫ (следовательно, и ОТ Времени Гн) пологие, .поэтому нет необходимости строго соблюдать соотношение (4.240). На практике удобно, как и при прямоугольном сигнале, выбрать время накопления равным просто эффективной длительности сигнала. Дополнительные потери в отношении Л/с/;ш составляют всего около 1% (рис. 4.28, д):
|
(4.242) |
![]() ТН = ТС, ДГс/ш^1Л56Яс/Гс/Фп1.
ТН = ТС, ДГс/ш^1Л56Яс/Гс/Фп1.
Как видно из рис. 4.28, в—д, при колоколообразном сигнале удается накопить только 82% от всего заряда сигнала (при прямоугольном сигнале заряд накапливается полностью, рис. 4.28,6). Но ведь и при оптимальной фильтрации для колоколообразного сигнала отношение ЛГС/Ш падает на 13,5% (по сравнению со случаем обнаружения прямоугольного импульса, табл. 3.2). Так что потери накопителя по сравнению с оптимальным фильтром при приеме колоколообразного сигнала составляют всего 5%, даже меньше, чем для однозвенного ква - зиоптимального ЯС-фильтра (4.62), (4.68).
Влияние асинхронности опросов и моментов прихода сигнала. Интервал накопления и период выборок. До сих пор рассматривали случай, когда опросы (выборки) были строго синхронизированы с заданным положением сигнала на оси времени и расположены наилучшим образом, т. е. в одном из кадров накапливался максимальный заряд (рис. 4.28, а—д)> Однако на практике в подавляющем большинстве оптико-электронных систем момент прихода сигнала неизвестен, так что взаимное расположение сигнала и опросов случайно. На рис. 4.28, е показан наихудший из возможных случаев, когда пришедший сигнал делится пополам между двумя соседними
кадрами. В этом случае накопитель уже достаточно заметно проигрывает оптимальному фильтру — на 50% при прямоугольном сигнале и на 42% при колоколообразном:
ЛГс;ш=0,5 5ЯсаГс/У^Тс=0,707Еса 1/Гс/Ф„,. (4.243)
Так приходится расплачиваться за то, что в ячейку ввели нестационарный элемент (ключ), параметр которого — сопротивление меняется во времени. Схема стала параметрической, и ей можно приписать фазочастотную характеристику, зависящую от времени — момента включения ключа. Когда эта частотная характеристика ячейки не сфазирована со спектром сигнала, получаем проигрыш в отношении Лтс/Ш. Оптимальный же фильтр (рис, 4,27, а, (4.1)) стационарен. Заложенная в нем память (линия задержки) позволяет всегда на выходе получать амплитудное значение сигнала иса через некоторое, строго определенное время после любого момента прихода сигнала. Это и обеспечивает инвариантность параметра Мс/Ш относительно любого момента прихода сигнала (0.
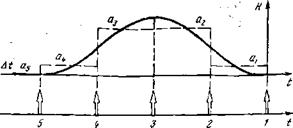
Рассмотрены предельные случаи наилучшего (рис. 4.28, а—д) и наихудшего (рис. 4.28, е) расположения выборок. Рассмотрим теперь промежуточную ситуацию (рис. 4.29). Выборку совместим с нулевым моментом времени (рис. 4.29, а). Интервал интегрирования указан на рис. 4.29, б, где прямоугольная функция Н{ДО—импульсная характеристика накопителя при ^о^О. Перемещая сигнал по оси времени, легко найти накапливаемый заряд при любом произвольном положении сигнала (рис. 4.29, в—ж). Этот заряд равен площади перекрытия сигнала с прямоугольной импульсной характеристикой Н{Ы). Ясно, что при прямоугольной форме сигнала заряд <2С оказывается линейной функцией Времени Д/=^0—^пер> ГЛе ^пер— момент прихода сигнала (положение фронта). Ну конечно же, и рис. 4.29, и методика расчета выходного сигнала ячейки — накопленного на ней заряда С? с(Д£) нам хорошо знакомы! Ведь точно также рассчитывалась форма сигнала на выходе оптимального фильтра (рис. .3.20): сигнал в любой текущий момент тоже равен интегралу входного тока за предшествующий интервал Т
1 н>
Отмеченная аналогия весьма важна, она помогает сделать последний шаг в формальном преобразовании эквивалентной схемы ячейки — заменить емкость и переключатель двумя функциональными блоками (рис. 4.27, в, г). Первый блок — это стационарный (непараметрический) накопитель с временем Тн, полностью аналогичный указанной схеме на рис. 4.1 —фильтру, оптимальному для прямоугольного сигнала. На выходе его возникает непрерывный сигнал фс(Д0* Второй функциональный блок, выполняющий мультиплексирование (коммутацию) с периодом 7,в=7,ш берет выборки этого сигнала <2с(А0- Так
Рис. 4.29. К расчету сигнала (заряда) фс на выходе накопителя в зависимости от текущего времени
Получили функциональную схему* которую и должно иметь многоэлементное ФПУ и с которой начиналась книга (см. § 1.1, рис. 1.1, а). Эта схема на рис. 4.27, г справедлива для любой формы входного сигнала. По описанной методике можно рассчитать сигнал <2с(Л0 при колокообразном входном импульсе (рис. 4,29,3, где /пер определяется по уровню 0,5 фронта) .
Полученная функциональная схема ячейки позволяет конкретизировать причину наших неприятностей. Собственно интегратор практически идеален; было показано, что при прямоугольном сигнале он вообще не дает потерь, а при колоколообразном уступает оптимальному фильтру всего на 5%>
Неприясности связаны с коммутацией. В одноканальном ФПУ коммутатор не требуется, можно непрерывно наблюдать за выходным сигналом, и поэтому всегда зарегистрируем максимум сигнала. В многоэлементном ФПУ вынуждены брать дискретные выборки с выхода каждого канала. Конечно, период выборок должен быть достаточно мал, чтобы «не прозевать» максимум выходного сигнала. В традиционном ФПУ с усилителем в каждом канале и последующим коммутатором постоянная накопления Тя (по сути, это эффективная постоянная времени усилителя ta) не связана с периодом выборок коммутатора. Естественно, в таких устройствах время Тв также ограничено и тоже могут возникнуть потери из-за асинхронности опроса, но все-таки можно обеспечить ТВ<^.ТЛ и сделать эти потери малыми. Недостаток ячейки с накоплением как раз и заключается в том> что у нее очень большой период выборок ГВ=ГН, сопоставимый с постоянной времени изменения выходного сигнала Тс. Выборки могут «проскочить» максимум Qc{&t), что и приводит к потерям вплоть до 42... 50% в регистрируемом сигнальном заряде (рис. 4.28, е).
Итак, из-за того, что выборки редкие и не сфазированы с сигналом, отношение Nc/m может меняться в достаточно широких пределах 0,5 ... 1 (при прямоугольном импульсе) и 0,58 .. Л (при колоколообразном). Эти значения Nc/m были получены при оптимизировании времени накопления Гн при благоприятной ситуации — расположение выборок симметрично относительно максимума (центра) сигнала, поэтому в один из кадров (выборки 2...1) попадал наибольший заряд (рис. 4.30, а, б). Теперь проделаем операцию оптимизации времени Тн для наихудшего случая: зафиксируем одну из выборок (выборку /) в максимуме (центре) сигнала (рис. 4.30, в). В этом случае в каждый из соседних кадров (2—1, /—0) может попасть не более половины сигнального заряда. Из рис. 4.30, в особенно наглядно видно, что для прямоугольного импульса период накопления ТН=Тс завышен. Лишь одну половину этого периода накапливается сигнал, а другую — только шум. Ясно, что для прямоугольного импульса надо выбрать Tn—Tcj2. Тогда сигнал сохранится прежним: Qc —0,5SЈ, cA7’c> зато шум уменьшится в раз:
|
(4.244) |
![]() Ncm^Qjџ?/0Гс/2 = =£са VTt (S/VWа = Јca VTj0„v
Ncm^Qjџ?/0Гс/2 = =£са VTt (S/VWа = Јca VTj0„v
|
|
|
А * И орт/ I с 11иАи птираю 1п ирп гОЛ ОКОЛООбраЗНОМ Импульсе. При превышении этого времени шум растет быстрее сигнала. Один раз это уже было доказано для наилучшего по- |
|
Точнее — время |
Рис. 4.30. Оптимизация времени накопления при неблагоприятном расположении выборок
Ложения выборок (рис. 4.28, г). В теперешнем случае сигнал (кадр 1, рис. 4.30, г) делится просто пополам: <3С=
= (0,818 8ЕсАТс) /2, и получаем
Л'с, ш=<3</|/1Щ= 0,409 5£,сАГс/'К?/о7'с/2=
= 0,818 ЕсАуТс/Фп1. (4.245)'
При таком уменьшении времени накопления отношение Л'с/ш вообще перестает зависеть от временного положения выборки при прямоугольном импульсе и весьма слабо зависит при колоколообразном (рис. 4.30, г, д):
Л'с„„ = <Зс/1/ЩГ = (0,409 ... 0ЛЩ/У ч1„Тс/2 =
= (0,818 ... 0,95) ЯсА у'7/Ф„,. (4.246>
Хотя теперь и не достигли максимального значения (4.237), (4.242), но и не опустились до минимума (4.243). При любом положении выборки получаем некоторое среднее значение сигнала и его отношения к шуму (4.245), (4.246). Хорошо - это или плохо? Как видно из § 3.1, ошибки обнаружения отнюдь не линейно связаны с отношением Ыс/шу падение Л'с/ш приводит к резкому увеличению ошибки. Поэтому важно не' допускать снижения Л^с/Ш. Этого можно достичь, вдвое умеяь^ шив накопление — выбрав Та=Тс/2.
И все же остается еще ВОЗМОЖНОСТЬ улучшения отношения #с/ш примерно на 30... 40% (СР - (4.244), (4.245) с (4.237), (4.242)). Чтобы использовать этот запас, надо «развязать» времена Гв и Т’н. А сейчас по порядку изложения надо рассмотреть отступление от последнего, третьего условия — условия белого шума.
Избыточный шум типа 1// [102]. Реально отклонение от белого характера шума может возникнуть из-за избыточного шума типа 1//. В качестве примера матрицы с таким шумом назовем гибридный ИК ПЗС, где избыточный шум «любит» появляться как в фотосопротивлении (в PbS-OP или КРТ-ФД, особенно при смещении), так и во входном устройстве ПЗС (особенно при заметном входном токе) [99—101].
Попытаемся найти флуктуацию заряда при наличии избыточного шума. Будем рассматривать накопитель как обычный линейный преобразователь, на вход которого подается ток—. при расчете избыточных шумов задается спектр избыточного входного тока (2.134) — (2.138):
2ql ofн/ f. (4.247)
На выходе регистрируется заряд, для расчета которого надо знать коэффициент передачи преобразователя ток — заряд — частотную характеристику накопителя. Поскольку импульсная характеристика накопителя известна — она прямоугольная: (4.233), то ее спектр
Хинт (f)=smnfTHfnf=Kok (/);
Ко = Тк, k{f)=smnfTJnfTH (4.248)
И будет искомой частотной характеристикой накопителя (см.
§ 2.1, а также табл. 4.1). Из табл. 4.1 следует, что эффективная полоса накопителя как для сигнала, так и для белого шума равна 1/27н. Введя формулы (4.247), (4.248) сможем найти и флуктуацию заряда при избыточном шуме
00
Ъ
Со
=2 ■? Л (sin nfTjnfTtf df If. (4.249)
О
В окрестности нулевой частоты, где относительная частотная характеристика накопителя £(/) = 1, (4.249) упрощается:
А этот интеграл при /->0 расходится.
U 0
*1з-за того, что преобразователь-накопитель пропускает все Низкие частоты, на которых мощность избыточного шума тео-
Ретически бесконечна, дисперсия заряда получается бесконеч. н°й. Значит ли это, что при избыточном шуме накопитель принципиально непригоден для обнаружения слабых сигналов?
Простое однокадровое накопление действительно непригодно. Но если добавить межкадровую обработку, например вычесть заряды двух соседних кадров С}1 и <32, то снимем отмеченную неприятность — дисперсия шума уже не будет бесконечной:
|
|
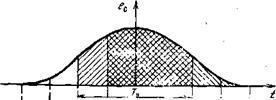
Действительно, низкочастотная флуктуация — это медленная флуктуация. Поэтому ток I{t) очень медленно меняется в течение кадра Тп и накопленные в соседних кадрах заряды Qt и Q2 почти равны, т. е. очень мала их разность — шум после операции вычитания (рис. 4.31). Преобразуем (4.250):
Н
|
(4.251) |
![]() Dt.
Dt.
О
В (4.251) переставлен порядок линейных преобразований: сначала находим приращение тока Д/(?) через время Гн, а затем
|
^-аппроксимация 3- интегратор |
|
1/2тл г/гг— тъ *киг d) |
|
*—/ |
|
І ї й кайр I }-ц кадр |
|
Т* |
|
|||
|
|||
 |
|||
|
|||
|
|||
|
|
||
|
|||
Интегрируем это приращение. Рисунок 4.31 наглядно иллюстрирует возможность такой перестановки. Таким образом, над входным током теперь производится два линейных преобразования: операция задержки на время Тн и вычитания, а потом уже известная операция интегрирования полученной разности (приращения А/(0). Поэтому в формулу для расчета шума (4.249) надо ввести еще один множитель — частотную характеристику вычитателя. А эту характеристику найти очень просто. При гармоническом входном сигнале /Bx = /fisin2jift на выходе вычитателя со сдвигом Гн получаем
/вых(0 =IBx{t)—hx{t—TK) —Is sin 2nft—
—Is sin 2nf{t~TR) = 2sin nfTJs sin 2л/(f— Tn/2). (4.252)
Дополнительный линейный множитель и есть амплитудно - частотная характеристика (АЧХ) операции вычитания
KBti4 = 2smnfTH. (4.253)
Интерпретация этой характеристики также проста. Постоянная составляющая и низкочастотные гармоники, период которых 1 if очень велик по сравнению с интервалом Гн, при вычитании, естественно, исключаются: К выч О*
Напротив, при
Сдвиге на половину периода гармоники складываются — отсюда множитель «2».
Введем полученный множитель К выч в выражение для шума заряда (4.249):
Оо ‘ 1 . - ,
ДЙ = 5 К1ь„к1„7ч/ =
О
І
СО
|
(4.254) |
![]() = ^[2sanfT,,si^ffT^ 2qhf-j-df.
= ^[2sanfT,,si^ffT^ 2qhf-j-df.
0 s
|
(4.255) |
![]() Выражение (4.254) можно представить в виде Щ = (2?/„7-н) (/BrH) Jn = (2?/07’я) (fHT„) 2,77. где
Выражение (4.254) можно представить в виде Щ = (2?/„7-н) (/BrH) Jn = (2?/07’я) (fHT„) 2,77. где
Со сс
Jn=с *l, d{=5 (2 щ f=
О 0 '
= 4 In 2 = 2,77.
Частотная характеристика накопителя с вычитанием кадров приведена на рис. 4.32, а, а на рис. 4.32,б, в приведены раздельно ее сомножители — частотные характеристика интегратора и вычитателя соответственно. Как всегда, простые аплрок-
Я21
Симации помогут пояснить физику и качественно оценить численное значение интеграла (4.256). Аппроксимация дЛя частотной характеристики интегратора £инт(!) стандартна—, считаем Авнт = const в эффективной полосе 1/2Гн (кривая 4). В вычитателе основное — это завал на низких частотах. При f</TH получаем
Квыч = 2sin nfTa&2nfTx. (4-257)
Проще всего для Квыч([) использовать эту линейную аппроксимацию (кривая 6), и тогда общая характеристика примет вид
1/2Гн; /(=*иит/е»,,«2я/Гв. (4.258)
Каждая из операций формирует необходимый спад: вычитание — спад на низкой частоте (чтобы не пропускать избыточный шум), а интегрирование — на высокой (соответствующей полосе сигнала 1/2Тс), Оценка интеграла избыточного шума (4.255) при такой аппроксимации
1 /2 Г„
Jn= 5 (2л/т^Ц-
1/2Ги
Достаточно близка к его точному численному значению (4.256).
Так обстоит дело с шумом. А как ведет себя при вычитании сигнал? Он может несколько уменьшиться, поскольку сигнальный заряд накапливается и в первом (фсО, и во втором (фсз) кадрах. Самый большой сигнал <3С1 накапливается, когда выборки расположены оптимально (рис. 4,28, д). В этом случае
Д(?с = С2с,—С? с2 = 0,82<2с—0,091<?с = 0(725£са7,с. (4.259)
В другом предельном случае, при самом «плохом» расположении опросов относительно сигнала (рис. 4.28, е), когда основной заряд (первого кадра) мал, во втором кадре, к счастью, сигнальный заряд не накапливается, так что вычитание не приводит к дальнейшему снижению сигнала:
Лфс = <3с1—Фс2=0,5С,)с—0‘(2с = 0,55£са7с.
Найдя сигнал и шум, можно, наконец, найти и их отноше-
Ние:
Хс/ш — AQc/^AQo2 =
= (0,5 ... 0,72) SEcllTc/V 2qhTc%77f„Tt = =0,3 ... 0,43£сД/Ф„, YJU.
Сравним (4.260) ^с формулой для оптимального фильтра (3.80). Потери ячейки оказываются относительно малыми и могут составлять около 26% (в худшем случае из-за асинхрон - ности опроса они возрастают до 49%). Именно вычитание помогло завершить формирование частотной характеристики ячейки, приблизив ее к оптимальной (ср. кривые и 2 на рис. 4.32). Оптимальная характеристика / рассчитана по (3.46), (2.14) и
Такое хорошее совпадение частотных характеристик /, 2 не удивительно: в § 3.5 отмечалось, что оптимальный фильтр осуществляет вычитание. Аппроксимация импульсной характеристики оптимального фильтра на рис. 3.9 позволяет рассматривать его алгоритм обработки сигнала тоже как вычитание кадров, но не двух, а трех — из заряда основного кадра 1 вычитается по половине зарядов двух соседних с ним кадров 2, 3. Поэтому изложенную методику расчета отношения Мс/Ц1 можно применять и для приближенной оценки этого отношения в оптимальном фильтре.
Суперпозиция кадров. Недостатки однокадрового накопления: строгая заданность импульсной и соответственно частотной характеристик, а также заданность периода выборок, который нельзя сделать короче интервала накопления. Это, как было показано, может приводить к заметным потерям, а при избыточном шуме однокадровая обработка вообще становится невозможной, и переходим к простейшему методу межкадровой обработки: из накопленного заряда <^1 вычитаем заряд предыдущего подкадра <32- Но ведь в принципе можно осуществить линейную суперпозицию п подкадров с произвольными коэффициентами а*:
П
Подбирая нужным образом коэффициенты а{, получаем ступенчатую аппроксимацию для любой требуемой импульсной характеристики, и чем больше число подкадров п, тем точнее аппроксимация (рис. 4.33). Однако использование метода суперпозиции кадров при большом числе п проблематично и связано с принципиальными аппаратурными трудностями:
Примерно в п раз уменьшается заряд каждого подкадра, так что вклад последующих шумов переноса заряда и выходных устройств возрастает;
Примерно в п раз становится выше частота опроса, она может стать выше технических возможностей матрицы, могут возникнуть дополнительные искажения сигнала;
Требуется в п раз большая внешняя память, усложняется алгоритм и увеличивается число операций обработки сигналов во внешних устройствах.
|
|
|
, Рис. 4.33. При суперпозиции большого числа кадров Импульсная характеристика приближается к оптимальной |
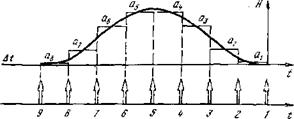
И опять на помощь приходят квазиоптимальные методы. Они значительно проще оптимальных, а потери в отношении Л'с/Ш могут быть весьма малыми. Простейший квазиоптималь - ный метод: разбить кадр ТИ = ТС на п равных подкадров Т/ = = Тн/п и последовательно складывать заряды всех этих подкадров, Сначала сложить выборки 5, 4, 3, 2( затем 4, 3, 2, 1 и так далее, как это изображено на рис. 4.34. Что изменилось? Эф-
|
|
1- А (I________________________
В 7 в 5 4 7 1
Рис. 4.34. Квазиоптимальный метод суперпозиции кадров повышает частоту опроса, не снижая эффективного времени накопления
Фективное время накопления сохранилось — оно такое же, как и при однокадровом накоплении. Зато в п раз увеличилась’ско - рость опроса коммутатора, ТВ^ТЯ'. Так удалось развязать интервал накопления и период выборок, уменьшить время гв. Ведь большое Гв и было основной причиной потери сигнала, функциональная схема на рис. 4.27, г теперь совершенно не отличается от схемы традиционного ФПУ. В ФПУ тоже приходится вводить коммутатор. Время выборки в ФПУ, а теперь и в матрице с нашей ячейкой не зависит от эффективной полосы усилителя (накопительной ячейки). Потери в сигнале из-за коммутатора становятся в матрице с накоплением такими же, как в традиционном ФПУ с усилителями.
Методика расчета величины сигнала от периода выборок Тв = Тя1п была получена ранее (рис. 4.29). Приведенная на рис. 4.29 зависимость заряда на выходе интегратора (?С(Д^) позволяет, полагая найти сигнал 0С(ТВ) =<3с{Тс/п), а
Затем и его отношение к шуму (рис. 4.35,а). Уже трех—пяти подкадров (трех—пяти выборок в течение эффективной длительности сигнала Тс) бывает практически достаточно, чтобы не пропустить максимум сигнала.
Описанный метод упрощает алгоритм обработки, но все же требует хранения сигналов всех п подкадров во внешней памяти. Функцию запоминания зарядов предыдущих подкадров можно возложить и
,09
С/и
На саму накопитель - й^.отн. ед. ную ячейку. При опросе просто-напросто надо «сливать» и считывать только /мо часть от накопленного в ней заряда, тогда сохранившаяся (1—к)-я
Часть будет нести информацию о предыдущих кадрах. Для этого организуется вторая
Рнс. 4.35. Зависимость отношения сигнал-шум при Двух квазиоптимальных методах суперпозиции кадров (заряд отнесен к полному заряду сигнала 5ЕС,ТС; форма входного импульса — коснн'с-квадратная; п =
-7УГВ):
£ — сложение п подкадров пби ■=> ; б — метод неполного слива заряда
приемная емкость — сток Сст и второй переключатель Кг. связывающий основную накопительную емкость с емкостью стока (рис. 4.36, а) ч Теперь при замыкании ключа К2 с накопительной емкости Сп на емкость стока Сст стекает следующая часть от накопленного заряда (Зн:
Qcт~'' СстФн/ (Сст4"Сн) к — ССт/(ССу~-Сп). (4.262)
Затем ключом Кл заряд (2СТ, как и в обычной ячейке, полностью передается на выход, где и регистрируется. Ключи могут представлять собой МДП-транзисторы либо ПЗС-затворы Между ПЗС-ЯЧеЙКаМИ — НакОПИТеЛЬНОЙ Сн И СТОКОВОЙ Сст - Импульсная характеристика ячейки приведена на рис. 4.36,6. Если бы заряд стирался полностью, то она была бы обычным прямоугольником длительностью Тв (заштрихованная область). Однако при неполном стирании на накопительной емкости сохранился заряд и от предыдущего кадра — но лишь его (1—&)-я часть, поскольку к-я часть была слита в момент опроса 1 = (рис. 4.36,6). Поэтому второй интервал накопле-
НИЯ — 2Та..'Тв отображается также прямоугольником, Но
Уменьшенным — это отражает коэффициент (1—&). После накопления на третьем интервале —ЗГВ. . _ —2Тъ успело уже произойти два опроса, так что амплитуда прямоугольника равна (1— &)2 и т. Д. Поэтому для любого интервала Д* = £опр—где /опр — момент опроса, і — момент прихода сигнала, имеем
Н (ДО =* (1 — А)^-1) ---- ехр [(я — 1) 1п (1 — А)] =
|
(4.263) (4.264) |
![]() =ехр [ — 0г — 1) Гв/тэ]; т„ = Гв/[— 1п (1-й)].
=ехр [ — 0г — 1) Гв/тэ]; т„ = Гв/[— 1п (1-й)].
Выражение (4.264) определяет эквивалентную постоянную времени разрядки накопительной емкости. Когда коэффициент деления мал, это выражение принимает совсем простой вид:
|
|
|
(■4.265) |
|
(4.266) |
![]() При частом сливе заряда мелкими порциями (6<С1, Тв^тэ) импульсная характеристика накопителя становится экспоненциальной, как у обычной ^С-цепочки. Физика этого чрезвычайно проста. Разрядка емкости через сопротивление ^ за малый промежуток времени (И пропорциональна полному заряда на этой емкости:
При частом сливе заряда мелкими порциями (6<С1, Тв^тэ) импульсная характеристика накопителя становится экспоненциальной, как у обычной ^С-цепочки. Физика этого чрезвычайно проста. Разрядка емкости через сопротивление ^ за малый промежуток времени (И пропорциональна полному заряда на этой емкости:
6<2 = Иы! к = О. ЬЦСК = С?6//тэ.
|
(4.267) |
![]() Точно так же разряжается и накопительная емкость за малый период б^даГв^Тэ, ведь из (4.262) следует
Точно так же разряжается и накопительная емкость за малый период б^даГв^Тэ, ведь из (4.262) следует
6Q = Qcт = kQн = QнTвf(T]i|k).
Сравнивая (4.266) и (4.267), опять приходим к тому же значению (4.265) эквивалентной постоянной времени разрядки накопительной емкости тэ = Тъ/к.
Поскольку импульсная характеристика Я(Д^) найдена, то методика расчета сигнала и шума не требует дополнительного комментария. Из рис. 4.36, б, в видно, что от накопленного в каждом п-подкадре заряда <3СП к моменту опроса /Опр = 0 на емкости Сн сохранится его ((1—&)п-1)-я часть. Сигнальный заряд (Зс(^опр) находится суперпозицией заштрихованных на рис. 4.36,6 элементарных площадей с весом Н(Д£) = (1—й)71"1. Накапливаемые в каждом подкадре темновые_ (и фоновые) заряды одинаковы: (2й=10Тв. Их дисперсии Д<2т2==^т7,в склады
ваются с весом Я2(Д0 = (1—Л)Я{П'"1)» поэтому для шума имеем выражение
00
Т=2 Ч1„тл-(-к)ц=
При подсчете суммы учтено, что ее члены представляют собой геометрическую прогрессию со знаменателем (1—к) .
По описанной методике был проведен расчет сигнала и шума при колоколообразной форме входного сигнала. Зависимость отношений А^/щ построена на рис. 4.35,6. Параметром здесь является ЧИСЛО П—Тс/Тъ, уже известное по первому методу сложения подкадров. Но теперь появилась еше одна степень свободы, еще один параметр — коэффициент деления к. При малых значениях ^ ячейка идентична однозвенному ^С-фильтру. При таком фильтре отношение сигнал-шум достигает своего максимума, когда эффективная постоянная фильтра тэ равна (почти равна) длительности сигнала Гс (см. § 4.1). Это условие обеспечивается (4.265), если коэффициент деления к выбрать обратно пропорциональным числу выборок п:
К^1!п^Тв/Тс-, тэ=Тв/к = Тв1(Тв/Тс) = Тс. (4.269)
Рисунок 4.36, б полностью подтверждает сказанное: предельное для данного метода отношение Агс/ш даже при асинхронном опросе такое же, как и у однозвенного #С-фильтра. Причем оно достигается уже при 3 ... 5 выборках за время Тс. Столько же выборок (подкадров) оказывалось достаточным и в методе сложения кадров. Вертикальными отрезками на рис. 4.36,6 обозначен диапазон изменения отношения Лгс/ш при выборе других значений к. Поскольку при малых числах п= 1, 2, 3 еще проявляется ступенчатая форма импульсной характеристики, то, строго говоря, принятые значения к—/п могут быть неоптимальными. Поэтому выбирались и такие значения к, когда отношение Л^с/ш становилось максимальным либо при наихудшем расположении выборки либо при ее наилучшем расположении (см. точки на рис. 4.35, в, обозначенные соответственно крестом либо кружком). Вариации коэффициента ^ приводят к достаточно малым — около 1 ... 15% — вариациям отношения Лс/ш и то только при п = 1, 2, что в общем-то неудивительно. Еще раз подтвердили ВЫВОД о некритичности Мс/ш к точности настройки системы.
Таким образом, предложенный метод неполного слива позволяет примерно в 1,5 раза увеличить отношение Лтс/Ш по сравнению с простым однокадровым накоплением (сравните точки п= 1 и п = 5 на рис. 4.36,6 при неблагоприятном положении выборок). Выигрыш почти такой же, как и в методе сложения кадров. Какой же из них выгоднее? Ответ зависит от системы: если усложнение матрицы нецелесообразно, то следует использовать метод сложения кадров, а если нецелесообразно усложнять внешнюю обработку, то надо применять метод неполного слива.
И еще одно преимущество рассмотренных методов — увеличение частоты опроса по сравнению с простым накоплением примерно в 3...5 раз, а это важно для систем, где существенна точность определения координаты источника излучения.
Накопление постоянной составляющей. В традиционном ФПУ разделительный конденсатор не пропускает постоянную составляющую тока ФП на выход усилителя. В накопителе равным образом накапливаются носители заряда, генерированные как сигналом, так тепловым и фоновым излучениями. При большой величине постоянного тока /0 это приводит к двум неприятностям.
Первая — пороговые сигнальные заряды приходится выделять из смеси с очень большим постоянным зарядом Со. Отношение постоянной составляющей к шуму
СыУ =<2о//?0^ = УТ5о/7 = УЖ (4.270)
Пропорционально корню из числа накопленных электронов (см, § 4.3, (4.154)). Для типовой удельной емкости (3... 5).
• 10-8 Ф/см площадки Л3 = 30X30 мкм2 = 9*10-6 см2, Д£/ = 5 В имеем следующие численные значения:
|
Сн= (3... 5). 10~8-9- 10-е= (2,7 ... 4,5) • 10"13 Ф |
(4.271) |
|
<2о = СнД £/= (2,7 . . . 4,5) • 10-13; 5= |
|
|
(1,35 .,. 2,25) • 10~12 Кл, |
(4.272) |
|
No = Qo/q= (1,35 ... 2,25) • 10~12/1,6-Ю"19^ 107; |
|
|
Т^ЛГо-ЗООО. |
(4.273) |
|
Получили правило трех тысяч: при заполнении |
Типовой емкости накопителя отношения постоянной составляющей к шуму и сам шум (число шумовых электронов) весьма велики, по порядку величины равны 300 0.
Вторая неприятность — ограничение времени накопления. Если напряжение на накопительной емкости Сн может изменяться в пределах |ДС/|, то при токе /о максимально допустимое время накопления равно
Гнтах = с„|ДС/|//0 = (С„Д4Э) |Д£/|//0. (4.274)
Если емкость ФП является накопителем, ТО время Тн max не зависит от площади элемента Аэ. Расчет значений Гитах для *^К ФПУ спектральных диапазонов III—IV представлен в табл. 4.2. Расчет проведен для угла зрения +40° и типовых значений параметров = 0,5; Д £7 = 5... 10 В; Сн/Аэ= (3 . .. 5) *
|
Спектральный диапазон
|
• 10-8 ф/см; CnMJ/Аэ^З-10-7 Кл. Снижение допустимого времени накопления из-за тока теплового излучения заметно уже в спектральном диапазоне 3 ... 5 мкм и становится особенно существенным в диапазоне 8 ... 14 мкм. При превышении времени Гитах ячейка «слепнет», в ПЗС изображение расплывается — избыточный заряд перетекает в соседние ячейки. Для устранения расплывания вводят специальные стоки для заряда — антиблюминги.
Для повышения времени Ти max ИЭДО СНИЖЭТЬ ТОК Iq, Т. е. применять те же меры, что и для улучшения радиационного порога (см. § 1.2 и 2,5). Когда эти меры исчерпаны (их возможности ограничиваются требованиями к оптико-электронной системе В целом), то ДЛЯ дальнейшего повышения времени Т„max приходится использовать специальные устройства деления и вычитания заряда. В ПЗС для осуществления деления в ячейку Кроме ОСНОВНОЙ емкости Сн ВВОДЯТ емкость Сст = &СН) как в схеме неполного слива (рис. 4.36,а), а также третью емкость — оконечный накопитель СИ2~Сц. Периодически, через время «Сентах, накопленный на основной емкости максимальный заряд Qн делят, его k-ю часть сначала передают на емкость Ссг (4.267), а оттуда — в оконечный накопитель СН2. Основную емкость Сн очищают для следующего подкадра (в отличие от рассмотренного ранее метода неполного слива). В результате в оконечном накопителе накапливается заряд kQ0 = klQT„, поэтому время Тн тах увеличивается в 1 jk раз. Если при этом на основную емкость Сн подать напряжение, превышающее напряжение на емкости стока на [Д{7|, то на основной емкости останется заряд Qn0CT = Сн | AU. Операция вычитания осуществлена: в сток стекает заряд Q—Qnoc-r, если k=l, а если k<ZU т0 часть заряда k(Q—Qn0cT), и тогда вычитание сочетается с делением.
К сожалению, при введении устройств антиблюминга, деления^ и вычитания теряется одно из самых привлекательных свойств накопительной ячейки — ее простота. Антиблюмингу необходимо предоставлять отдельную площадь, поэтому фоточув - ствительному элементу в двухмерных матрицах придется сильно потесниться. Из-за снижения коэффициента использования
Площади ячейки падает чувствительность, а зачастую необходимой площади просто-напросто нет. Возникают шумы Деления КТС-шум, сказывается разброс поверхностного потенциала* Все это ограничивает возможность перечисленных схемотехнических приемов.
Шумы при коммутации, В ПЗС заряд, накопленный в одной ячейке, сливается в соседнюю ячейку практически полностью. В других случаях в плавающей диффузионной области ПЗС, ячейках типа фотоприемники—ключ емкость полностью не разряжается, с помощью ключа устанавливается ее исходное состояние— потенциал и»сх и заряд Яясх= Сни„сх (рис. 4.37, а). В отсутствие тока ФП, т. е. при темновом кадре, это состояние должно сохраняться все время постоянным. При накоплении ток ФП разряжает емкость на {1<з^г^с.)Ты (ср. с рис. 4.37, в, д). Поэтому информативный заряд (^о+^с) 7„ приходится регистрировать относительно постоянного уровня Сниксх. К сожалению, этот уровень не является строго постоянным^ изменяется после каждой коммутации ключа. Флуктуации Д£ЯИСХ объясняются тем, что ключ подключает к емкости Сн не только генератор постоянного напряжения £/цСХ, но и генератор теплового шума еш2 = 4кТЯ, где И — сопротивление самого ключа и токопроводящей цепи (рис. 4,37,6). На низких частотах шумовое напряжение еш2 полностью падает на емкости, а на высоких —
|
Ав. |
|
Рис. 4.37. Тепловой шум сопротивления ключа и цепи приводит к флуктуации Устанавливаемого на ем - . кости напряжения и заря-.л ' Да (к КТС-шуму); |
|
11 |
|
О Л |
|
Йш № |
|
I Я!<Ь, |
|
А Установка напряжения ключом; б — эквивалентная схема при замкнутом, ключе; в — (изложение ключа; г — заряд на емкости {/о=0); д — заряд на емкости (/аг^О) |
|
Ік. |
|
В) |
|
») |
|
Оажг (3) |
|
Є-.Р) |
|
Я Си |
|
-ф- 6) |
 |
|
|
|
|
|
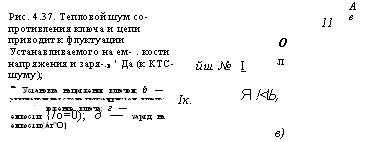 |
На сопротивлении Я. Для такого однозвенного фильтра с постоянной времени Тф = /?СН характеристическая шумовая полоса равна 1/4тф (табл. 4.1), поэтому дисперсия шума
=7ш/шб=4&77?/4/?С„ = й7’/Сн, (4.275)
АО!1 = Сн2д17^ = АГСн. (4.276)
Этот шум случайной установки потенциала (и заряда) так и
Называют КТ С-шум. Формулы выведены для стационарной модели. Но они остаются справедливыми и в динамике, если, конечно, емкость подключается к источнику напряжения на достаточно большое время (по сравнению с постоянной времени цепи Тф = /?СН). Интересно, что от сопротивления дисперсии
Д^исх> ЛС^сх не зависят, а зависал^ только спектр шума. С ростом спектральная плотность растет на низких
Частотах, зато полоса /ш. бпадает, поэтому мощность ^ш/ш. б остается постоянной. При разомкнутом ключе его
Сопротивление стремится к бесконечности, мощность шума сосредоточена вблизи нулевой частоты, поэтому в течение времени 7Н состояние накопителя не флуктуирует.
При низком уровне фона КТС-шума может ограничивать минимальную величину обнаруживаемого сигнала. При типовых значениях емкости Сн = 3-10-13 Ф (4,271) и рабочих температурах 77 . . . 300 К КТС-шум не позволит зарегистрировать число электронов меньше чем
=VДо!^/?=V кТс7/Ч=
= у (0,006 ... 0,026) 3-10^3/1,6-10-» « 100 ... 200. (4.277)
Можно ли устранить КТС-шум? Все зависит от способа отсчета и обработки этих отсчетов (рис. 4.37, г, д). На этих рисунках показаны три выборки: в начале кадра Q(l) = Q[^cx (1)> в конце кадра <2 (2), а также в начале следующего кадра <2(3) =(2 исх(З). Манипулируя указанными выборками, можно найти искомый информативный заряд Оо по крайней мере тремя способами.
Первый, самый непосредственный способ: используем только одну выборку в конце кадра ф (2). Чтобы определить информативный заряд (Зо, надо вычесть во внешнем устройстве средний уровень установившегося заряда фНсх
<? (2)- <?„„ = !<?„„ (2) - <?„] - = [<эйсх (2) - 0И„1 - С?0.
Недостатки такого способа очевидны. Во внешнем устройстве приходится предварительно формировать значения <2Исх для каждой ячейки, усредняя фИсх по многим выборкам в отсутствие сигнала, затем запоминать все значения фисх (ведь в многоэлементных ФПУ для каждой ячейки может быть свое значение С? исх) > Как видно из последней записи, флуктуации £всх (2), относительно своего среднего (т. е. КТС-шумы) в этом методе, к сожалению, не устраняются.
Второй способ — вычитание двух соседних выборок <3 (2)
Я 0(3):
(3 (3)—С? (2) — С^исх (3) [фисх (2) <Зо] =
[фисх (3)—Рисх (2)]Н-Ро-
Внешней системе обработки сигналов стало легче; ей не надо формировать значения Оисх и, главное, не надо запоминать матрицу этих значений 5Исх. Но теперь стали регистрировать флуктуации двух выборок <ЗИСх (3) и <3исх(2), так что мощность КТС-шума удвоилась.
И третий способ, в котором наконец-таки удается устранить КТС-шум, — это вычитание выборок 1 и 2, между которыми ключ не замыкался, а происходило только накопление (или передача в результате зарядовой связи) заряда <2о - Такой метод называется двойной коррелированной выборкой (ДКВ): двойной, потому что берут две выборки; коррелированной, потому что уровень установки (2Исх между этими выборками не меняется, так что эти выборки в темноте полностью коррели - рованы: @исх (1) =<3ИСХ (2) (рис. 4.37, г).
При большом фоновом заряде КТС-шум тонет в дробовых шумах этого фона. Формулы (4.235), (4.276) легко позволяют найти этот режим по напряжению перезарядки накопителя из-за этого фона Д£/ = /о71„/Сн:
Д<2исх.
ДОо"2=|?(Зо = ?СяД(7 > А7С„; и>кТ/ц = <(,. (4.278)
Таким образом, если накопитель перезаряжается током на несколько тепловых потенциалов, что наблюдаем в ИК ФПУ уже при временах Тп~ 0,1 Тн тах, то КТС-шум вообще можно не учитывать.
Труднее бороться с наводками от управляющих импульсов. При коммутации через накопительную емкость и сигнальные шины могут течь токи зарядки и разрядки паразитной емкости ключа Ск (рис. 4.37, а), возникают паразитные импульсы за счет переходных емкостей. Напряжения управляющих импульсов порядка или несколько выше напряжений перезарядки емкости при накоплении фоновых токов (около 2...20 В), стало быть, в 3000 и более раз превышает пороговые сигналы. При малом фоне это соотношение еще выше. Понятно, какие жесткие требования предъявляются к подавлению коммутационных помех, если необходимо обнаружить сигналы на уровне собственных шумов. Для снижения уровня помех вводят экранирующие электроды между тактовыми и сигнальными шинами,, коррелированные выборки берут при одинаковых потенциалах на управляющих шинах, сглаживают фронты тактовых импульсов и ограничивают их амплитуду; увеличивая время опроса, берут выборки установившихся значений, Если между опросами ячейки ФП-ключ ключ замыкают (выборки 1, 3 на рис. 4.37,д), то импульсы перезарядки паразитной емкости ключа устраняют, используя в выходном устройстве интегратор. Поскольку токи зарядки и разрядки емкости ключа переносят одинаковые заряды и текут в противоположных направлениях, то при интегрировании они взаимно уничтожаются.
Следовательно, при коммутации обработка и регистрация слабых сигналов усложняются. Хотя ее помехи принципиально устранимы, .но в реальных системах могут заметно ухудшать обнаружительные характеристики и всегда требуют к себе внимания и деликатного обращения.
Подведем итог. Основу накопительной ячейки составляет минимум функциональных элементов: ФП — емкость — ключ.
Если форма входного сигнала прямоугольная, шумы белые, время накопления 7’„ = ГС, а выборки синхронизированы с началом и концом сигнала, то в этом случае ячейка является оптимальным фильтром. Но и при отступлении от перечисленных условий потери в отношении сигнал-шум относительно невелики: при колоколообразной форме сигнала около 5%, небелом шуме (вида 1//) и использовании вычитания кадров около 26%. Заметнее потери из-за асиихронности опроса, в худшем случае они могут достигать 42 ... 50% (когда сигнальный заряд делится пополам между соседними кадрами). Снизить эти потери до 5... 10%, увеличить частоту опроса при сохранении необходимого времени накопления (а это позволяет также повысить точность измерения временного положения сигнала) можно при усовершенствованных методах обработки сигналов. В одном из таких методов— сложении лодкадров — необходимый интервал накопления Тк~Тс разбивается на п подкадров Гн/ = 7тц/п, причем достаточно выбрать £2^3... 5. Затем с периодом Т/ во внешнем процессоре рассчитывается сумма зарядов, накопленных в последовательности этих п подкадров. В другом методе неполного слива с емкости сливается и регистрируется на выходе только (1/га)-я часть накопленного заряда. Слив осуществляют достаточно часто, через те же интервалы Тя! п.
Следовательно, накопительная ячейка в общем случае является квази - оптимальным фильтром, обработка сигнала в ней аналогична обработке сигнала в традиционном ФПУ с усилителем и последующим коммгтатором. Именно это замечательное свойство накопительной ячейки выполнять почти оптимальную обработку сигнала наряду с удивительной простотой и сделало ее основным строительным материалом практически всех современных ФПУ — формирователей сигналов изображения (ФПУ-ФСИ), а в двухмер* ных ФГО-ФСИ при числе элементов свыше 10а... 104 — практически безальтернативным строительным материалом.