Фотоприемные устройства и ПЗС. Обнаружение сла­бых оптических сигналов

Сигнал и шум фотоприемных устройств ИМПУЛЬСНЫЙ ОПТИЧЕСКИЙ СИГНАЛ

Типовая форма, оптического сигнала. Задача обнаружения сигнала определена, когда заданы его отличительные призна­ки, по которым можно отличить сигнал от помехи. Как отмеча­лось в § 1.1, в большинстве оптико-электронных систем оптиче­ский сигнал является импульсным. Введем для него следующее обозначение:

£с(0=£сАес(*)’ (2.1)

Здесь £са — амплитуда сигнала (импульсная мощность оптиче­ского излучения, падающего на фоточувствительную площад­ку); МО—относительная форма импульсного сигнала (без­размерная величина). В некоторый момент времени t = t0 сиг­нал достигает своего максимального значения: £с(^о)~£са,

£с(^о) = 1- Относительная форма ес(0 и является отличитель­ным признаком сигнала.

В лазерных системах форма сигнала ес определяется кон­струкцией лазера (светодиода) и способом его возбуждения, а в сканирующих системах — распределением энергии в пятне и соотношением его диаметра с шириной площадки либо шири­ной щели механического модулятора. Простейшей формой сиг­нала является прямоугольная (рис. 2.1,а):

Е^=Х' (2.2) ес(С)=0.

На практике она может реализоваться при питании лазера (светодиода) импульсом тока прямоугольной формы, а в меха­нических системах — при диаметре оптического пятна много меньше фоточувствительной площадки либо щели модулятора. Однако в высокочастотных лазерных системах, когда стремятся получить максимальное быстродействие, сразу по достижении сигналом максимума ток накачки отключают, так что он начи­нает спадать — форма сигнала получается колоколообразной. Колоколообразным получается сигнал и в механических систе­мах, когда минимизируют размеры площадки ФЧЭ либо щели модулятора — выбирают их порядка диаметра пятна. Обычно такой импульс описывают косинусквадратной функцией [1, 4] (рис. 2.1,6):

-ГС<<<ГС, ес(() = С05*-%-^--,

*<ГС, (>Тй, ес(*)=0. <2-3)

Как правило, нет необходимости детализировать форму пятна. Необходимость более строгого расчета формы сигнала может

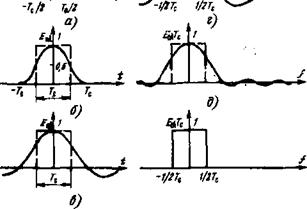
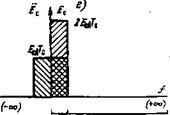
Рис. 2.1. Аппроксимация прямоуголь­ником оптических сигналов и их спектров

Возникнуть в другой задаче — при распознавании отличных друг от друга, более сложных по форме сигналов. Мы рассмат­риваем оптико-электронные системы, предназначенные для об­наружения, когда возможны лишь две ситуации — сигнал есть либо его нет. При обнаружении прежде всего важны два па­раметра сигнала — его амплитуда £са и эффективная длитель­ность Тс. Чем сильнее сигнал £са, чем точнее можно подстро­ить полосу фильтра под его эффективную длительность, тем больший сигнал можно получить на выходе фильтра-усилите­ля, тем меньше вероятность спутать его с помехой. Мелкие детали формы импульса при настройке фильтра оказываются несущественными (§ 3.3). На этом основании можно упростить наш анализ и в первом приближении даже не рассматривать конкретную форму фронтов импульсов — аппроксимировать ре­альный колоколообразный импульс прямоугольным. При такой аппроксимации надо, конечно, проследить, чтобы сохранились
мощность (амплитуда) и оптическая энергия (площадь) им­пульса (рис.'2.1, б):

Оо со

ТсЕСА= jj EzKez{t)dU тс= ^e<L{t)dt. (2.4)

—00 —оо

За эффективную длительность реального колоколообразного импульса ez(t) и следует принять величину Тс, т. е. его пло­щадь (2.4). Для косинусквадратного импульса (2.3) его дли­тельность по уровню 0,5 от амплитуды будет в точности равна эффективной деятельности (2.4), поэтому для этих длительно­стей и введено единое обозначение 7V

Спектр оптического сигнала. Любой сигнал можно предста­вить в виде суммы гармоник Јc(f)cos (2л//4"^с) [50, 51]. Функ­ции £с(И, фс(Н являются амплитудой и фазой спектра сигна­ла; частота изменяется во всем диапазоне значений, f=[—оо, оо]. Поскольку рассмотренные оптические импульсы симмет­ричны относительно точки отсчета t — tQ = 0 (рис. 2.1 ,а, б), то в их спектре содержатся только четные гармоники — косинусоиды и ^с = 0. В этом случае обратное и прямое фурье-преобразова - ния, связывающие импульс Ec(t) с его спектром Ec{f), имеют соответственно вид

Со

Ес (t) jj Ёc(f) cos 2лf tdt, (2.5)

—оо оо

Ёс(/) = ^ Ec(t) cos 2nftdt. (2.6)

—оо

Так как косинусоиды на положительных и отрицательных ча­стотах неразличимы, cos2jt(—f) Tc = cos 2nfTc, и согласно (2.6) спектральные плотности для симметричного импульса одинако­вы, £с(—f)E=Јc(f), то эти гармоники складываются:

Ёс (— /) соs 2л (— /) Тс+Ёс (f) cos 2л f Тс ^

= 2Ec{f) cos 2я/Гс. (2.7)

По этой причине часто оперируют только положительными ча­стотами; для этих частот определяют коэффициент передачи усилителя K(f), вводят спектр сигнала:

/ = |0, со], £с(/) = 2£с(/). (2.8)

В настоящей книге удобно будет использовать как спектр Јc(f) При разложении в диапазоне частот f — [—оо, оо], так и спектр удвоенной мощности Ec(f) при разложении по гармони­кам только положительных частот / = [0, оо].

Из прямого и обратного

Фурье-преобразований (2.5), (2.6) следуют три общие за - г,2 ( кономерности, справедливые с - для спектра симметричного импульса произвольной фор - мы.

Первая закономерность. ^Характеристической частотой :! спектра импульса является частота 1/2 Тс: в окрестностях этой частоты начинается спад спектральной плотности. Осо­бенно легко прослеживается

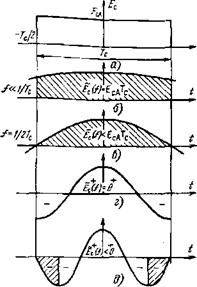
Рис. 2.2. Спектральная плотность £с прямоугольного импульса опреде­ляется площадью косинусоиды на ин­тервале Тс:

А ~ форма импульса; 6—низкая частота; в — граничная частота; г, д — высокие частоты

Эта закономерность на примере прямоугольного ^шпульса (рис. 2.2, а). Согласно (2.6)спектральная плотность Ес в этом случае равна площади (интегралу) косинусоиды на интервале Тс, а на низких частотах [<С1/2Гс и косинусоида, и интеграл от нее постоянны (рис. 2.2,6). Лишь когда полупериод 1/2/ становится равным (примерно равным) длительности импуль­са, площадь косинусоиды уменьшается (рис. 2.2, в). На высо­ких частотах /^>1/27с, когда в отрезке Тс укладывается не­сколько полупериодов косинусоиды, спектральная плотность резко уменьшается и может стать равной нулю (рис. 2.2, г) либо отрицательной (рис. 2.2, д).

Вторая закономерность. Спектральная плотность Ес на низких частотах /<С1/2Гс равна энергии (площади) оптическо­го импульса. Это непосредственно следует из формулы фурье- преобразования (2.6), если положить в ней соз2л;^ = 1, по­скольку 2 л;//да 0:

(2.9)

V. . (2.10)

Здесь мы воспользовались определением эффективной длитель­ности (2.4). Поскольку для рассматриваемых импульсов спек­тральная плотность Яс(/) максимальна на низких частотах и
всегда равна £са^с, то удобно эту плотность (2.9) пронормиро­вать к указанному значению (а спектр Ес(П отнести к величи­не 2ЕсаТс) и ввести относительный безразмерный спектр ес(/):

Ес (/) —ЕсаТСес (/), Ес (/) = 2ЕсаТ с^с (?) >

Где £<:(/) ~'7^Г ^ Єс(£)С0^2п/І(ІЇ.

Из приведенного определения ес(/) следует, что на нулевой частоте необходимо получить ес(0) = 1. Это подтверждают и выражения (2.4), (2.11).

Третья закономерность. Площадь спектра равна амплитуде сигнала. Своего амплитудного значения импульс достигает в момент £=0, поэтому из обратного фурье-преобразования для этого момента следует, что

£^ = £«,(0 )=$ (/)£*/• .■■■■> ~ . ... (2.12)

Физически это очевидно: в момент /=0 гармоники всех частот достигают своего амплитудного значения Ёс([) и складываются, давая в сумме амплитуду сигнала £сА. Обе последние законо­мерности были доказаны идентичными методами: в (2.5), (2.6) полагали со5 2л/^=1 (соответственно считая /-»-0 либо £=0).

Теперь рассчитаем конкретные спектры для рассмотренных выше импульсов. ,

Импульс прямоугольной формы

(2.13)

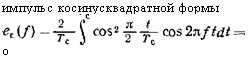5ІП 2Я/Ге

___ 1 е________ (П 1 ДЧ

Гя/ГсП—(2/7-с)1

Эти спектры представлены на рис. 2.1, д. Для косинусквад - ратного импульса ес(0 была введена простая (прямоугольная) аппроксимация. Теперь такая же (по форме) аппроксимация «напрашивается» и для частотной характеристики ес(1). Заме­ним реальный спектр ес(1) прямоугольным — с постоянной

Плотностью ЕсаТъу ес= 1 в интервале частот 0..Л/2 Тс (рис. 2.1, г, д). Так можно ввести эффективную полосу сигна­ла /с:

(2.15)

Эта формула является следствием (2.10), (2.12). И для точно­го спектра, и для аппроксимации выполняются все три обяза­тельных условия: спектральная плотность на низких частотах Ес. есть площадь (энергия) оптического импульса ЕсАТс, пло­щадь спектра есть амплитуда 2(£сД7с) (1/2Гс) =ЯсЛ, спад про - исходит на частоте (в окрестностях частоты) 1/2Тс. Конечно, предложенная прямоугольная аппроксимация спектра не есть спектр прямоугольного импульса. С помощью обратного фурье- преобразования можно найти точную временную форму им­пульса, соответствующего этому спектру:

(2.16)

Зеркальность прямого и обратного фурье-преобразований при­водит и к зеркальности формы функций ec(t) и ec(f) пря­моугольной форме импульса ec(t) соответствует спектр вида ес(П '»Sin х/х (2.13) (рис. 2.1, а, г) и, наоборот, прямоугольно­му спектру ec(f) соответствует форма импульса вида ес(0 <х> sin х/х (2.16) (рис. 2.1,6, г).

Таким образом, и сам колоколообразный сигнал ec{t), и его спектр ec(f) аппроксимировали прямоугольниками (рис. 2.1). Такое «прямоугольное мышление» лежит в основе одного из главных методических приемов настоящей книги. Выполняя все конкретные расчеты для этих аппроксимаций, «на пальцах» выведем основные законы теории обнаружения, получим о них наглядное физическое представление. Конечно, строгими такие расчеты будут соответственно для прямоугольного импульса и формы импульса вида sin х/х. Но весь смысл методики заклю­чается в том, что получаемые для этих импульсов закономер­ности можно в первом приближении распространить на все семейство колоколообразных импульсов. Ведь основная доля энергии оптического сигнала сосредоточена на временном от­резке Тс (в диапазоне частот 0... 1/2 7^). Форма фронтов им­пульса (форма спада относительного спектра в окрестности ча­стот /со 1 /27' с) влияет на эффекты второго порядка

Асимметричные импульсы. Ра­ди общности анализа рассмотрим последовательно три более слож­ные ситуации, когда симметричное расположение импульса относи­тельно начала отсчета времени /=0 нарушается.

Пусть форма импульса остается симметричной, но он сдвинут отно­сительно начала отсчета на отре­зок и (рис. 2.3, а). Тогда запись для формы такого импульса ес(0 и его спектральных составляющих модифицируется:

Ес (()-+ес (£—М >

£сС05 2я/(*—*„)=" (2.17)

—Ес (!) соз (2я^—2я^0). т. е. фаза стала отличной от нуля, ~

—2я//0-

Пусть теперь асимметрично не положение, а сама форма импуль­са (рис. 2.3,6). Поскольку чет­ность импульса нарушена,

Ес{—ЦФЕс(/), то в спектральном разложении обязаны по­явиться нечетные слагаемые — синусоиды, следовательно, фазо­вая характеристика также станет отличной от нуля.

В этом случае в (2.5) надо ввести фазу:

£С(0= 5 ^с(/)СОЗ(2л/7 + 11)с)<*/.

Две первые закономерности, полученные для симметричной формы импульса, здесь сохраняются. Как видно из рис. 2.2, до­казательство спада спектра на частоте около 1/2 Тс не требо­вало от импульса его обязательной симметрии. При расчете спектральной плотности на нулевой частоте Ес(0)—Е^АТС по­лагали со5 2л//=1. Но на нулевой частоте даже для асимме­тричного импульса ■фс^О, так что 2я/Н-фс—0, соз(2я/7+.^с) = 1, поэтому формула (2.9) и осталась справедливой. Однако третья закономерность нарушается: амплитуда импульса не равна площади амплитудного спектра. Согласно (2.18) надо учиты­вать и фазовую характеристику:

СО

ЕсА=Ес(0)= ^ Яс(/)соефс(/)<//.

—со

Еще сложнее связь амплитуды импульса Еса с его спект­ром для третьего, последнего примера, который здесь рассмот­рим, — скачкообразного импульса (рис. 2.3, в). В этом случае в точке /=0 имеется неопределенность: значение Е0{1) ме­няется скачком от нуля до £сд> поэтому расчет по (2.19) дает среднее значение ЕсА/2. Если нам известен спектр, то для нахождения амплитуды Еса в этом случае надо пользоваться общей формулой (2.18), получить сначала временную зависи­мость ЕсЦ) и устремить (-+0 справа.

Все три приведенных импульса можно по прежней методике аппроксимировать прямоугольным импульсом, приравнивая их амплитуды и площади (рис. 2.3). В свою очередь, и спектр та­кого прямоугольного импульса можно аппроксимировать пря­моугольным— с постоянной плотностью Е0=ЕсАТс в диапазоне частот [—1/27’с, 1/2Тс]. Но, как было уже показано (2.19), площадь такого спектра 2(£’сЛ) (/2Тс) =ЕсА в общем случае не равна площади реального амплитудного спектра асимметрич­ного импульса.

Подведем итог. Типичный оптический сигнал, регистрируемый ФПУ,— импульсный, колоколообраэной (косинусквадратной) формы. Для дальней­шего его анализа достаточно ввести в рассмотрение всего два параметра импульса: амплитуду ЕСь и эффективную длительность Тс. Спектр оптическо­го импульса можно в первом приближении считать постоянным в полосе частот—1/2 Тс, 1/2 Гс> имеющим плотность в этой полосе Ес=ЕсЛкТс (или - Ес — 2ЕсаТс в полосе 0...1/2 7’с). Такая простая аппроксимация является важным методическим приемом и позволяет легко проследить физику всех операций обработки сигнала при его обнаружении, не теряя при этом общ­ности анализа.