Фотоприемные устройства и ПЗС. Обнаружение слабых оптических сигналов
ШУМЫ ФОТОПРИЕМНИКА
В предыдущем параграфе были получены общие представления о природе шумов в ФП и их статистических характеристиках. Теперь перейдем к выводу выражений, с помощью которых можно количественно рассчитать спектральную плотность шума ФП по его известным фотоэлектрическим параметрам.
Шум ФД представляет собой хаотическое наложение импульсов, наведенных каждым носителем заряда в отдельности (§ 2.2). Пусть на интервале наблюдения Т приходит один электрон. Он индуцирует в цепи ФД импульс тока длительности Тцрол■ Площадь такого одиночного импульса тока равна переносимому заряду, т. е. заряду электрона ц. Поскольку наведенные ИМПуЛЬСЫ ОЧеНЬ КОрОТКИе Тпрол ~ (10 '11... 10~8) с (§ 1-2), то завал спектра начинается на очень высоких частотах (§ 2.1)
1/2тщх>л= 1/2(10~11... 10-8) -5(107... 1010) Гц. (2.73)
В физике вводится понятие дельта-импульса 5 (*—*0) — бесконечно короткого импульса бесконечной амплитуды [52]. Иначе говоря, этот импульс равен нулю, за исключением момента 1=и, когда его значение стремится к бесконечности. Реально «бесконечно короткий» — значит короче всех других характеристических времен (времени наблюдения, постоянной времени радиотракта). Следовательно, спад в спектре импульса, кото» рый считаем дельта-импульсом, должен начинаться выше рабочих частот (как это имеет место в ФПУ с ФД). Количественная характеристика дельта-импульса — не амплитуда и не средняя длительность, а площадь, которая по определению принимается равной единице:
Оо
^ б (*-*«)<#= 1. (2.74)
—оо
Тогда импульс тока записывается следующим образом:
1(0 = д6 (*—*„). (2.75)
Как видим, шумовые импульсы тока ФД можно рассматривать как дельтаобразные импульсы, характеризовать их площадью— зарядом д. Спектр такого одиночного импульса в рабочей полосе частот не зависит от частоты; такой спектр называют белым. Его плотность /(/) согласно § 2.1 равна удвоенной площади импульса:
1(0=2д. (2.76)
Амплитудный спектр одноэлектронного импульса оказывается детерминированным, однако фаза, определяемая случайным положением импульса и на интервале наблюдения, случайна. Как было показано в предыдущем параграфе, в этом случае следует вводить спектральную плотность мощности шума, которая согласно определению связана со спектром реализации (2.76) соотношением (2.35):
/2 (/) = /2(/)/2Г - {2д)Ч2Т ^2<р1 Т. (2.77)
Пусть теперь за время наблюдения Т в данной п реализации пришло Л^п носителей заряда. Полный ток есть сумма токовых импульсов, индуцированных каждым носителем, и средний ток за время Т в п реализации
1^дЫп/Т. (2.78)
Поскольку дисперсия суммы равна сумме дисперсий Ып независимых слагаемых (а импульсы независимы — независимы моменты их прихода ^o), то спектральная плотность возрастает в данной реализации в кп раз:
Здесь ток в п реализации /п заменен на средний ток 10> что справедливо при Т-+-оо.
Полученное выражение — это известная формула Шотки для дробового шума, одно из основных выражений статистической радиотехники [56, 60]. Оно справедливо для фотодиодного режима, когда ток /0 есть обратный ток ФД /=/о» обусловленный термо - и фотогенерацией. При малом обратном смещении и особенно при прямых смещениях становится существен также прямой ток /тгехр (£//<рт) (см. (1.37)). Прямой и обратный (1.38) токи статистически независимы, так что мощности этих шумов складываются [60];
Л(/) =2^/0+2^/тгехр(С//фт). (2.80)
Когда прямой и обратные токи взаимно уравновешиваются, то это выражение упрощается:
2q/0 = 2qIJrexp(U/%), J2 (/) = 4qlтг exp (U/<рт) =
= 4kT (q/rcJkT)exp(Ulq>T) = 4kT }#ф. (2.81)
Здесь была использована формула для динамического сопротивления ФД (1.62). Отметим, что при наличии фоновой генерации (/тф+/фф^0) данный режим реализуется при холостом ходе, Нф = /?ф хх (1.64). Когда же фоновой генерации нет (h = = /тг, 0), то прямая и обратная составляющие тока термо
Генерации уравновешивают друг друга и при коротком замыкании /?ф из/?ф (1.63).
Как будет показано ниже, формула (2.81) представляет собой выражение теплового шума сопротивления /?ф. Так два основных механизма (дробовой и тепловой) в частном случае приводят к одному выражению для спектральной плотности мощности шума.
Шум лавинного ФД. Пусть теперь каждый входящий в ОПЗ носитель умножается точно в М раз. Переносимый заряд (площадь элементарного импульса) соответственно увеличивается в те же М раз. Поэтому в те же М раз увеличивается спектральная плотность одиночного импульса, /(f) = 2qM, а спектр шумов как квадрат спектра импульса возрастает в М2 раз. Тогда по аналогии с (2.77) — (2.79) получаем
J4f)=T^ ~ = TNn =
= 2qlp-M>=2qll>M2. (2.82)
Однако умножение также является случайным процессом: для всех N первичных носителей имеем N случайных значений коэффициента умножения ММ2,.. г, Ми..., Поэтому выражение (2.82) уточняется:
(2.83)
Г—1 *=1 /
Выражение для шума ЛФД можно было получить и из его эквивалентного представления схемой рис. 1.9, я. Вторичный ток больше первичного в М, раз, а при умножении на константу дисперсия умножается на квадрат константы М{. Усредняя ло реализациям с разными МД также придем к формуле (2.83).
Флуктуация умножения привела к дополнительному шуму (значение среднего квадрата М2 больше квадрата среднего М2). Этот шум называют избыточным шумом лавины (не путать с избыточным фликкер-шумом со спектром вида 1//, см. § 2.4). Формулу (2.83) представляют в следующей форме [61—63]:
7Ц/) = 2дШ2Р, (2.84)
Здесь Т7 — шум-фактор, показывающий, во сколько раз мощность шума реальных ЛФД выше мощности шума гипотетического идеального умножителя с постоянным (нешумящим) значением М{ = М. Для расчета шум-фактора надо знать функцию распределения коэффициента умножения М{. Соответствующие расчеты приводят к выражениям [63]:
|
Р = Ш+{2~1М){-ку, |
(2.85) |
|
Л1>> 1, Р = + 2(1-А); |
(2.86) |
|
Ж>1, £^0(УШ<1), Р = 2; |
(2.87) |
|
УИ>1, г = |
(2.88) |
|
Как видно, шумы лавины сильно зависят |
От отношения ко- |
Эффициентов ударной ионизации носителей Когда размножается только один тип носителей, например электроны (&-»-0), то развивается односторонняя лавина—в направлении движения электронов. Шумы такой лавины минимальны. Если наряду с электронами размножаются и дырки (£-*1), то генерированные в каждом акте ударной ионизации дырки при своем обратном движении возбуждают новую лавину. Возникает разветвленная лавина, в которой содержится в среднем М «ветвей». Мощности шума каждой «ветви» складываются, что приводит к наибольшему расшумливанию — вплоть до> М раз.
|
|
|
10 |
|
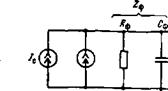
Рис. 2.11. Аппроксимация шум-фактора ЛФД—степенной функцией ( ) (а) и зависимость шумового коэффициента у, от отношения к (б) |
На рис. 2.11, а согласно (2.85) в двойном логарифмическом масштабе построена зависимость шум-фактора У7 от среднего коэффициента умножения М. Предпринята попытка аппроксимировать эту зависимость в диапазоне типовых значений М = = 10... 200 прямой, т. е. степенной функцией:
|
(2.89) |
![]() Р = МЛ.
Р = МЛ.
|
(2.90) |
![]() На рис. 2.11,6 приведены подобранные по такой методике значения шумового коэффициента х, которые являются функцией отношения коэффициентов ударной ионизации к. Значение у,{к) можно подобрать с точностью примерно 15% (в таких малых пределах оно зависит еще и от самой величины М). С учетом этой аппроксимации (2.89) выражение (2.84) для шумов ЛФД переписывается в следующей, самой распространенной форме:
На рис. 2.11,6 приведены подобранные по такой методике значения шумового коэффициента х, которые являются функцией отношения коэффициентов ударной ионизации к. Значение у,{к) можно подобрать с точностью примерно 15% (в таких малых пределах оно зависит еще и от самой величины М). С учетом этой аппроксимации (2.89) выражение (2.84) для шумов ЛФД переписывается в следующей, самой распространенной форме:
Л = 2д/М'
Кремний — основной полупроводниковый материал полупроводниковой электроники — и здесь не имеет себе равных. Для этого материала отношение к мало, порядка (1 ...5)-10-2 [38], поэтому мал и шумовой коэффициент х, порядка 0,2 ... 0,3 {рис. 2.11,6), что наряду с малыми темновыми токами (табл. 1.1) позволяет создавать на этом материале самые совершенные низкошумящие ЛФД. Структуры проектируются так (рис. 1.6,б, в), чтобы размножались фотоэлектроны, коэффициент ударной ионизации которых выше, чем у дырок.
Однако кремниевые ЛФД чувствительны до длин волн 1 ... . . . 1,1 мкм. На второй спектральный диапазон (длины волн 1,3 и 1,55 мкм) в интересах ВОСП разработаны ЛФД на ос
нове германия, тройных соединений Оа1пАз—1пр (последний материал обеспечивает меньшую плотность темнового тока ФД — порядка Ю“8 А/мм2 по сравнению с 10~6 А/мм2 у ФД на основе германия). Недостаток этих материалов — близкое значение коэффициента ударной ионизации электрона а и дырки р (* = 0,5). Поэтому одно из основных направлений развития фотоэлектроники за последнее десятилетие •— поиск полупроводниковых соединений и структур с малым отношением 6. Поиск ведется в направлений синтеза материалов с требуемой зонной структурой (показано, что при так называемом резонансе в валентной зоне р>а); в направлении создания канальных структур, где один из носителей выносится из области размножения; в направлении создания варизонных структур и структур со скачком потенциала в зонах, в которых необходимую для ударной ионизации энергию набирает преимущественно один тип носителей [38].
Шумы ФР находятся по аналогии с шумами ЛФД. В ЛФД в М раз увеличивается амплитуда элементарного импульса, а в ФР в тж/тпрол раз возрастает его длительность (§ 1.2). Но, главное, в обоих случаях увеличивается переносимый элементарным импульсом заряд (площадь импульса) — он соответственно равен Л1<7 и (тж/тпрол)Поэтому и выражения для спектра шума этих приборов идентичны: в формулу для ЛФД
(2.83) входит средний квадрат его усиления М2; Теперь егО надо заменить на средний квадрат усиления ФР (тж/тпрол)2:
-2 —2 . Т„
Л (/) = 2Д! - 2= 4д1 (2.91)
*прол / тпрол тцрол
Здесь, как и в ЛФД, введен шум-фактор /?==^/(тж)2 и использовано его значение Р=2. Это точно такое же значение шум - фактора, как и в ЛФД, в котором ионизирует лишь один носитель (& = ()) (2.87). Такое совпадение не случайно: и коэффициент умножения такого ЛФД, и время жизни ФР подчиняются одному (экспоненциальному) закону распределения. Читатель с помощью (2.84) может проверить, что при таком законе шум-фактор действительно равен двум.
Дополнительное усиление не дается даром: из-за его избыточных шумов не только ЛФД, но и ФР_уступает ФД по собственному отношению сигнал-шум (в У Р раз). Внутреннее усиление становится полезным при заметных шумах усилителя (§ 1.2, 2.5).
Выражение для шума ФР можно получить и другим методом— с помощью эквивалентной схемы рис. 1.8, а (подобно методике, использовавшейся при расчете шумов ЛФД). Не напрасно подчеркивалось, что в ФР есть два независимых дробовых процесса — генерация и рекомбинация. Каждый из них
Отражается на входе схемы генератором 2д/, так что общая мощность удваивается. На выходе мощность шума усиливается в Л2(/) раз, где Кф{!) — усиление ФР (1.14), (1.27):
|
(1 + со’т: |
|
.2 ' прол |
|
) ’ |
|
|
|
|
![]()
Формула (2.91) была получена для плотности шума на низких частотах и на этих частотах совпадает с последней (2.92), которая получена для всей области частот. Поскольку шумовые
ИМПУЛЬСЫ В ФР наМНОГО ДЛИННее, чем В ФД И ЛФД (Тж^Тдрол) > то приходится учитывать небелый характер шума — спад на частоте
/г=1/2дтж=1/2л:(10_6... 10~2) « 15 Гц...150 кГц. (2.93)
Шумы ПЗС-ячейки. Как было показано (см. § 1,1» 1.2), ПЗС-ячейка по физике работы аналогична ФД с тем отличием, что разделенные носители не уходят во внешнюю цепь, а накапливаются на емкости. Поэтому и шумы ПЗС-ячейки имеют такую же (дробовую) природу, что и фотодиода, — описываются генератором 2ці, подключенным к накопительной емкости.
Шумовая эквивалентная схема ФП. Проведенный анализ позволит дополнить обобщенную эквивалентную схему ФП генератором шумового тока (ср. рис. 1.8,6 и 2.12), представив этот генератор в следующем виде:
(2.94)
|
|
|
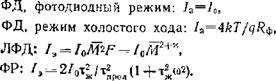
Ток 1Э называют током эквивалентного шумового диода. Этот термин понятен: любой источник шума Р можно заменить эквивалентным ему диодом с обратным током 1Э, рассчитанным ло (2.94); дробовый шум такого диода равен замещаемому.
|
|
Рис. 2.12. На эквивалентной
■° схеме фотоприемника шумы отражаются генератором 2д!3
Подведем ИТОГ. Импульсы тока от отдельных носителей в ФД можно считать бесконечно короткими, а их спектр — белым. Это обусловливает и белый характер шума ФД; плотность мощности шумов прн обратном смещении определяется известной формулой Шотки 2^/0, где /0—обратный ток ФД. В ФП с внутренним усилением Кф мощность шума возрастает больше чем в Кф2 раз, что вызвано флуктуацией самого усиления. Шум-фактор за счет флуктуации фоторезисторного усиления равен двум, а 33 счет флуктуации лавинного умножения либо двум (когда размножаются носители одного знака), либо коэффициенту умножения {такой максимально большой шум - фактор наблюдается при равенстве коэффициентов ударной ионизации электронов и дырок).