Фотоприемные устройства и ПЗС. Обнаружение слабых оптических сигналов
ОТНОШЕНИЕ СИГНАЛА К ШУМУ НА ВЫХОДЕ ОПТИМАЛЬНОГО ФИЛЬТРА (АНАЛИЗ В ЧАСТОТНОЙ ФОРМЕ)
Общее выражение для отношения сигнал-шум на выходе пл тимального фильтра. Формула для отношения сигнал-шум на выходе фильтра-усилителя с произвольной частотной хаоактепи-
Стикой была приведена в предыдущем параграфе (3 34)_______________
(3.36) . Там же была найдена и частотная характеристика оптимального фильтра (3.46). Подставляя последнюю из названных формул в первую, получаем искомое выражение:
<Х>
, 5/? „ о р 27"с kecdf
|
VI |
![]() ДГ°Ф сЛ с А 0
ДГ°Ф сЛ с А 0
£2Є4/
О
|
(3.48) |
![]()
|
У2?/и |
![]()
|
Д/ |
![]()
|
О |
![]()
![]()
|
0 |
![]() СА О
СА О
После сокращения приходим к выражению
О
Полученные выражения заслуживают короткого комментария-
1. Шумовая полоса оптимального фильтра совпадает с соб* ственной шумовой полосой усилителя с коэффициентом усиления & — ес/у 0 (такое усиление имеет второй каскад оптимального фильтра, рис. 3.7). Напомним, что шумовая полоса собственно усилителя, определяемая при белом входном шуме, равна площади под кривой к2:
ОО СО СО
2. Относительная амплитуда определяется той же полосой, точнее, ее отношением к эффективной полосе спектра сигнала
$с~1/2Тс:
Со
О
3. Метод фурье-анализа в линейных системах позволяет рассчитывать каждую гармонику и сигнала, и шума независимо друг от друга, а затем при расчете амплитуды сигнала и среднеквадратичного значения шума суммировать соответствующие гармоники. Оказывается, для расчета отношения ЛГС/Ш применим аналогичный метод. Сначала можно найти отношение сигнал-шум Пс/ш на входе фильтра для каждой из гармоник в отдельности. Максимум, что может оптимальный фильтр — «не навредить», бережно сохранить все эти парциальные отношения на выходе. Тогда значение Ыс/т находится геометрическим суммированием всех указанных парциальных отношений сигнал-шум — точно так, как это делается и для мощности сигнала, и для мощности шума. Действительно, на частоте I в единичной полосе амплитуда сигнала равна ЗБсА2Тсес(/), а среднеквадратичное значение шума ]/2^/ш©(/) , так что их отношение
Геометрическая сумма этих парциальных отношений совпадает с полученной выше формулой:
Приведенные выражения для принадлежат к числу фунда
Ментальных соотношений теории обнаружения. По определению полученное значение является максимально достижимым для отношения сигнал-шум при заданных спектрах и &(!)■
Пытаться получить отношение Л^/ш больше, чем в оптимальном фильтре, — все равно, что построить вечный двигатель. Значение Мс/Ш в реальных ФПУ может только приближаться к значению N сш < Продолжая проводить аналогию с двигателем, введем столь же важную характеристику, как и КПД, — коэффициент потерь (или просто потери) ФПУ (реального фильтра), который показывает, насколько отношение сигнал-шум в этом* устройстве меньше, чем в оптимальном:
П= ЛГс/ш/N с%1 • (3.54)
Коэффициент потерь является важнейшим показателем качества ФПУ как обнаружителя слабых оптических сигналов.
Расчет значения N1% для конкретных спектров сигнала и шума является одной из основных задач теории обнаружения. Поскольку формула для величины уже найдена, то даль
Нейший расчет сводится к обычным математическим вычислениям. Однако получаемые при этом формулы—в общем случае сложных спектров ес(/)> ©(/)—достаточно громоздки, при их выводе теряется физика оптимальной фильтрации. Чтобы избежать этого и проследить, как и почему отношение зависит от параметров сигнала и шума, воспользуемся сначала упрощенной методикой:
Будем непосредственно рассчитывать и сигнал 5Есис, и
Шум У 2геометрически как площадь под кривыми ес&, 0£2, а потом уже находить их отношение;
Будем следовать рекомендациям § 2.1 — проводить расчеты для эффективного прямоугольного спектра сигнала постоянной плотности 5£са23гс в полосе 1/2Тс;
Будем рассматривать «чистые» случаи, когда преобладает одна из компонент шума: белая, высокочастотная либо низкочастотная.
Конечно, надо помнить, что и сигнал 5£,с. амСа, и шум У2<7/ш/ш — величины относительные. Чтобы получить абсолютные напряжения на выходе ФПУ, надо умножить указанные значения на коэффициент передачи /Со (который в (3.48) сокращен). Поэтому, когда будем, например, говорить, что с ростом полосы фильтра сигнал растет, будем иметь в виду фильтры с одинаковыми значениями Ко - Поскольку величина в общем случае размерна (в нашем случае размерности сопротивления), то, опуская ее (точнее, полагая /Со = 1), изменяем также размерность относительных значений сигнала и шума на выходе фильтра. И все же в дальнейшем сохраним Для них условно обозначения напряжений Ос, V ш, понимая под ними безразмерные величины.
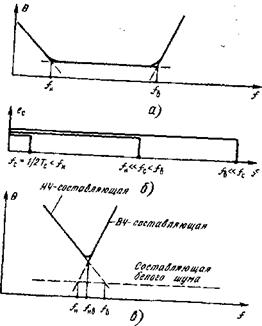
Расчет отношения N с? ш '• качественный анализ. Белый Щм. Спектры сигнала и шума приведены на рис. 3.8. Здесь же приведена частотная характеристика оптимального фильтра — в данном случае она воспроизводит прямоугольный спектр сигнала. При этом графический расчет сигнала и шума особенно Прост — соответствующие им площади на рисунке заштрихова - Как видно из рисунка, такой фильтр пропускает все гар-
|
№^уТс обеспечивается только при подстройке фильтра: для каждого значения Тс нужно устанавливать свою оптимальную полосу /у=1/2Гс. Высокочастотный шум. Этот случай иллюстрируется рис. 3.9. Сначала рассмотрим «чистый» ВЧ-шум (непрерывная кривая на рис. 3.9,6). Для простоты опять выбираем фильтр с |
|
Зивисимость вида |
|
V 2?/, Основная особенность полученного выражения—в корневой зависимости отношения Л^/ш от эффективной длительности сигнала Тс. Из выкладки понятна природа такой зависимости: амплитуда сигнала сохраняется постоянной при любой его длительности, а среднеквадратичное значение шума с ростом длительности падает из-за сужения полосы, поскольку для более длинного импульса Гс допустима меньшая полоса фильтра ({/„, «з У7~у ог у 1 /2 Тс). Конечно, |
|
Ж г оф ^ сА Л с /ш —• / 7 V ТТI |
|
'сА |
|
У2ТС. |
|
(3.57) |
|
Моники сигнала без потерь, поэтому амплитуда сигнала на выходе не снижается: А= (5Есд2Гс)/у= (ЭЕслЯТс) (1/2Гс) = 5£сА. Шум при выбранной полосе /у^/ш = /с равен |
|
£/ш=1/2?/ш/у =У257ЛТ/2Гс), Откуда искомое отношение |
|
'(3.55) (3.56) |
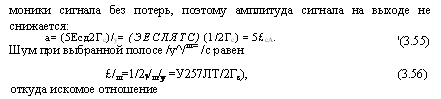 |
 |
 |
|
|
||
|
|
||
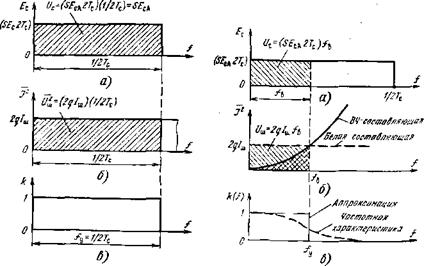
Прямоугольной частотной характеристикой £(/), но будем теперь варьировать его полосу ^ в диапазоне частот О—/с. Поскольку полоса усилителя становится уже полосы сигнала, то сигнал «зарезается» относительная амплитудная чувствительность меньше единицы и определяется отношением полос усилителя и сигнала:
С/са—5£,са«са=:5Яса.(/у/^с) = .(5£са2Тс)/у, (3.58)
Высокочастотный шум в этой полосе
^^ з7^* (3.59)
Площади, определяющие значения ис, С/ш, на рис. 3.9 также заштрихованы. Для отношения сигнал-шум получаем
Отсюда видно, что теоретически при бесконечно узкой полосе (/у-»-0) можно получить бесконечно большое отношение сигнал - шум. Это и понятно: на низких частотах плотность ВЧ-шума очень быстро стремится к нулю. Реальность вносит свои коррективы: наряду с ВЧ-составляющей необходимо учитывать и белый шум (штриховая кривая на рис. 3.9,6). На частотах /у<С/в белый шум (по определению) преобладает, поэтому вместо (3.58) надо записать уже известное нам выражение (3.56);
И тогда отношение сигнала (3.58) к шуму (3.61) будет равно
Как видно из этой формулы, величина Мс/Ш растет с ростом полосы. Но это справедливо до значений /у^/в; на частотах /у>/в преобладает ВЧ-шум, а формулы (3.58) — (3.60) нам уже доказали, что с ростом полосы ВЧ-шум растет быстрее сигнала. Таким образом, оптимальна полоса /у=/в. Строго говоря, используемый нами оптимальный фильтр с прямоугольной частотой характеристикой справедлив для ВЧ-шума, бесконечно быстро возрастающего выше частоты /в. Для ВЧ-шума вида Р//в2 согласно (3.46) частотная характеристика несколько размывается в окрестности (штриховая кривая на рис. 3,9, в). Это размытие учтем в следующем разделе, а пока останемся в
171
Рамках простой методики расчета: считая частотную характеристику прямоугольной, подставим значение полосы ^й в
(3.62):
_ (3'63> „оф 5ВсАГ2У( 3£сДУ2Гс ГТГ
=~ШГ у2Тс/° - У2ЙГ У к • (3'64)
Итак, и в первом случае (белый шум), и во втором (ВЧ - шум) был выбран фильтр с одной и той же по форме—прямоугольной — частотной характеристикой, И в первом, и во втором случаях определяющей является белая компонента шума. Различие состоит лишь в настройке фильтра: в первом случае он настраивается по сигналу, его полоса fy=:^c = 1/2Гс> а во втором —по спектру шума, его полоса (и, стало быть,
Его не надо перестраивать при изменении длительности Тс), Поэтому в обоих случаях для отношения Ыс/Ш справедливо общее выражение (3.62). При подстановке в него конкретного значения полосы настройки fy переходим к (3.57) в случае белого шума и к (3.63)—в случае высокочастотного. Однако эти формулы существенно различаются — вот к чему приводит различие лишь в настройке фильтра. Во-первых, сужение полосы от значения /с до значения ПрИводит к снижению отношения №с/щоф соответственно в У! с/!в раз. Во-вторых, узкая полоса (/у</с) привела к изменению самого характера зависимости Л^с/шоф от длительности Тс: она стала линейной, а не корневой. С точки зрения частотного анализа это объясняется линейным возрастанием спектральной плотности сигнала с ростом его длительности, Е0 (/) — ЕсА2Тс, поэтому при постоянной полосе /в линейно возрастает и выходная амплитуда (3.58). С точки зрения временного анализа при узкополосном фильтре (/у^/с) сигнал можно рассматривать как дельта-импульс, поэтому амплитуда на выходе всегда пропорциональна мощности (площади) входного импульса ЕсАТс (§ 3.5).
Низкочастотный шум типа Ц. Этот случай иллюстрируется рис. ЗЛО. Здесь частотная характеристика фильтра в принципе не может быть прямоугольной: напряжение шума на выходе такого фильтра теоретически будет бесконечным из-за бесконечной мощности шума l/f на низких частотах при $—>-0. Поэтому придется отказаться от «прямоугольного мышления» и перейти к «треугольному мышлению»: именно треугольной оказывается частотная характеристика оптимального фильтра согласно (3.45):
Ки) = ка'к{/), Ко' = Ка/с1/„ к (/) = //Д. (3.65)
Здесь нормировка коэффи - е,
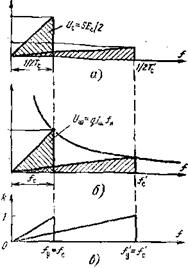 Циента передачи ли) про - „ 2Т ведена к его максимальному значению — значению 5Е^Ч на частоте / = ?с Возрастание плотности шума при снижении частоты (до бес - -2 конечно малых значении) привело к необходимости понижать на этих частотах / н усиление (до бесконечно?“/с малых значений). Методика расчета сигнала и шума не сильно усложнилась: их.
Циента передачи ли) про - „ 2Т ведена к его максимальному значению — значению 5Е^Ч на частоте / = ?с Возрастание плотности шума при снижении частоты (до бес - -2 конечно малых значении) привело к необходимости понижать на этих частотах / н усиление (до бесконечно?“/с малых значений). Методика расчета сигнала и шума не сильно усложнилась: их.
Опять можно рассчитать
Рис. 3.10. К расчету сигнала и дисперсии шума в случае НЧ - шума:
А —спектр сигнала; б— спектр шума; в — частотная характеристика фильтра
Как площадь под кривыми &(/)ес(/) и ^2(/)в(/), только теперь эти площадки треугольные, а не прямоугольные, как было
Имеем
£/с А - 5£'сл27'с $ / = ЗЕ^Г, $-£<*/ =
|
ЗЕС |
![]()
|
(3.66) |
![]() = 8ЕсА2Т±
= 8ЕсА2Т±
1 с с
£/ш = 2#/,Д К-Ьг1/ ■■■= 2?/ш ^
|
' с 2^1 |
|
/н /2 /са 2 |
|
|
|
|
Ни амплитуда, ни шум на выходе рассматриваемого фильтра не зависят от длительности входного сигнала. Из рис. 3.10, а наглядно видно, почему так получается для амплитуды выходного сигнала: площадь к([)ес([), которая определяет эту амплитуду выходного сигнала, всегда — при любой длительности Тс — уменьшается в два раза из-за треугольного характера ^(0- Можно сказать иначе: поскольку в рабочей полосе частот Усиление равномерно меняется в пределах 0...1, то среднее Усиление равно 0,5, поэтому амплитуда и уменьшилась вдвое. •Независимость выходного напряжения шума от вариации дли-
Тельности ВХОДНОГО импульса иллюстрируется рис. 3.10,6. При коротком импульсе ТУ полоса фильтра конечно, расши
Ряется, однако пропорционально падает спектральная плотность шума на верхней частоте, © (/с) =/и//с', так что площадь под кривой, определяющая выходной шум, остается постоянной. Для большей наглядности на рис. ЗЛО рассмотрены дВа импульса с разными длительностями: площади Л(/)ес(/) и
£2(/)0(/) для них остаются неизменными. Поскольку сигнал и шум не зависят от длительности Тс, то и их отношение инвариантно по отношению к этому параметру:
Д^оф _ ^с. А __ 1 гс 7ГС7 ^сА_ (9) ^
С/Ш иш " 2 У?/Ш/н ’ У2^/ш/„ ■ * ’ *
Отношение точный расчет, учет влияния формы
Сигнала. Пока нами рассматривался простейший (прямоугольный) спектр сигнала, который был выбран ради наглядности и простоты анализа. Но, строго говоря, прямоугольный спектр является спектром сигнала вполне определенной формы —колоколообразной с периодически затухающими фронтами вида
Бшх}х, х=^]Тс (рис. 2.1,#, см. §2.1). Правда, в том же
§2.1 было показано, что спектр любого колоколообразного сигнала аппроксимируется прямоугольным спектром, так что можно ожидать, что все полученные выражения для отношения А^ш имеют достаточно общий характер. Но все-таки, как изменится отношение А’слд, если провести его строгий расчет
С учетом возможной вариаци'и спектра ес(/)? Как сильно будет влиять форма сигнала (вариация спектра £с(/)) на значение Для ответа на эти вопросы проведем точные вычисления величины А^сдц последовательно для тех же трех случаев, когда вреобладает белая, ВЧ - либо НЧ-компонента шума.
Белый шум. Преобразуем общую формулу для отношения сигнал-шум (3.49) к следующему виду:
/уЦ5 _ О'л 1 / Г ес"(/) . * ^£СА п 6°)
*с1щ-~тт Тс у б! ь ( ’
^Г~____________ . / (“ еС£(/И/
2г=5 Ш‘V - Ут~ V =—• (з-70)
0 Г Гвс(/)йГ/
О
В последнем выражении учтен характер белого шума,
В(/) — 1 и введена эффективная полоса сигнала /с— 1 /27*с;
Согласно определению (2.15) она заменена интегралом — площадью под кривой ес ([). Как видим, отношение отличается от полученного выше (3.57) только численным коэффициентом V-
Этот коэффициент равен корню квадратному из отношения двух полос: шумовой полосы оптимального фильтра к эффективной полосе сигнала /с. Или, учитывая определение полос /ш $с, коэффициент равен корню из отношения площадей под
Кривыми ес2(Нт ес(/)‘
Однако значения этих площадей различаются весьма незначительно. Действительно, при рассмотренном выше прямоугольном спектре ес2(П = (/) = I И рассматриваемые площади рав
Ны ДРУГ ДРУГУ' так что Т“!« В общем случае площадь под кривой ес2(/)> конечно, меньше, поскольку е(/)<С1 (во всяком случае, это справедливо при ес(/)>0). Однако для рассматриваемого класса импульсов спектральная плотность (/) уменьшается достаточно быстро в окрестности частоты! С=1/2ТС. Поэтому площадь под кривыми ес2(?),ес(!) определяется в значительной мере площадью в области плато, где опять-таки ес2(!) &ес(1)«I; ширина этого плато порядка 1/2 Гс. Так, далее качественное рассмотрение выражений (3.69), (3.70) позволяет сделать еще один важный вывод: для рассматриваемого класса колоколообразных импульсов и коэффициент у, и, следовательно, отношение Агс/шоф достаточно слабо зависят от относительной формы сигнала (при постоянной эффективной длительности), Подтвердим этот вывод расчетами для импульсов прямоугольной и косинусквадратной формы.
Прямоугольный импульс:
|
/ |
СО Г со
|
V |
![]() 2ГС^(/)<*/ = У 2Л е1(Тс/) =
2ГС^(/)<*/ = У 2Л е1(Тс/) =
2 (* эт2 х, * '
-г—
Я 3 хл
О
Косинусквадратный импульс:
|
/ |
Оо /~оо
О-г Л/ С Вш22д/Г^(/2Гс)
2ГС Ус </)<*/ у } (2л/Гсу. ({_4рТс*у
О о
__1 / 1 ? ып2хйх____________ А Г 3
V я ] х2(1 — х*(п2)2 V 4 '
ЛГ™ = У2ч = ГТ 1/4=
1 У2?/ш У ' 4 У2Я1Ш
1,22—-;1^'с-. (3.72)
|
V/ г, г |
![]()
|
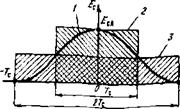
Рис. 3.11. Две аппроксимации колоколообразного импульса |
![]() Здесь использованы таблицы интегралов [79]. Получили даже неожиданный, слишком хороший результат: формула (3.71) для импульса прямоугольной формы в точности совпала с прежней формулой (3.57), рассчитанной для эффективного прямоуголь - спектра. Это выражение дает максимальное значение при
Здесь использованы таблицы интегралов [79]. Получили даже неожиданный, слишком хороший результат: формула (3.71) для импульса прямоугольной формы в точности совпала с прежней формулой (3.57), рассчитанной для эффективного прямоуголь - спектра. Это выражение дает максимальное значение при
Обнаружении импульсного сигнала.
При другой форме сигнала —при «размазывании» энергии импульса по времени, когда часть энергии из максимума переходит в «хвосты», как это имеет место в колоколообразном сигнале, отношение А:с/щ может только уменьшаться. Правда, для косинусквадратного импульса «размазывание» энергии незначительно» как незначительно и унижение Л^ш (всего на 13,5%, ср. (3.71) и (3.72)). Впрочем, такое снижение Л^ш можно было предсказать, пользуясь только формулой (3.57), полученной при качественном анализе в предыдущем разделе. Так, в соответствии с § 1.3 колоколообразный импульс
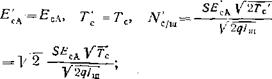 (рис. 3.11, кривая 1) заменяем эквивалентным ему прямоугольным импульсом той же амплитуды Е'сА=Еса и эффективной длительностью ТС' = ТС (рис. 3.11, кривая 2). Но ведь эквивалентную замену можно выполнить по-другому: сохранить длительность по основанию ТС” = 2ТС, тогда эффективная амплитуда (из условия равенства энергий) будет составлять ЕсА = = Есл12 (рис. 3.11, кривая 3). Для этих двух импульсов получим
(рис. 3.11, кривая 1) заменяем эквивалентным ему прямоугольным импульсом той же амплитуды Е'сА=Еса и эффективной длительностью ТС' = ТС (рис. 3.11, кривая 2). Но ведь эквивалентную замену можно выполнить по-другому: сохранить длительность по основанию ТС” = 2ТС, тогда эффективная амплитуда (из условия равенства энергий) будет составлять ЕсА = = Есл12 (рис. 3.11, кривая 3). Для этих двух импульсов получим
|
|
Реальный колоколообразный импульс лежит посередине этих крайних прямоугольных аппроксимацией, так что следует ожидать среднего значения.
Л* К/ш + __ I + УТ 5ЕсА У>С_, ^ 0£^СА_УТ7
------ 2--------- 2 у 2^- (3'75)
И опять получили очень хорошее (до третьего знака) совпадение с точной формулой (3.72).
Высокочастотный шум. Пусть ВЧ-шум преобладает во всей области спектра сигнала, /В<^1/2ТС. За счет сильного роста шума 0^ Р подынтегральная функция в формуле для отношения (3.49) резко падает в окрестности частот в. Эти частоты относительно спектра сигнала весьма низкие, здесь плотность спектра сигнала постоянна, ес(/)=1. Это условие облегчает вычисление интеграла:
СО оо со
СесЧО */ „ Г С *(///»)
.) 0(/) О0(/) ■/в.) 1+(///в)2
ООО
Для отношения сигнал-шум имеем і.
ЛГоф 5ёсА2Гс -./ РегіП
■ V }іпл =
= і/йІ^і//в = 2,5-№-^Л - (3.77)
У¥ш У 2яіш
■Как видим, форма сигнала в этом случае не влияет на значение №с%: ведь оптимальный фильтр пропускает только низкие частоты, где относительная спектральная плотность для сигналов любой формы одна и та же, ес=1. Те же частоты, где поведение спектра зависит от формы сигнала (в окрестности ї~ї= 1/2Гс и выше), вклада в интеграл (3.76) не дают (из-за большого значения знаменателя 0(/) ~/с2//в2^> 1).
Точное выражение (3.77) дает несколько большее значение чем приближенная формула (3.63). Объясняется это тем, ЧТО при приближенном расчете форма частотной характеристики фильтра выбиралась прямоугольной (непрерывная кривая на рис. 3.9,в). Оптимальный фильтр сглаживается и имеет быстро спадающий «хвост» на частотах (штриховая кри
Вая на рис. 3.9, в). Вклад гармоник этих частот и привел к некоторому возрастанию Л'с/щ в точной формуле (3.63),
Низкочастотный шум. Подставляя в (3.49) спектр щума в=7н//, получаем для импульса прямоугольной формы
|
|
|
|
На больших частотах (/>1/2Гс) подынтегральная функция падает очень медленно, 1//, поэтому интеграл от нее ( со1п^ на бесконечности расходится, N -*оо. Второй раз сталкиваемся со случаем, когда шумы вроде бы не ограничивают обнаружение. Однако это умозрительный случай — полученная формула справедлива при трех условиях (трех «бесконечностях»), которые на практике реализоваться не могут:
Усиление оптимального фильтра должно простираться до бесконечности
|
(3.79) |
![]() Эт я/Тс
Эт я/Тс
Л/т с (/н//)
А в реальных случаях полоса всегда ограничена:
С ростом частоты шум в нашей модели становится бесконечно малым, в^/н/^О, реально минимальная величина шума будет ограничена хотя бы белой составляющей (подобная ситуация встречалась для ВЧ-компоненты шума на частотах ^0);
Рассматриваемый прямоугольный импульс — это импульс с бесконечной скоростью нарастания фронтов; длительность реальных переходных процессов всегда конечна, поэтому спектр сигнала спадает с ростом быстрее, чем 1//, и интеграл в (3.78) сходится.
Чтобы избежать неприятности, связанной с расходимостью, достаточно учесть только последний фактор — конечную длительность фронтов. Так, для сигнала колоколообразной формы
|
Здесь введено обозначение х = 2л/Тс‘, значение интеграла найдено с помощью таблиц [79]. |
Точные вычисления отношения с учетом конкретной
Формы сигнала (прямоугольной, колоколообразной) полностью подтвердили прежние, приближенные формулы, лишь незначи
Тельно (в пределах-0... 20%) уточнены значения численных коэффициентов (особенности случая НЧ~шума и прямоугольного импульса только что были оговорены). Все полученные формулы для удобства сопоставления и использования сведены в табл. 3.2. Эти формулы имеют столь большое значение в теории
Таблица 3.2. Отношение сигнал-шум на выходе оптимального фильтра
Значение коэффициента а
|
1^2дIш/н „ *~*^сА У Т с. Ш Т $ЕсАТс |
|
Отношение сигнал-шум |
|
Приближенное (прямоугольный спектр сигнала) |
|
Точное |
|
Характер шума |
|
Дг°Ф С/щ |
|
Колоколо Обратный Импульс |
|
Прямоугольный мпульс |
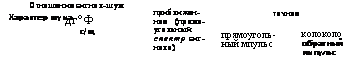 |
|
|
|
|
|
|
|
|
|
|
|
|
Обнаружения, что их анализу посвятим весь следующий параграф. А пока для общности нам осталось сделать еще один последний шаг — рассмотреть произвольный спектр шума, кот - рый может встретиться в ФПУ.
Отношение сигнал-шум при произвольном спектре шума. В общем случае в спектре шума ФПУ могут присутствовать все три компоненты 1 jft 0 = const, 0^/2 2.4). Чтобы об
Ласть белого шума не перекрывалась полностью НЧ - и ВЧ-шу. мами, должно выполняться условие f„<fB (рис. 3.12,а). Точные формулы для отношения Ncfui в случае такого спектра весьма громоздки и здесь не приводятся. Попытаемся найти удобные для практики аппроксимации. Воспользуемся тем, что при вариации полосы частот сигнала в зависимости от его длительности может стать преобладающей лишь одна из трех шумовых компонент: при узкополосном сигнале (сигнал большой длительности), когда fc = l/ST’cC/u, это НЧ-компонента, при средней полосе сигнала — белая и при широкополосном
Сигнале /с»/в — ВЧ-компонента (рис. 3,12,а, б). Поэтому отношение при указанных длительностях импульса Тс опи
Сывается полученными выше выражениями для таких частных случаев. Обратимся сначала к приближенным формулам (3.57),
(3.63) , (3.68) и перепишем их в унифицированной форме:
TOC o "1-5" h z f f У°ф SgcA У~2Ге________ I ("З
С/ш У2?/ш у277 " У 2^ V2fn(2Tc)' (' }
F < f С f №* SEсА ^2Тс 1 ■ П
С/ш ущ - уГ (3.82)
SEcATc г— SE к V 277 1
/в < /с, - 2 ]//в - - с* , . (3.83)
У УС ' V2 qlm У 1/С/в27’с) V '
Попытаемся сконструировать искомую аппроксимацию для отношения Nl%x при произвольной длительности Тс путем обобщения этих формул. Они отличаются последним сомножителем— сложим все три члена пэд корнем этих сомножителей:
F // f дгоф ___ УГ2У‘с I_____________________________ . д.
/н</В. с/ш - Ущ - /2/н(27'с)+1 + 1/(/в27’с) '
Это выражение можно представить еще в одном, удобном для запоминания виде, если провести замену 1/2Гс-^/с:
QP
/„«/„ N1%,=—*= -.А г - - (3.85)
VWv>lU + 2fn + (.U/f,)fc]
Такая форма записи настолько наглядна, что вряд ли требует комментария: отношение сигнал-шум и есть отношение амплитуды сигнала SEca к шуму, рассчитанному в некоторой эквивалентной полосе. При белом шуме эта полоса равна полосе сигнала fc Вклад избыточных шумов формально учитывается воз - пястанием эквивалентной полосы: для НЧ-компоненты на величину 2[н и для ВЧ-компоненты на величину |с2/[„.
Как "было показано выше, при точном расчете для
Колоколообразного сигнала несколько уточняются значения численных коэффициентов, поэтому и в обобщенной формуле (3.85) численные коэффициенты следует уточнить. Пользуясь прежней методикой, получаем
= 0'865^7^^" ^ 2-1/и(27-с) ; (3'86>
/.</«</.. л'&=' (з-87)
—; (а88)
Согласно этим выражениям уточненная аппроксимация должна принять следующий вид:
^ 0,8655£сА УТ!
/-</»• —х л
У 1 (3.89)
У2Л/«(2Гс)+1+0.48//,-2Гс
При вариации длительности сигнала Тс одно из трех слагаемых под знаком корня может становиться преобладающим, и тогда общее выражение (3.89) совпадает с соответствующим асимптотическим выражением (3.86), (3.87) либо (3.88). Остается нерешенным только один вопрос: будет ли справедли
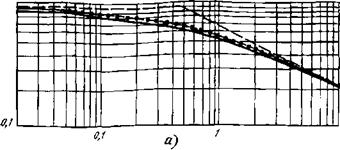
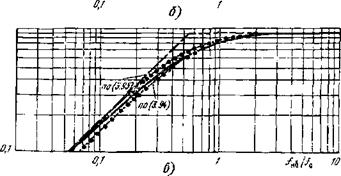
Вым найденное выражение и в переходных областях, когда /с~/н или /сЯ^/в? Ответить на этот вопрос можно сравнением аппроксимации (3.86) с точным значением А'с/’ш, рассчитанным по (3.49). Такое сопоставление и приведено на рис. 3.13. И здесь нам сопутствует успех: простая аппроксимация (3.89) оказалась достаточно точной не только там, где нам это заранее было известно (в области асимптот), но и в переходных областях, окрестностях характеристических значений Iс = /н и /с = /в. Погрешности здесь составляют всего 7... 9%. Мы вправе говорить «всего», потому что точности измерения параметров сигнала и шума ФПУ обычно не лучше, так что такая точность расчета, как правило, достаточна. Если все-таки нужен более точный расчет, то на переходных участках следует пользоваться кривыми рис. 3.13.
|
/ ОШН- 1
|
|
Муш. , О/!}//. Л? 1
|
|
|
|
0,1 |
|
М1^ш» |
|
<М7Ж Л? |
|
/ |
|
4А л? |
|
Рис. 3.13. Зависимость отношения N от длительности сигнала (его полосы /с—1/2 Тс) при различном спектре шума ФПУ: ШумЛь.|; 6— белый и ВЧ-шумы; е — НЧ-и - ВЧ-шумы. Нормировка проведена к значению Л при преобладающей белой {а, б) либо низкочастотной ___________ (е) составляющей шума: Точная зависимость; . . , приближенная зависимость;---------------------- асимптота |
В заключение рассмотрим случай «перекрытия» НЧ - и ВЧ-компонент шума. Хотя вероятность такой ситуации в реальных ФПУ мала, однако ради общности анализа рассмотрим и эту ситуацию (рис. 3.12, в). Область белого шума исчезает, появляется новая характеристическая частота на которой мощности компонент низкочастотного (0 = /н//) и высокочастотного (0 = ^ //в2) шумов сравниваются:
/ = /нв, /н//нв=/нв2//в2, /нв3 = /н/в2. (3.90)
При длинном импульсе преобладает НЧ-компонента и все проведенные выкладки (3.86) остаются справедливыми. Однако при коротком импульсе, когда /нв<С/е:= 1/2ТС} расчет сигнала и шума надо уточнить. Как мы знаем, полосу оптимального фильтра следует ограничить характеристической частотой с которой начинает резко расти ВЧ-шум, — в данном случае’частотой /нв. в выбранной полосе фильтра О — /нв доминирует НЧ-составляющая, частотная характеристика фильтра треугольная, напряжение выходного шума в таком случае не зависит от полосы и задается формулой (3.67), а сигнал рассчитывается по аналогии с (3.66) следующим образом:
УсА=(5£сА27,с)(Ы2). (3.91)
Тогда для отношения сигнал-шум
ЖтО* ^сА 5£сА7’с/нв 0 ££сАГс -I /~ /нв Г (п поч
Сопоставляя эту формулу с полученной выше для ВЧ-состав- ляющей (3.83), видим, что эти формулы совпадут при следующей замене:
Обобщенное выражение (3.89) при такой замене трансформируется следующим образом:
/Ч»/- ЛГ«* 0,8655£(А/2Т;
48 2/н
Уг2д1ш~^/ 2,1/н (2ТС) + (2ТС) 0.65ЕсА
- т------------------------------ ------------------------------------------- (3.94)
У2<?/ш/а V 1+0,46/(Гт2Гсу
Методом подгонки удается уточнить коэффициент в этой аппроксимации:
Г - Г Л70ф _ 0>6^£сА_____________________ !___________________ /я
Ун >/в. С/Ш У2^ГН Уі+0,307І(/„в2ТсГ
Эта аппроксимация, как и предыдущие, с достаточно высокой точностью (не хуже 12%) совпадает с численным расчетом Ірис. 3.13).
Подведем итог. Фактически итог этому параграфу уже подведен в "табл. 3.2. К этим формулам следует добавить и (3.89), (3.95). Во всех практически важных случаях отношение сигнал-шум на выходе оптимального фильтра Л^щ удается рассчитать с помощью этих достаточно простых формул, если известны параметры сигнала Тс, чувствительность ФП 5
И характеристики шума /ш, /ы, /в. Мелкие детали формы сигнала слабо влияют на это отношение. Характер шума изменяет зависимость от
Длительности сигнала: при ВЧ-шуме она линейна (Л^?ш ог Тс)> при белой становится корневой (Л^ш <N3 У^Г^ а ПРИ избыточном шуме зависимость ^сдц от длительности сигнала вообще исчезает.