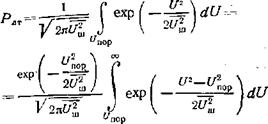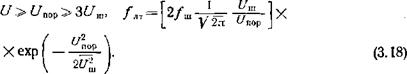Фотоприемные устройства и ПЗС. Обнаружение слабых оптических сигналов
Основы теории оптимальной фильтрации в приложении к фотоприемным устройствам ПРИНЯТИЕ РЕШЕНИЯ О НАЛИЧИИ ИЛИ ОТСУТСТВИИ СИГНАЛА
Предыдущим параграфом завершается анализ прохождения сигнала через линейный тракт ФПУ, рассмотрение шумов этого тракта. Были приведены формулы для расчета напряжения на выходе усилителя — напряжения шума либо шума в смеси с сигналом (если сигнал приходит на вход ФПУ).
Зная напряжение на выходе каждого канала, можно теперь перейти к задаче собственно обнаружения, ответить на основной вопрос, ради которого и создается ФПУ: пришел оптический сигнал на его вход или нет? Рассмотрим круг вопросов, связанных с этим решением: с помощью какого правила принимается такое решение? Насколько оно будет достоверно?
Принятие решения о наличии или отсутствии сигнала. В оптико-электронных системах допустимы только два конкрет-* ных решения: «сигнал есть» и «сигнала нет». И возможны только две ситуации — сигнал пришел либо не пришел на вход ФПУ. В каждой из этой ситуации система может принять любое из указанных решений — «сигнал есть» либо «сигнала нет», так что возникают четыре комбинации.
1. Сигнал не пришел. Решение — «сигнала нет». Принято Правильное решение об отсутствии сигнала.
2. Сигнал не пришел. Решение — «сигнал есть». Это ошибочное решение называют ложной тревогой (ошибка первого рода).
3. Сигнал пришел. Решение — «сигнала нет». Это — ошибка второго рода или пропуск сигнала (цели).
4. Сигнал пришел. Решение — «сигнал есть». Принято правильное решение о наличии сигнала.
В качестве количественной характеристики вводят вероят
ности указанных ошибок — вероятность ложной тревоги Рлт (вероятность принятия решения «сигнал есть», если априори известно, что сигнала нет) и вероятность пропуска Рир (вероятность принятия решения «сигнала нет», если априори известно, что сигнал есть) [4, 75]. Тогда вероятности принятия правильных решений об отсутствии сигнала или его наличии соответственно равны (1—РЛт) и (1—Япр). Введенные величины Рлт и Рдр являются важнейшими характеристиками системы обнаружения: чем меньше значения Рлт, Рщ,, тем качественнее система, достовернее ее решения.
Правило принятия решения. В качестве решающего в системах обнаружения применяется пороговое устройство (дискриминатор). Смесь сигнала с шумом данного канала подают на вход этого устройства. Пусть момент прихода оптического импульса на ФПУ априори известен, тогда известен и момент tu—момент достижения сигналом на выходе усилителя (на входе решающего устройства) своего максимального значения. В этот выгодный момент и принимается решение о наличии или отсутствии сигнала. Алгоритм работы дискриминатора весьма простой: если поданное на него напряжение U{tu) превышает некоторый заданный пороговый уровень (порог срабатывания) f/nop, принимается решение «сигнал есть», если U(t№) ниже порога Unoр, принимается решение «сигнала нет»:
U(tK) <.UU0V, решение—«сигнала нет», *
(ЗЛ)
U (^м)^^пор, решение — «сигнал есть».
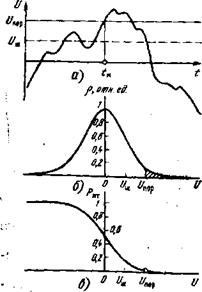 Вероятность ложной тревоги. Согласно определению вероятность РЛт рассчитывается, когда сигнал отсутствует и на вход дискриминатора подается реализация шума (рис. 3.1,а). Причиной ложного срабатывания в этом случае становится шумовой импульс, если в момент принятия решения /м шум £/(/*) превышает значение порога срабатывания С/пор. Вероятность этого события легко подсчитать. Вероятность того, что в момент U напряжение шума лежит в
Вероятность ложной тревоги. Согласно определению вероятность РЛт рассчитывается, когда сигнал отсутствует и на вход дискриминатора подается реализация шума (рис. 3.1,а). Причиной ложного срабатывания в этом случае становится шумовой импульс, если в момент принятия решения /м шум £/(/*) превышает значение порога срабатывания С/пор. Вероятность этого события легко подсчитать. Вероятность того, что в момент U напряжение шума лежит в
Рис. 3.1. Ложная тревога при большом положительном выбросе шума (а) и расчет вероятности ложной тревоги (б—в)
Пределах и.-'У^г^и, обозначим р(£/)*Ш; она задается нор* мальным законом (2.65) (рис. 3.1,6); в нашем
Случае о2= £/ш2,
Иа=У От2 (возможные в ФПУ отступления от нормального закона рассматриваются в § 4.3, 4.4). Поскольку при всех значениях и^Оио? принимается решение о наличии сигнала, то надо найти вероятность того, что и лежит в области [£/ПОр...
Оо], т. е. проинтегрировать в соответствующих пределах функцию р(Ш:
ОО ОО
Ипор г/— ш /
ОО
|
, и V2 U, |
![]() -П ] ехр[-ЫУ!
-П ] ехр[-ЫУ!
'пор
^пор^2
Решение этого интеграла находится с помощью функции ошибок Ф(г):
ОО ^ПОр IУ2
-J$exp(—x2)dx— у== j ехр(—x?)dx
= М 1-ф(ж)]; " (3-2б)
Z
Ф(2) = ? ехр ( — X2) (&С, 4Цоо)'=S I.
^ о •• ■
Функция ошибок является одной из самых известных специальных функций, часто встречающихся в статистике, анализе явлений диффузии и других разделах физики. Ее таблицы приведены, например, в [76].
Зависимость вероятности ложной тревоги от порога срабатывания иллюстрируется рис. 3.1, в и табл. 3.1. Здесь проявляется удивительное свойство нормального закона: вероятность появления малых значений U — не более (1...2) Um — велика и относительно слабо падает с ростом U, зато большие значения U>3Um маловероятны, зависимость р(£/) при таких
|
Таблица 3.1. Вероятность ложной тревоги резко падает с увеличением порогового напряжения
|
Больших напряжениях шума становится черзвычайно резкой— спадает с ростом V сильнее экспоненты. Иными словами, реализация 6фм) как бы «сконцентрирована» в узком
1/~—2*
Диапазоне значений порядка ±2 V С/ш> шумовые выбросы за пределы этого диапазона чрезвычайно редки. Заметим, что на этом свойстве нормального закона основана известная приближенная методика оценки среднеквадратичного значения шума
УЖ по осциллографу: на экране прочерчивается ряд реализаций с вероятными выбросами в пределах + (2...3) и наблюдается шумовая дорожка шириной (двойным размахом)
И^4...бУ £/щ. По ширине дорожки рассчитывается шум,
V Ьт2т /(4 ... 6). В этом контексте напряжение шума
У иш не просто статистическая характеристика (среднеквадратичное значение). В это понятие как бы вкладывается прямое содержание термина. Действительно, для детерминирован - ной гармоники ее среднеквадратичное (во времени) значение
У и2т характеризует пределы, в которых эта величина колеблется (в пределах ± У 2£/щ ). Для случайной величины (нормального шума) получили полную аналогию с детерминированной: вероятные значения шума сосредоточены почти в тех
Же пределах порядка ±2У и2т.
Указанная особенность нормального закона — слабая зависимость р(и) при малых значениях V и сильное падение р(^) при больших II — еще более подчеркивается в функции ошибок и, следовательно, в приведенной зависимости РЛт(£Агор)* При пороге ипор—0 вероятность Рлт = 0,5, так как положительные и отрицательные выбросы шума равновероятны. При изменении иао1)/иш от 0 до 1 вероятность Рлт падает относительно мало, от 0,5 до 0,159. Но уже при порогах срабатывания £Аюр= (2 ... 3) ит вероятность РЛТ становится достаточно малой, 2(10-2,.. 10_3), и очень резко спадает с ростом повыше
Ние и по р/^ш всего на единицу приводит здесь к уменьшению
р примерно на два порядка. Это легко показать с помощью ппиб тижения для вероятности Рлт, справедливого При больших значениях порога срабатывания. Перепишем (3.2, а) в виде
Преобразуем показатель подынтегральной экакдаенты:
TOC o "1-5" h z Ц'-иІр (^-^п. р)^+^ор) ' .; '
2и‘ш 2 С/‘
А и (2 ипор + Ш)
^пор
2£^ и1
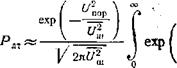
|
= Д£/|(/Д£/ = |
![]()
|
Ехр |
![]()
|
Пор |
![]()
|
Л. |
![]()
|
И1 |
![]() Здесь введено приращение над порогом АС/ и учтено, что в рассматриваемом случае больших порогов (£/Пор>3£/ш) экспонента падает быстро в пределах малых приращений А(/<(/ПОрт поэтому (3.3) принимает вид
Здесь введено приращение над порогом АС/ и учтено, что в рассматриваемом случае больших порогов (£/Пор>3£/ш) экспонента падает быстро в пределах малых приращений А(/<(/ПОрт поэтому (3.3) принимает вид
* ^ехр(-^). (3.5)
Раскладывая в ряд функцию ошибок в (3.2,6), также придем к последнему выражению (3.5). Полученное приближение очень удобно для практических расчетов Рлт(^шр)- Так, из этой формулы следует, что благодаря сильной зависимости РЛт °т порога срабатывания (практически по нормальному закону) этот самый порог может выбираться в относительно узком интервале ипор= (3 *.. 6) иш. При столь малом изменении порога {всего в два раза) вероятность ложной тревоги уменьшается
|
Ехр |
![]()
|
Пор |
![]()
|
И пор 20^ |
![]()
|
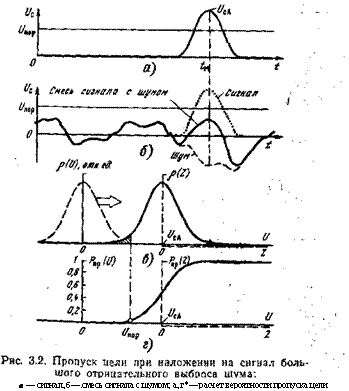
А — сигнал, б—.смесь сигнала с шумом; а, г*— расчет вероятности пропуска цели |
|
*1,5-10-8... 1СИ. (3.6) Вероятность пропуска цели. Пусть теперь на ФПУ подается оптический сигнал. Соответствующий ему сигнал на выходе усилителя ису) изображен на рис. 3.2, а. В момент /м амплитуда выходного сигнала £/са“£ММ превышает порог, ^сл>^пор, решающее устройство принимает решение «сигнал есть». Однако в момент /м может быть значительным отрицательный шумовой выброс — столь значительным, что общее напряжение смеси сигнала с шумом окажется меньше £/ПОр. Ре- |
 Чрезвычайно резко (на шесть порядков) и перекрывает весь диапазон значений этого параметра, требуемый обычно в оптико-электронных системах*.
Чрезвычайно резко (на шесть порядков) и перекрывает весь диапазон значений этого параметра, требуемый обычно в оптико-электронных системах*.
Шающее устройство примет ошибочное решение «сигнала нет* (пропуск дели), рис. 3.2, б.
Вероятность пропуска цели рассчитывается по аналогии с предыдущим случаем. Поскольку априори известно, что в момент tu сигнал равен амплитудному значению UcA, то вероятность получить суммарное напряжение смесн сигнала с шумом и=*иса+£Лп(*м) равна вероятности получить шум £/ш(*м) = = [U—С/са)’
Р (С/) cff/——=~"бхр [ (£/ Ј/cAp/2Ј/inJ. (3.7^
При всех значениях С/ < £/пор решающее устройство ошибется — пропустит цель, так что
|
Г/, |
|
Илор = J р (£/) rft/ |
|
Пор |
|
Exp - |
|
_•], у &сл-U)' 2игш |
|
Лр |
|
2nUl |
|
U^-u |
 |
|||
|
|||
|
|||
|
|
Как видим, при расчете РЛт и Рпр приходим к идентичным интегралам, отличающимся только нижним пределом (ср. с ■(3.2а)). Поэтому формула для РПр следует из формулы для - Рдт простой заменой иПОр-^иса—Упор:
-®(Uch-Un0Sl)lV2U,
Естественно, при больших аргументах остается справедливой аппроксимация (3.5), если, конечно, провести ту же замену Утр-ь-УсА—Опоу'
|
^сА ^пор |
|
>3, Р |
|
Пр |
|
£Л |
|
X |
|
У"2л (^сА—^пор) |
|
(3.9> |
![]()
|
Хехр |
![]() (^сА—^пор)'
(^сА—^пор)'
2Ul
Зависимости р(У), Рдр (Упор) приведены на рис. 3.2,в, г. При сравнении их с рис. 3.1 (а также при сравнении формул (3.8), ,(3.9) и (3.2), (3.5)) видна очевидная аналогия функций Рлт(ипор), Рпр(1/»ор). кривые р(С/) сдвинуты относительно Друг Друга на величину амплитуды С/са- максимум первой из них ДОСТИГаеТСЯ ПрН итаУ< = 0 (СМ. рИС. 3.1), а ВТОРОЙ — При С/тах =
= £/сА (рис. 3.2). Вероятности Рлт> ^пр представляют площадь под кривой р(£/), точнее, площадь «хворта» этой кривой д0 значеняи ипор:
![]()
|
Шзх |
![]() (3.10)
(3.10)
Функции Рдт, Рпр можно рассматривать как интегральную вероятность для всех значений [£Люр, °о] и [—оо, С/аоР] соответственно. Из (ЗЛО) следует, что все сказанное о характере поведения Рдтфвоъ) ■ остается справедливым и для функции
Рпр ( ^пор) .
Отношение сигнал-шум как основной критерий качества системы наблюдения. Перенесем на рис. 3.3,а, б обе кривые Ячт(и), РПр{и). Из рисунка видно, что для уменьшения вероятности Рлт порог £Люр должен как можно дальше отстоять ог шума £/ш, а для уменьшения вероятности Рпр — сигнал £/сА от порога ипор. Отсюда следует одно из важнейших положений теории обнаружения:
Основной характеристикой качества обнаружителя является отношение сигнал-шум (на входе решающего устройства), Л^/ш = Уса/^ш.
Комментарии здесь излишни. Каждому разработчику обнаружителей сигналов (и не только оптических) известно, что отношение сигнал-шум надо увеличивать. Само собой кажется понятным, что чем больше превышение сигнала над помехой, которая мешает его зарегистрировать, тем надежнее обнару-
Жится сигнал. Отношение Ыс/ш уже использовалось, , когда рассматривалось внутреннее усиление ФП (§ 1.2). Здесь отношение Л^с/ш как критерий
Качества получено не из об
Щих соображений: с помощью формул (3.2), (3.8) его значение однозначно связывается с вероятностями ложной тревоги и пропуска целй.
Выбор порога срабатывания. Требуемые значения отношения сигнал-шум. Как было показано, порог срабатывания выбирается обычно в пределах £/поР=(3...6 )£/ш (3.6). Те-
Перь к ЭТОМУ можно добавить, что положение £/пор на отрезке [t/ш, ^са] уточняется в зависимости от того, какая ошибка нежелательней: если опаснее ложная тревога, то значение Unop выбирают дальше от значения шума (Ли, а если пропуск цели, то ближе к нему (дальше от сигнала). В ряде случаев цена ошибок одинакова — равно нежелательны как ложные срабатывания, так и пропуск цели. Это относится, например, к ВО СП, где нельзя принимать логический нуль за логическую единицу (ложное срабатывание) и, наоборот, логическую единицу за логический нуль (пропуск сигнала). в этом случае минимизируют суммарную вероятность ошибки (3.2), (3.8)
{10, 38]:
О--»,+л.->-тИ$0+«(£7тоН - |зп|
Суммарная ошибка как функция порога срабатывания представлена на рис. 3.3, г. Из рисунка видно, что минимум ошибки достигается при таком пороге Uaopopt, когда вероятности ложной тревоги и пропуска цели равны: при L/nop> С/ИОр opt вероятность Рпр возрастает круче, чем падает вероятность Рлт, а при /Лшр<£Лор opt возрастание Рлт преобладает над снижением РПр. Из (3.2), (3.8) следует, что вероятности Рлт, Рар сравниваются, когда порог равен половине амплитуды выходного сигнала:
U„„p/V2l/ ш=(f/сл - £/„«*)/V2Ua, Um „ = U *12.
Таким образом
^пор 0pt= Uca/2, min Рош=2Рпр(^пор opt) =2Рдт (^пор opt)
= —<S>{UcjJ2i2Um). (3.13)
К этим же формулам мы придем, если приравняем нулю производную ошибки (3.11).
В ВОСП недопустимы искажения передаваемой информации, требования к вероятностям ошибок особенно жесткие,
Дш=10~9, рЛТ = рпр=5> Ю-10 [10, 38]. при этом согласно (3.2), (3.12)
Опор = 6,Шш, исА = 2 и Пор = 12,2 иш. (3.14)
Для других оптико-электронных систем требования К Рот, ^лт, Рпр обычно менее жесткие. С учетом сказанного имеем
^nopДJ (3...6) £Ли, UcA «2С/аоР=;(6...12)£/ш. (3.15)
Эти значения порога срабатывания и требуемого отношения сигнал-шум можно считать типовыми для оптико-электронных
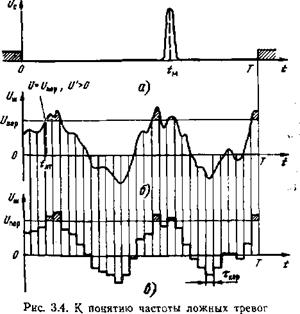
Частота ложных тревог. До сих пор рассматривался случай когда момент прихода импульса известен, так что известен и момент достижения им своего максимального значения на выходе усилителя, поэтому решающее устройство могло ВКЛЮЧИТЬСЯ именно в этот момент. Однако далеко не всегда момент прихода известен. Известен лишь некоторый достаточно широкий интервал времени — интервал наблюдения Т, импульс может прийти в любой момент этого интервала (рис. 3.4,а). Тогда решающее пороговое устройство включают на все время Т. При расчете вероятности пропуска цели все предыдущие рассуждения остаются в силе: причиной пропуска является все тот же возможный отрицательный шумовой выброс в момент *м» когда выходной сигнал достигает максимального значения; вероятность получить этот шумовой выброс амплитуды I У1 > I Уса—Упор) и определяет вероятность Япр.
Однако ложную тревогу теперь может вызвать не только шумовой импульс в момент ^м» но и любой такой импульс на интервале 7 На рис. 3.4, б приведена реализация с четырьмя шумовыми импульсами, вызывающими ложную тревогу. Надо подсчитать число всех таких импульсов Ылт. Поскольку это число зависит от интервала наблюдения, то вводится относительная характеристика — частота ложных тревог:
Глт = ЛГлт/7 (3.16)
Частота ложных тревог, определяющая число шумовых импульсов в единицу времени, и является характеристикой обнару-
|
|
Жителя в этом случае (конечно, имеются В ВИДУ Апттктпи* пульсы амплитудой и>ипор).
В § 2.2 специально столь подробно был рассмотрен шумо вой процесс и было показано, что качественно шумовая ПРЯ!! .зация может аппроксимироваться последовательное^ сов (рис. 3.4.в). Длительность этих шумовых импульсов равна времени корреляции тКОр. Время корреляции ткоо олое* АеЛЯЛОСЬ ВЫШе КаК Эффективная ДЛИтеЛЬНОСТЬ ФУНКНиГ*пппГ ляции К(М)- Спектр функции КШ), как б^ло показано есть спектральная плотность шума. Если известна зффекти™*« полоса этого спектра (назовем ее шумовой полосой М ™ известно и время корреляции, и эффективная длительноЛь мового импульса тш = тК0Р = 1/2/ш (такая связь длительности" ямпульса в данном случае функции К(М) - с его спектром была доказана в § 2.1). ^им
Аппроксимация реализации шума импульсной последовательностью (рис. 3.3,8) поможет рассчитать частоту ложной тревоги. Как видно из рисунка, общее число шумовых выбво - СОВ В единицу Времени
FлT Общ 1 /Тщ 4 2^^ |
?ДбааКт0ывТания°г7аСТЬа И3 "НХ пРев0СЗ[°Дит ™ амплитуде порог
Сраоатывания ипор; эта часть уже была рассчитана (3 5)
Оц°Энку‘У ДЛЯ частоты ложных тревог получим следующую
|
Множитель в прямоугольных скобках назовем характеристической частотой: |
|
При численной оценке для отношения порога срабатывания к |
Д "I------------ '
Шуму приняты ее типовые значения согласно (3.15). Формула (3.18) переписывается следующим образом:
|
(3.20) |
![]() У ят— /хар 6Хр ( ■ ипор12иш]'
У ят— /хар 6Хр ( ■ ипор12иш]'
![]()
|
(3.21) |
![]() Вероятность ложной тревоги за весь выбранный интервал непрерывного наблюдения Т согласно (3.16) равна
Вероятность ложной тревоги за весь выбранный интервал непрерывного наблюдения Т согласно (3.16) равна
Здесь для /лт использовано выражение (3.18), в котором проведена замена 2/ш-*1/тш. Сопоставим теперь (3.21) с вероят - ностью ложной тревоги (3.5), когда момент прихода сигнала был известен и поэтому достаточно было взять одну выборку Шум сохраняет свое значение в течение тш = тКор, так что За все время Т, пока включено пороговое устройство, берем ТЫ кор разных отсчетов шума. Вот поэтому в Т'/ткор раз и увеличилась вероятность (число) ложных тревог (ср. (3.5) и (3-21)).
Для точного расчета /л г в статистической радиотехнике используют двумерное распределение вероятности для двух случайных величин—значения шума иш и его производной С/ш Ложную Тревогу в момент получают, когда С/Ш(*м)
И ^щ'(/лт)>0 (рис. 3.4,6). Такая методика приводит к выражению [52]
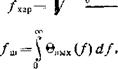
|
О |
![]()
|
Оо |
![]()
|
/’©вы |
![]()
|
/ш |
![]() /.т;' ~ /хзр ехр ( У пор/2£/ ш),
/.т;' ~ /хзр ехр ( У пор/2£/ ш),
(3.22>
Где ©вых(/) —относительный спектр шума на выходе. При белом входном спектре (0=1) спектр шума на выходе 0вых определяется частотной характеристикой усилителя, что вытекает из (2.42) — (2.44). Рассчитаем частоту /*ар для простейшего случая — усилителя с прямоугольной полосой пропускания:
|
О |
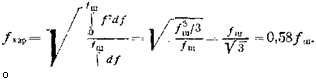 /</>-> *</)=!; />/г *(/)=0; /у=/ш;
/</>-> *</)=!; />/г *(/)=0; /у=/ш;
В § 4.1 будем рассматривать частотные характеристики реальных усилителей ФПУ, формируемых /?С-звеньями. Характеристическая частота ложных тревог таких усилителей /хар~/ш = = ±30%.
Сопоставление полученных выражений — приближенного (3.19), (3.20) и точного (3.22) —показывает, что они совпадают в рассмотренных примерах с точностью до множителя:
0, 58/(0,13 . .. 0,26) =2,2 .. . 4,4.
Заметим, что этот множитель не имеет решающего значе
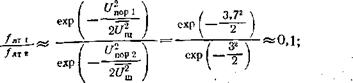
ния* уж очень резкая зависимость частоты ложных тревог от порога Упор, так чт0 незначительное увеличение порога (на б 23%) позволяет снизить частоту на порядок:
|
|
Отсюда вытекает и другой важный вывод: ложная тревога на интервале наблюдений Т, как и при единичной выборке, зависит прежде всего от выбранного порога — соотношения UaQp}'Umi и в значительно меньшей степени от частоты /хар.
Подведем итог. Чтобы принять решение о наличии или отсутствии сигнала, смесь сигнала с шумом с выхода линейного тракта необходимо подать яа решающее (пороговое) устройство. Если поданное напряжение превышает некоторый порог срабатывания (Лор, это устройство принимает решение «сигнал есть». Выбросы шума приводят к ошибкам. Когда шумовой выброс больше [/пар, то даже в отсутствие сигнала принимается решение «сигнал есть». Это ошибочное решение называют ложной тревогой.. Вольтой отрицательный выброс, накладываясь на сигнал, может уменьшить напряжение ниже уровня порога срабатывания — тогда принимается ошибочное решение «сигнала нет» (пропуск цели). Вероятности ложной, тревоги Рлт и пропуска цели Рл? относятся к основным критериям качества обнаружителя. Чем больше отношение напряжения порога срабатывания к шуму и„ov/Um, тем меньше вероятность Рлт, чем больше отношение - сигнала (его амплитуды) К порогу UCA. lUnop, тем меньше вероятность Рпр. Так приходим к основной задаче разработки ФПУ — максимизации отношения сигнал-шум Uca/U^i.
В оптико-электронных системах вероятности ошибок Рлт, Рпр, как правило, не должны превышать значений 10-3... 10~9, что обеспечивается при... 12 и £/ИОр== (3 ... 6)t/ш - Как видим, вариация отношений Uca/Uh,, UnopJUm в ФПУ относительно мала—это объясняется очень резкой зависимостью вероятностей РЛт, Рпр от указанных отношений.
Когда момент возможного прихода сигнала точно известен, то достаточно взять один отсчет в момент достижения сигналом своего максимума. Если же момент прихода сигнала заранее не известен и он может прийти в любой момент временного интервала Т, то в течение Т приходится брать - Tlx кор отсчетов (ткор — время корреляции), поэтому вероятность возрастает в это же число раз Г/ткор. Чтобы исключить зависимость от интервала Т, число шумовых выбросов NaT относят к единице времени — вводят частоту ложных тревог ?дт=Л^лт/Г=Рлт/7’.