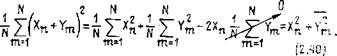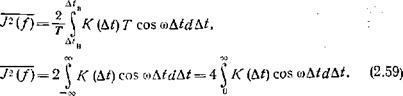Фотоприемные устройства и ПЗС. Обнаружение сла­бых оптических сигналов

ОСНОВНЫЕ ПРЕДСТАВЛЕНИЯ О ШУМОВОМ ПРОЦЕССЕ

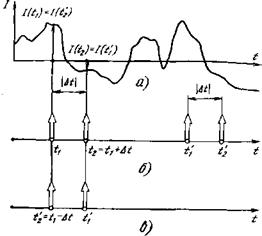
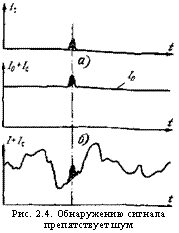
Шум как случайная функция. Пусть в цепи ФП (входной цепи усилителя) течет только фототок импульсного сигнала (рис. 2.4,а). Тогда при достаточном усилении в принципе мож­но обнаружить любой, сколь угодно малый сигнал. Однако во входной цепи кроме сигнального течет еще постоянный ток / (§ 1.2). Предположим сначала, что этот ток строго постоянен, 1 = 10 (рис. 2.4,6). и в этом случае можно теоретически обнару­жить сколь угодно малый сигнал — достаточно вычесть посто­янную составляющую тока /0. Однако такой случай умозри­телен — вследствие дискретности заряда ток всегда флуктуирует (рис. 2.4,э). К флуктуации тока ФП добавляются флуктуа­ции от других источников. Флуктуация тока и является поме­хой, мешающей обнаружить сигнал: малый сигнальный им­

Пульс можно не отличить от шумового выброса, как это й
изображено на Рнс - 2.4, я.

Не было бы шума, не было бы предмета теории обнаружения.

Функция / (0 может быть произвольной формы. Такая функция называется случайной £52 54]. Для ее описания вво­

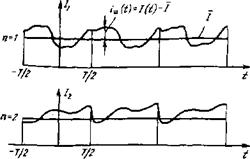
Дят понятие ансамбля сово­купности большого числа со­вершенно идентичных систем (в нашем случае ФПУ), находя­щихся в совершенно идентичных условиях. Будем наблюдать за током во входной цепи этих ФПУ (током ФП) в течение вре­мени Т. В первом ФПУ получим некоторую произвольную функ­цию Л (0* В0 втором — функцию /2(0> в ФПУ тг-го номера функ­цию /*(/) (рис. 2.5). Эти функ­ции 1 п(0, п = 1, 2,..., называются реализациями случайной функции 1(1) на интервале наблюдения Т. Выберем значение случайной функции в некоторый момент времени Это зна­чение /(/*) является случайной величиной. Простейшие стати­стические характеристики случайной величины — моменты по­рядка т. е. ее значение в степени I, приходящееся в среднем на каждую из выборок:

N

(2.20)

Если в дальнейшем над какой-либо величиной (/, £/ш2) встретится черта, надо помнить: такая простая с виду черта обозначает утомительные операции сложения всех выбранных значений (в соответствующей степени /= 1, 2, ...) и деления на число слагаемых. Момент первого порядка тока / (*) есть его среднее значение. В стационарных условиях среднее по ансамблю значение /(£ 1) не зависит от времени выборки Ни) ~1 = соп5{. Когда в § 1.2 говорили «постоянный ток», име­ли в виду постоянство его среднего значения.

Под шум 1ш будем понимать отклонение случайной функции от своего среднего значения:

1'ш = /(*)—7. (2.21)

Такую функцию называют центрированной: значение случайной величины в любой из моментов времени отсчитывается от сред­
него («центрального») значения I. Поскольку мы уже вычли среднее значение 7, то среднее значение центрированной функ­ции (шума г'ш) обязано равняться нулю:

..ТІГГТтттт^

Іші

Шх

*шш I

*шт

*■»#

П-Н

Е)

#т

Б)

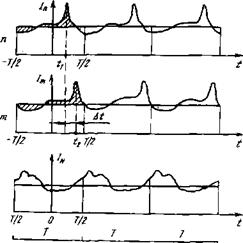
Рис. 2.5. К. понятию ансамбля: а — реализации шума в системах ансамбля; б — спектры реализации? в — те же реали­зации - в одной системе. Изображения условны.

(2.22)

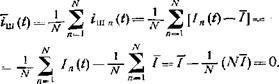Спектр шума. Шумовую реализацию 1п (£) на интервале интервале (—772, Г/2) точно так же, как и сигнальный им­пульс ЕсЬ), можно разложить на гармоники. Поскольку Лг(0 — функция произвольная, то в отличие от (2.6), которая записана для симметричного сигнала, надо учесть не только косинусоидальные 1пс{!), но и синусосоидальные 1Па(!) состав­ляющие спектральной плотности:

Следующим шагом должен быть расчет статистических па­раметров — моментов. Чтобы рассчитать моменты, надо воз­вести амплитуду гармоники в степень / (2.20). И здесь сталки­ваемся с определенными затруднениями: спектральная плот­

Ность реализации, полученной для конечного интервала наблюдения, оказывается «размазанной» по интервалу частот, так что амплитуда гармоники любой строго фиксированной частоты равна нулю. От нуля отличен лишь цуг гармоник М/М/ cos 2n(f+df)t, занимающих некоторую конечную полосу частот Д/. Но вряд ли такой цуг можно рассматривать как гармонику, так как при временах kfOn он всегда расходится. Поэтому для наглядности дальнейших расчетов проделаем с нашей реализацией следующую манипуляцию: репродуцируем ее без изменения бесконечное число раз, как это показано на рис. 2.5, а. Пусть не смущает такая условность модели: в даль­нейшем от нее освободимся, устремив время наблюдения Т к бесконечности. А сейчас благодаря проделанной манипуляции получим реализацию, которая пунктуально повторяет свои зна­чения через период Г, 1шп(0 =w(^— Г). Поэтому в ее спектре сохранятся лишь те гармоники, которые тоже повторяют свои значения, cos a>t = cos <±> (t—Т), т. е. гармоники с периодом Т [50, 511:

Nlf = T, /=1/Г, 2/Г, 3/Г, 4/7-, S/Г........ п/Т.

Как видим, на каждый интервал частот Д/=1 /Г приходится теперь одна гармоника, что и отражено в спектре рис. 2.5, б. Плотность непрерывного спектра /п(/), полученная раньше для реализации Іп(і) на конечном интервале Т и приходящаяся на эту полосу Д^ как бы стягивается и определяет амплитуду гар­моники ішп (0:

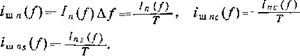(2.25)

Нам удалось сконструировать периодическую реализацию *шп(0 и ПОЭТОМУ получить ДЛЯ нее дискретный спектр 1тп{!). Дискретность спектра дает возможность рассчитывать стати­стические параметры — моменты, так как позволяет возводить гармонику строго фиксированной частоты в любую степень

*'шл С057((й/4-ф).

Прежде всего постараемся найти момент первого порядка — Средние значения спектров *ш(/), (шсИ), £шя(/). Усредняя по ансамблю спектр (2.23), (2.25), получаем

N

Достаточно было поменять порядок суммирования и интегриро­вания, чтобы увидеть, ЧТО среднее значение спектра 1шс(!) яв­ляется спектром среднего значения шума £ш(0. Но поскольку среднее значение шума равно нулю, то и среднее значение спектра оказывается равным нулю! Точно так же ^(И—О,

М/)=о.

Попытка рассчитать среднее значение спектра окончилась неудачей: получили неинформативный нуль. Отличен от нуля момент следующего, второго порядка — средний квадрат, по­скольку суммируются положительные квадратичные члены. Не представляет труда согласно определению (2.20) записать сред­ний ^квадрат амплитуды 1ш2(/)- Итак, нам вплотную удалось подойти к цели настоящего раздела — определению спектра шума. При этом надо не только записать выражение для среднего квадрата 1ш2(/), определить спектр шума, но и свя­зать его со средним квадратом отсчета шума в любой момент

Времени 1'ш2(0' Для этого придется предварительно провести несколько дополнительных выкладок. Выделим во временной реализации iwn (0 гармонику одной строго фиксированной ча­стоты :

Turn (0 = cos imnB sin (2.27)

W(0=^cos (2.27a)

Сначала будем оперировать с первым из этих двух представ­лений (2.27). Возведем его в квадрат и усредним по ан­самблю:

1ш (t) = i ш с (/*) COS <akt + / ш, (/*) Sin C0jfeif]2 =

= 4 с (fk) COS2 tokt - f ii s(fk) sin2 &kt +

+ 2^ш c (/*) гш л (Л) cos оkt sin <aft*. (2.28)

Для дальнейших преобразований необходимо найти связь меж­ду членами, в которые входят составляющие спектра гшс(/а), iuis(fk)~ Пока нам известно о шуме только одно — он стацио­нарен. Значит, все моменты времени равноправны. Пусть в я-й реализации в некоторый момент t наблюдается зна­

Чительный выброс (рис. 2.5,а). Но чем хуже момент време­ни ^2? Значит, с той же вероятностью можно встретить т-ю реализацию такой же временной формы, но сдвинутую по ОСИ времени, =imn{t—At), At=t2 — tu ТЭК ЧТО ШуМОВОЙ

Выброс придется уже на момент i2 (см. рис. 2.5, а, при п = т). Как было показано в § 1.3, в этом случае спектры отличаются только фазой, ф = о)Дt, а сами амплитуды одинаковы, гштп = iuin{fk). Из этого рассуждения следует, что в ансамбле можно выделить подансамбль систем с одинаковыми амплитудными спектрами imn(f), но со случайной фазой ф, равномерно меняю­щейся во всем диапазоне возможных значений (—л, - f-я). Ис­пользуем (2.23), (2.25) и выполним усреднение по фазе в та­ком подансамбле:

Ьшпс (/*) = [*ш „ (/ft) COS ^]2 = 4 п (/*) COS2j3 = 1ш п (/к)12,

4 я* (/ft) — [imn(fb) Sin^]2= il п (fk) Sin2ij5 = U n (f *)/ 2,

Ns (f к) =■ ini nc (/ft)» (2.29)

^iu nc (f k) ^*iu ns (f k)=z f^m n (f h) COS n (f ft) Sin tj)j =

= imn(f k) sin 2^/2=0. (2.30)

В формулах (2.29), (2.30) учтено, что при указанных из­менениях фазы функции cos2iЈ, sin2^ меняются в пределах

0. .. 1 и их среднее значение равно 1/2 (вспомним, что такое значение встречается в электротехнике при расчете действую­щих значений гармоник).

Соотношения (2.29), (2.30) достаточно очевидны: вследствие случайности шумового процесса составляющие спектра 1Щпс> iuinsif) Равноправны, что и отражает (2.29). Если эти составля­ющие независимы, то, как будет показано ниже, всегда выпол­няется условие (2,30). С учетом полученных выражений фор­мула (2.28) сразу упрощается:

4 (0 = il С (/) (cos^ сat + Sin2 &£) = 47(7) = &Л7). <[3]’31)

Отметим, что вклад синуса и косинуса в щум в среднем во времени одинаков:

С (/) COS^ (tit — с (^)/2»

(2.32)

Ности, то это значение нэдо разделить на полосу частот = !Т (2.24), которую эта гармоника занимает. Так получим спектральную плотность мощности шума

(2.35)

Спектральная плотность У2 (Я оПределЯется при Т-> оо; в этом случае Д / = 1 / 71 0 и функция №{/) становится непрерывной-

При преобразованиях (2.35) воспользовались ранее полу­ченными формулами (2.25), (2.34), а также формулой (2.37), которая будет доказана ниже. Для спектральной плотности мощности шума широко используется еще одно соотношение, которое получается при подстановке в (2.35) выражения для спектра реализации (2.23):

Все приведенные формулы для спектральной плотности мощ­ности шума очень полезны. Они определяют ее либо через действующее значение гармоники сконструированного дискрет­ного спектра 4 (/)/2> либо через спектральную плотность 7Ц/) шумовой реализации, которую наблюдаем на интервале Т» либо через саму эту реализацию /ш (() = I (р — / и, наконец,

Связывают со средним квадратом шума 4(/) в некоторый момент времени.

Спектральная плотность мощности шума, или спектр шума, является одной из основных характеристик шумового процесса в радиотехнических устройствах. Ниже будет показано, что этой характеристики в большинстве случаев достаточно для расчета остальных параметров шума.

Сделаем одно замечание относительно термина «мощность». Конечно, термин условен: речь идет о флуктуации не мощности, а квадрата случайной величины (в данном случае тока). Так, чтобы перейти к электрической мощности от спектральной плотности мощности токового шума, надо умножить ее на со­противление цепи, по которой протекает шумовой ток. Усред­нение квадрата привело к тому, что спектральная плотность мощности шума представляет действующее значение шумового тока (множитель 1/2 в формулах (2.34), (2.35) при квадрате амплитуды ;ш2(/).

Эргодичность. Измерение спектра. Из приведенного опре­деления спектра шума следует, что для его измерения, каза­лось бы, нужен ансамбль из большого числа ФПУ. К счастью, это не так: в реальных стационарных системах, в том числе и ФПУ, шумы как правило, эргодические, для них усреднение по
ансамблю можно заменить усреднением во времени. Для эрго - дических процессов те же N реализаций случайной функции на отрезке времени 7 можно получить уже не параллельным на­блюдением за ними в ансамбле N идентичных устройств в те­чение этого интервала времени Ту а при последовательном на­блюдении только за одним устройством, но соответственно в те­чение большего времени 7-х = N7 (сказанное иллюстрируется рис. 2.5, в). Тогда измерение спектра шума проводится на од­ном ФПУ следующим образом:

1. Выбираем фильтр с резонансной частотой и узкой поло­сой А/. На выход фильтра проходит одна гармоника частоты

Полоса Д/, как мы видели, соответствует интервалу наблю­дения Т. Значит, через эти интервалы времени на вход фильтра поступают разные реализации с различными спектрами, поэто­му и амплитуды гармоники [к будут соответственно принимать значения £ш1(/й), 1ш2(/а:) ■ ■ • (рис. 2.5,6).

2. Используя далее квадратичный детектор с постоянной

Времени интегрирования 7Л~, усредняем квадраты на всем ин­тервале наблюдения 7х, т. е. по всем Л7 = 7x17 —7х&1 выбор­кам. Чем больше интервал Тдг = N7, тем ближе измеренное зна­чение к истинному спектру шума которое определяется

При 7-^оо. Для получения спектра шума нам уже не нужен ансамбль, а нужен всего один «солист» — всего одно ФПУ.

Линейные преобразования случайной функции. В линейных системах (например, в линейных цепях ФПУ) с первичными источниками шума выполняются две основные операции — ум­ножение на константу и сложение. Опять выделим в п реали­зации входного шума гармонику частоты /V Это шумовая гар­моника преобразуется точно так же, как детерминированная гармоника сигнала. Например, падение напряжения от проте­кания шумовой гармоники 1юп(!к) находится ее умножением на нагрузку Z, иШЛуп {!к) При прохождении через усили­

Тель шумовая гармоника умножается на коэффициент переда­чи, ишп (/&) = К1шп (!к) - Нели в линейной цепи действуют состав­ляющие от нескольких источников, то эти составляющие скла­дываются.

Средний квадрат произведения случайной величины X и константы К, а также средний квадрат суммы двух случайных величин X, У находятся с помощью следующих известных пра­вил [54].

1.

При умножении на константу случайной величины ее средний квадрат умножается на квадрат константы:

(/сх)2=/оа:2.

2. При сложении случайных независимых центрированных величин их средние квадраты складываются:

(2.38)

Приведенные правила следуют из определения среднего квадрата (2.20) при 1 = 2. Поскольку К2 — одинаковый множи­тель для всех слагаемых, то его можно вынести за знак сум­мы (2.20) и непосредственно получить формулу (2.37). Не­сколько сложнее расчет для суммы случайных величин. Пусть в N реализациях случайная величина принимает последовательно значения Хп, п — , 2,..., N (наиболее вероятные значения встречаются чаще). При их суммировании к каждому первому слагаемому Хп с данным номером п может прибавиться любое второе слагаемое Ут с любым номером т: ведь мы специаль­но оговорили, что значение Ут не зависит от значения Хп. По­этому для каждого номера п получим N возможных сумм Хп-~Утп, Поскольку п пробегает N значений, то

Всего получим IV2 сумм с разными номерами (пт). Квадрат каждой суммы равен

(^пЧ-7»)2 = ^п2+Ут2+2Х„Ут. '(2.39)

Проведем сначала при фиксированном п усреднение по тл

Здесь учтено, что среднее значение случайной величины У рав­но нулю, поскольку она центрированная. Усреднив далее по п, перейдем от (2.40) непосредственно к выражению (2.38). Правило (2.38) распространяется на любое число независимых слагаемых.

В начале этого раздела приводился пример умножения: на­пряжение шума связывалось с токовым шумом соотношением

^шв хп (М — ^вх^шп (Iк) , Ушп (к)=К1:шп(Ы). (2.41)

Теперь с помощью (2.37) найдем связь между средними квад­ратами этих величин:

UUf*) = K4l{ft). (2.42>

Оба указанных правила для линейных преобразований случай­ных функций придется еще неоднократно использовать в даль­нейшем, да и в предыдущих разделах они активно использова­лись. Так, правило сложения применено в формулах (2.28), (2.31), в которых X = imc{f) cos (о/, Y=ims(f) sin (at. Правило умножения было использовано при выводе формулы (2.35), в которой X — 1(f), К= IJT.

Выборка текущего значения шума. При обнаружении наблюдаем конкретную зависимость шума от времени іш(0*

Величина шума (тока, напряжения) в некоторый фиксированный момент времени гш(^,) называется выборкой. Найдем ее связь со спектром шума 7ц/). Для этого вернемся к модели, сконструированной в разделе «спектр шума». Там нам удалось временную реализацию шума гш(*) разложить на гармоники ДискрЕтных частот /=/к со средним квадратом амплитуды

*ш(/а) и соответственно действующим значением *ш(/й)/2. Было показано, что вклад каждой гармоники в средний квад­рат шума в любой момент времени равен действующему значению этой гармоники (2.34), (2.35):

4м=(Ж(75)/2=7ч/«)д/. (2.43)

Спектральная плотность мощности шума появилась в этой формуле согласно своему определению: ведь она была введена как действующее значение гармоники, но отнесенное к полосе А/, которую эта гармоника занимает (2.35). Последователь­ность дальнейших действий напрашивается сама собой: по­

Скольку шум (£) представляет собой сумму независимых гар­моник частот /*, то для нахождения среднего квадрата надо сложить средние квадраты гармоник — их действующие значения:

2

Т„(/)=?„= 2 _Ц«== 2 Тч73Д/= 7чГ)<1/. (2.44)

Замена суммы на интеграл также вытекает из определения спектра шума (2.35), который должен находиться на интерва­ле наблюдения Тоо, Д/= 1 /Т—► 0. Таким образом, площадь спектра шума однозначно определяет средний квадрат значения шума в любой момент времени.

Средний квадрат центрированной случайной величины (а таковой и является шум) называют дисперсией и обознача­ют о2. Часто используют еще один термин — среднеквадратич­ное значение (не путать со средним квадратом!). По определе­нию среднеквадратичное значение есть

V4 (2,45)

Размерность среднеквадратичного значения совпадает с раз­мерностью самой случайной величины — в данном случае тока.

Две выборки шума. Поскольку длительность сигнала Тс конечна, то одной выборки явно недостаточно, необходимо иметь информацию о шуме на отрезке времени порядка не­скольких Тс. Так возникает необходимость рассмотреть сосед­

Ние значения шума в соседние моменты времени іи Как всегда, первый шаг — расчет среднеквадратичных значений. Но новой информации здесь не получим, ведь только что было показано: для стационарных эргодических процессов средне­квадратичные значения не зависят от времени,

VЙ,(<,) =гш.

В чем же новизна постановки задачи двух выборок? Обратим­ся к рис. 2.6, где представлены реализации двух случайных процессов. В процессе на рис. 2.6, а, и на рис. 2.6,6 в мо­менты і и І2 с равной частотой повторяются два возможных значения «1» и «—1», так что среднеквадратические значения для обоих проценссов в оба момента времени одинаковы;

Vlmih) =У &(f2) =уЛ1|3-12 + 3 (- 1)2] = 1. (2.46)

Но как различны эти процессы! В первом процессе (рис. 2.6, а) появление в момент значения «1» или «—1» обя­зательно влечет за собой то же значение и во второй момент времени Два события, детерминированно связанные между собой заданным функциональным соотношением (в данном слу­чае 1Ш(4) =/ш(Л)), называются полностью коррелированными.

Во втором процессе (рис. 2.6, б) ситуация совершенно иная: случайные события £Ш(Л) и im{h) не коррелированы, т. е. ни­какой связи между появлением значений «1» и «—1» в момен­ты времени ti и /2 нет. Так возникает необходимость ввести меру статистической взаимосвязи двух выборок в моменты il и 4 —Функцию корреляции K(tu t2).

Функция корреляции. Эту функцию конструируют по ана­логии со средним квадратом: для одной выборки (одномерной случайной величины) имели одно значение 1Ш(4) и его умно­жали само на себя, Теперь есть две выборки

*ni(*i)» *ш(4) (двумерная случайная величина), так что перем­ножают значения этих двух выборок. Потом проводится стан­дартная операция усреднения:

К (tv t2) = K (At) = 1Ш (*j) im {t2) = гш (0) im (*1 + М). (2.47)

В стационарном шумовом процессе (в узком смысле) все его статистические характеристики не зависят от времени —в данном случае от tt. Это и дало нам право записать функцию корреляции как функцию только аргумента At. Располагая вы­борки tu t2 произвольно на оси времени, будем получать одно и то же значение функции К, если постоянен интервал между выборками (рис. 2.7, а, б). Стационарность обусловливает и свойство четности функции корреляции; проведя замену

= —At, получим

К (- ДО - й^г'ш^-ДО = UV-гД0UV) = к (АО • (2.48)

Четность К {At) видна также из сопоставления рис. 2.7, б, в. На рис. 2.7, в взяты выборки t2'<ti/, At=t2'—//<0. Посколь­ку функция К не зависит от абсолютного положения выборок

T^ на оси времени, то эти выборки совмещены с выборками tu 4- Поэтому произведение выбранных значений и совпадает в каждой реализации, гш(4Нш(4) =im(4/)im(4/).

Большие значения функции /((ДО говорят о высокой степе­ни корреляции выборок. При Af-И) две выборки по существу

Проводят в один момент времени, они, естественно, полностью коррелированы, 1Ш(Л) «1ш([4]А), и функция корреляции дости­гает своего максимального значения, равного дисперсии:

К (0) = lim гш (*,) i„ (ti - f М) = 4 (<,) = = 02. (2.49)

4*^0

Когда выборки не коррелированы (At-+oo), то независимо от значения первой выборки im» (Л) будем получать во второй вы­борке любое из возможных для нее значений immU2) • Зафикси­ровав значение первой выборки [5]Шп(^), усредним сначала про­изведение £Шп(М>0*шт(*2) П0 всем возможным значениям вто­рой выборки:

/V

*шт(^) = ^шП(^)^ш^2) = ^шЯ*0. (2.50)

M= I

Чтобы получить корреляционную функцию, надо было бы про­изведение imn(ti)lm(h) усреднить ПО ПврВОЙ Выборке, НО ЭТО произведение при любых tninUi) равно нулю, так что

Д*-*оо, К(М) = 1шу i)imUi + AO = 0. (2.51)

Таким образом, функция К(Д?) действительно является ме­рой взаимосвязи (корреляции) случайных величин: она прини­мает максимальное значение, когда выборки полностью корре­лированы (Д£->-0), и спадает до нуля, когда они статистически независимы (Д^-мэо*). С учетом отмеченных свойств на

Рис. 2.8. Время корреляции—это эффективная дли­тельность корреляционной функции

Рис. 2,8 приведен ТИПОВОЙ пример корреляционной функции. Ее можно рассматривать как симметричный импульс. Эффек­тивную длительность такого импульса можно назвать временем корреляции и определить ее по прежней методике, аппроксими­ровав функцию К(М) прямоугольником (рис. 2.8). При этом приравниваются амплитуды и площади импульсной функции (в данном случае К(ДО) и ее прямоугольной аппроксимации. Длительность прямоугольной аппроксимации и принимается за время корреляции:

Оо

^ /г (до Л{Ы).

Выбор термина «время корреляции» понятен: если будем про­водить выборки I на интервале тКОр (от —ткор/2 до ткор/2), то выбранные значения коррелированы, так как К=о2. При рас­стоянии между выборками |4—41 = [Д^| ;>тКор/2 выбранные значения уже будут независимы, так как /С—0.

Корреляцию между выборками шума 1'ш(*г) обяза­

Тельно надо учитывать при их дальнейшей обработке в ФПУ, Так, если эти выборки складываются (как, например, в нако­пителе), то для дисперсии суммы имеем

(^і) - Ь*ш (*г)]2— іш (^г) 2/ш (^) гш (^г)

-

2/ш -{- 2 £ш (^) іш (£2)*

SHAPE \* MERGEFORMAT

Отсюда при «близких» выборках

1^2 ^і|^тНОр, гш (^) гш (^2) = £ш>

А при «далеких» выборках

1^2 ^іі^^кор» Іт (4) Іт (^2) — 0,

Кяк вилим дисперсия суммы изменяется в два раза. Это же пмчяйтся и ИЗ сформулированных выше Правил линейных ппробпазований случайных величин. Согласно (2.38) дисперсия независимых величин равна сумме дисперсий, что дает сум ы Сложение полностью коррелированных и одина­ковых слагаемых £Ш(Л) = 2*ш(^) равносильно умноже-

” ня коэффициент 2, дисперсия при умножении увеличи­вается согласно (2.36) в /С2=4 раза, что совпадает с (2.54).

Спектральная плотность мощности шума — это спектр функ­ции корреляции. Таким важным соотношением оказываются связанными между собой две основные статистические харак­теристики шума. Физический комментарий этого замечательно­го свойства дадим ниже. А сейчас выведем эту зависимость Гтеорему Винера—Хинчина) [52] непосредственно из формулы (2.36), определяющей спектр шума. Для этого перейдем в ней к двойному интегралу:

TOC o "1-5" h z

'IZ "1 im (^) cos (3st]dLt /ш (^2) cos I=

■Г/2 - Г/2 J

§ jj іш г’^2) cos 0)t2 cos (X)tldtxdt2- (2.50

—T/2 ~Tj2

Далее заменим переменную t2 на переменную kt=t2—t: т ц

J4f) = Y - j jj М*і)М*і + Д*)Х

-Г/2 дt

COS ыДЛ

X

(AtR Г ТІ2

■у К К (АО ^ (cos —cos(2w^-]-A/))flff,

---- Т! 2

I Т/2

Здесь использовано определение функции корреляции (2.47) и установлена последовательность интегрирования. Сначала ин­тегрируем по til

~ Г/2

Jj (cos о)А^ — cos (2(з)іг - f-&t))'dti

—Т/2

Г/2

= (cos to А^) ^—sm (2<^> + j I

-Г/2

- T COS ^ А/ — № + Al) sin (шг -b AQ T cog

(2.58)

Поскольку интервал наблюдения выбирается большим, второе слагаемое пренебрежимо мало и поэтому его опускаем. Подставляя найденный интеграл в (2.57), получаем

При большом интервале наблюдения пределы интегрирования д/в= (4)в_ 4 = 7/2—4; Д*н = (4>)н-4=—Г/2—4 (2.60)

Много больше (по абсолютной величине) постоянной затухания подынтегральной функции (за исключением малых областей на краях диапазона 14 I > I Г/2—тКор1, вклад которых в общий ин­теграл несуществен). На этом основании мы и перешли к бес­конечным пределам. При преобразовании в (2.59) учтено также свойство четности /С(Д0- Так получена искомая связь между

Р(!) и/с(ДО.

Отметим, что из (2.59) однозначно следует обратное фурье - преобразование:

Со

К (ДО = (/) СОБ <0Ш/.

Полученное раньше выражение (2.44) для дисперсии как пло­щади, ограниченной кривой спектра шума Я (И, является лишь частным случаем общего выражения (2.61) при Д£ = 0.

Функция распределения. Рассмотренных выше статистиче­ских характеристик (дисперсии, спектра шума, функции кор­реляции) недостаточно для обнаружения сигналов. Случайная функция — шум /ш(0 —может принимать в интересующий нас момент времени 4 произвольное значение, так что необходимо знать вероятность его появления. При большом числе систем N в ансамбле (Л^-^оо) выборки /ь /2, . - - /л начнут

Повторяться. Получим только М разных значений /ь 1и> • - • • • •, Лп,.. ., 1М> М<ЛГ. Каждое из значений 1т будет встре­чаться раз (при непрерывной величине /(4) значение пт относят к диапазону /т. .. (7т-1-Д/)), причем 2пт~М. По опре­делению функция распределения — это вероятность (частота) появления данного значения 1т (1т.. .

Р (1т) Д/ = пт/Ы,
функция распределения (плотность вероятности р(/)5 являет­ся полной и достаточной статистической характеристикой слу* чайной величины (но не случайной функции). С ее помощью можно рассчитать все остальные характеристики, в том числе момент любого порядка, включая дисперсию. Так, группируя в выражении (2.20) члены с одинаковым значением тока, по­лучаем

I1 = ■ • ■ 4" 1п + • • ■ + ^А') =•

= 77” ""Ь + • * ’ Л~(гт1т'Ь • * ■ +Яд|/м) ~

М М оо '

=2^/»=2р(/„)/и/-> ? р(л/'^/. (2.64)

Т=1 т= I _оо

Однако решение обратной задачи (нахождение вероятности любоф значения I по заданной дисперсии о2) возможно лишь тогда, когда известная функция распределения и в качестве параметра в нее входит только а2. Именно такую ситуацию имеем в большинстве радиотехнических систем, шумы кото­рых подчиняются нормальному закону распределения [53]:

Р(г“)=у1Ь-еХР(-2^)' (2'65)

Нормальный закон называют часто законом больших чисел: теория показывает, что при суммировании большого числа не­зависимых одинаково распределенных случайных величин рас­пределение суммы нормализуется при любом законе распреде­ления для слагаемы к (элементарной флуктуации), поэтому нормальный закон и является универсальным. Шумовой про­цесс давно слился в нашем сознании с нормальным за­коном: в большинстве задач этот закон подразумевается сам собой, поэтому когда говорят о шуме, обычно имеют в виду его спектр Р([) либо площадь этого спектра —

1 /Т

Дисперсию а2, среднеквадратичное значение 1Ш = у /щ =|/о2, что вполне достаточно для описания нормального закона. ФПУ не является исключением: теория обнаружения оптических сиг­налов также базируется на нормальном законе. Но нельзя за­бывать и о возможных отклонениях от нормального распреде­ления, когда отдельные флуктуации становятся различимы­ми— не накладываются друг на друга, и закон больших чисел не действует. Так, в ФП могут наблюдаться взрывные шумы [55, 56], а в ЛФД и микроплазмы, обусловленные бистабиль­ными состояниями локальных областей р-я-перехода [57—59}. Случайные переключения из состояния «выключено» в состоя­ние «включено» приводят к появлению импульсов со случайной длительностью и, как правило, с фиксированной амплитудой.

Задача разработчика прибора устранить эти шумы. Другой случай отклонения от нормального закона — предельно малый уровень токов, столь малый, что становится возможным регист­рировать каждый электрон в отдельности. На этом подробнее остановимся в § 4Д 4.4,

Для задач настоящей книги выражения для распределения вероятности одной выборки /(^1) будет достаточно. Ради обще­го представления о шуме надо, однако, отметить следующее. При двух выборках /(^), IЦ2) будем иметь уже двумерную случайную величину, поэтому закон распределения станет тоже двумерным, в формулу этого закона входит не только диспер­сия, но и функция /С{^2—и)- Однако непрерывная случайная величина — это не одно и не два значения, а бесконечное число случайных значений (выборок) на интервале наблюдения Т, так что в принципе для ее описания требуется бесконечномер­ная функция распределения (с бесконечным числом аргументов /(О)- Реальные шумовые процессы имеют конечное время корреляции Ткор; на этом отрезке времени значение случайной функции можно считать постоянным, поэтому «мерность» слу­чайной функции (число независимых отсчетов — число пере­менных) конечна, порядка Т(ткор.

Основные представления об источниках шума. Основными, принципиально неустранимыми источниками шума (и не только в ФПУ, но и в радиотехнических устройствах вообще) являют­ся дробовой, генерационно-рекомбинационный и тепловой шумы.

Дробовой шум возникает в приборе с областью простран­ственного заряда из-за дискретного характера носителей заря­да. Носитель («дробинка»), попав в область пространственного заряда, индуцирует ток во внешней цепи в течение времени Тпрол — всего времени, которое ему необходимо для пролета через ОПЗ (§ 1.2). Так во внешней цепи индуцируется импульс длительности Тпрол.

Генерационно-рекомбинационный шум возникает в ФР (и вообще в полупроводниках). По существу, это тоже дробо­вой процесс и даже два независимых дробовых процесса. Гене­рационный: «дробинки» (фотон или фонон) при своем погло­щении генерируют электронно-дырочные пары в объеме полу­проводника. И обратный ему рекомбинационный процесс: каждая из пар через некоторое время рекомбинирует, испуская фонон (или фотон). Пока пара существует (от момента генера­ции до момента рекомбинации), она увеличивает концентрацию и, следовательно, ток. Таким образом, генерация и рекомби­нация пары приводят к импульсному приращению тока. Дли­тельность этого импульса случайна, ее среднее значение есть среднее время существования генерированной пары в полупро­воднике, т. е. время жизни Тж.

Физическая природа теплового шума также отражена в его -

Названии: тепловое движение носителя в проводнике (полу­проводнике) может нарушить электронейтральность, возникает локальное поле и локальная ЭДС. Пусть в резисторе посто­янного сечения Л один электрон сместится на некоторую дли­ну I. Слой этой длины обладает емкостью С. Тепловое смеще­ние электрона можно рассматривать как перенос заряда ц с с одной обкладки этой емкости на другую — как зарядку емко­сти. Время разрядки определяется емкостью и сопротивлением указанного слоя

= р 1(А, С —ее<И/А /?С = рево = тдг. (2.66)

Таким образом, релаксация не зависит от геометрии и опреде­ляется физической константой материала — максвелловской по­стоянной времени хм (удельным сопротивлением р, диэлектри­ческой проницаемостью еео)-

Все рассмотренные источники шума дают мгновенные стати­стически независимые элементарные флуктуации; система от­кликается на такое короткое воздействие — появляется элемен­тарный импульс, релаксирующий с характеристической посто­янной времени этой системы Тш. В ФД для импульсов дробового шума эта длительность равна тПрол, в ФР для гене - рационно-рекомбинационного шума тж, для теплового шума тм - При прохождении шума через электрические цепи и усилители на величину тш влияет постоянная времени этих радиотехни­ческих трактов.

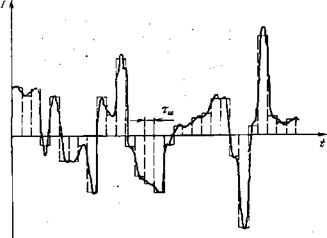
Элементарные шумовые импульсы, случайным образом на- кладываясь друг на друга, дают случайную функцию £ш(0 (рис. 2.9). Если моменты прихода большого числа элементар-

П

Ных импульсов будут достаточно близки, то в шумовом процессе вы­делится суммарный импульс боль­шой амплитуды. Его эффективная длительность не может быть Коро­че составляющего элементарного импульса тш. Аппроксимируя, как всегда, такие суммарные импульсы прямоугольниками, получаем для шума аппроксимацию в виде по­следовательности импульсов сред­ней длительности Тш и случайной амплитуды (рис. 2.9). Конечно, эта аппроксимация весьма условна, ряд особенностей шума в ней поте­рян: не учтена флуктуация дли-

Рис. 2.10. Представление функции корре­ляции как шумового импульса, усреднен­ного по всем его равновероятным положе­ниям на интервале наблюдения Т

Тельности импульса и его формы, пренебрегается наложением импульсов и т. д. Вместе с тем эта аппроксимация приемлема для больших флуктуаций, которые особенно опасны: такие флуктуации редки и разделены между собой, интервал между большими импульсами в аппроксимации случаен (рис. 2.9). Не надо сетовать на «прямоугольность» нашего мышления: даже такая условная «прямоугольная» аппроксимация шума позво­ляет наполнить простым физическим содержанием введенные выше статистические характеристики, а в дальнейшем поможет при выводе ряда положений теории обнаружения.

Прежде всего становится возможной простая физическая интерпретация корреляции. Выделим на интервале наблюдения один шумовой импульс некоторой амплитуды /а длительностью тш (рис. 2.10, а). Памятуя о свойстве эргодичности, найдем сна­чала дисперсию усреднением во времени:

77 2

;2 1

0* = 1ш = у

-Т/2

Теперь найдем функцию корреляции. Если бы импульс был детерминированным и его положение на оси времени было бы известно, то, поместив первую выборку в максимум сигнала (в начало отсчета на рис. 2.10, я), мы с помощью второй выбор­ки, варьируя ее сдвиг Д/, смогли бы измерить /(^+Д0- И это очень важно: при таких условиях функция корреляции — про­изведение /(^)^1+Д0—это просто импульсный сигнал (с точностью до множителя /(^)). Шумовой импульс случа­
ен — в рассматриваемом примере на рис. 2.10 случайно его по­ложение на оси времени. Поэтому произведение /(М/М+Д*) надо усреднить по всем возможным положениям импульса И в этом случае функцию корреляции можно трактовать как импульс (с точностью до указанного множителя), но теперь — как некоторый типовой шумовой импульс, усредненный по всем возможным случайным импульсам в шумовом процессе.

Выполним указанную операцию усреднения. Поскольку шу­мовой импульс с равной вероятностью может находиться в любой точке временного интервала Г, то при усреднении надо равномерно перемещать его вдоль оси времени, например слева направо. На рис. 2.10,6 выбран момент, когда оба от­счета стали отличными от нуля, а на рис. 2.10, в — последний из таких моментов. Как видно из этих рисунков, произведение /(/[)/(^1 + Д0 отлично от нуля и равно /а2 на интервале хш—Д£.. Поэтому

|Д<| <тш, К(М) = Щ1)Ц(1 + М) = ^=^-Г,^

(2.68)

Здесь использована формула для дисперсии (2.67). Из описан­ной методики расчета функции К(ДО следует, что эта функция зависит не от положения выборок — от времени 1;и а только от At (как и должно было быть) и что она четна (как и должно было быть). Полученная функция корреляции изображена на рис. 2.10, г. Форма усредненного по описанному правилу им­пульса— функции Л* (ДО—треугольная. Усреднение привело к размытию фронтов, однако эффективная длительность — время корреляции Ткор —для рассматриваемого прямоугольного им­пульса равно длительности случайного шумового импульса тш (в общем случае шумового импульса произвольной формы тш^тКОр<[2тш) • Удивительно простой оказалась природа кор­реляции: система помнит, хранит мгновенную флуктуацию в течение тш—Ткор, поэтому значения всех выборок на этом ин­тервале, приходящихся на один шумовой импульс, одинаковы. Через время Ткор ~ Тш импульс полностью релаксирует. Затем на время тш система будет напоминать следующую флуктуацию и будем получать новые независимые отсчеты и т. д.

Становится также понятным, почему спектр мощности шума Получается фурье-разложением функции корреляции (2.58). Ведь функция К (ДО —это некий средний шумовой импульс, так что ее спектр и есть спектр этих шумовых импульсов (мно­житель /(^) в функции К (ДО дает размерность квадрата ве­личины). Все сказанное остается справедливым, когда на ин­тервал Т приходят N независимых импульсов. Если эти импуль­сы одинаковы по форме и случаен только момент их прихода,

То в N раз увеличивается дисперсия и вместо (2.66) получаем <72 = АЧш/а2/7’. Если они различаются длительностью, то в функ­цию корреляции (2.68) и дисперсию (2.67) войдет их средняя длительность, а если амплитудой, то в выражение для диспер - сии войдет средний квадрат амплитуды /а2.

Шум и сигнал: единство противоположностей. Несмотря на антагонизм сигнала, который пытаемся обнаружить, и шума, .который мешает это сделать, между ними оказалось много об­щего.

1. Сигнал представляет собой импульс; и шум является если не импульсом, то последовательностью импульсов (импульсная случайная последовательность).

2. Сигнал описывается детерминированной функцией £с(0>

Его основные параметры — амплитуда Еса и эффективная дли­тельность Тс. Случайные шумовые импульсы описываются с помощью функции корреляции К(М), которую можно тракто­вать как среднестатистический шумовой импульс: амплитуда

К{0)—не что иное, как средний квадрат шумового импульса, а эффективная длительность функции К (Л/) (время корреля­ции Ткор) не что иное, как типовая длительность среднестати­стического шумового импульса тш-

3. В пространстве частот импульсный сигнал представлен своим спектром, соответственно шум представлен спектром своего среднестатистического шумового импульса, т. е. спек­тром функции КШ).

4. Площадь импульсов дает максимальную плотность •спектров:

Со

£с(/ = 0)=--2 ^ ЕМШ;

Со

ТЦ0) = 2 ^ К{М)(И.

И, наоборот, площадь спектров дает максимальное значение импульса (амплитуду сигнала и дисперсию шума):

(2.7!)

Оо

О2--/г(0)- уч7)л/.

Все эти выражения были получены выше (2.10), (2.12), (2.44), (2.49), (2.59).

Как видим, шум маскируется под сигнал: не останавливаясь ни на микросекунду, он непрерывно засылает в ФПУ свои им­
пульсы, пытаясь проникнуть под видом сигнала через все звенья в решающее устройство и заставить принять ложное решение.

При интерпретации шума как случайной импульсной после­довательности могут встретиться трудности, связанные с рас­ходимостью интеграла (2.72). Это прежде всего случай избы­точного низкочастотного шума вида /2оэ 1//, когда интеграл расходится в окрестности нулевой частоты. Другой случай — расходимость интеграла в области высоких частот (/^оо); при преобразовании первичных шумовых импульсов в электрон­ных устройствах могут усиливаться высокочастотные составля­ющие шума, можно получить /г оз/2 (§ 2.4). Конечно, в реаль­ных устройствах мощность ограничена, так что зависимости вида 12сор должны быть справедливы в ограниченном

Частотном диапазоне. Однако при таких зависимостях пре­небрегать формой шумовых импульсов, аппроксимировать их прямоугольником нельзя. Одной из задач теории низкочастот­ного шума является поиск возможной формы шумовых импуль­сов и механизма их возникновения, определение минимальной частоты, до которой простирается низкочастотный шум.

Источники шума на эквивалентной схеме. Как отмечалось, каждая отдельно взятая гармоника в реализации шума /Шя(0 проходит через электрические цепи точно так же, как гармони­ка детерминированного сигнала. Поэтому источник гармоники шума, как и гармоники сигнала, отображают на эквивалентной схеме генератором тока либо напряжения и при дальнейших преобразованиях используют обычную теорию цепей. Здесь есть два отличия от гармоники детерминированного сигнала. Количественно гармоника шума характеризуется не амплитудой (не плотностью амплитуды), а средним квадратом (или плот­ностью среднего квадрата амплитуды /2). При суммировании нескольких гармоник в одном элементе цепи используют пра­вило не алгебраического, а геометрического сложения (вспом­ним: дисперсия суммы равна сумме дисперсий). Это правило справедливо как для гармоник одного источника шума (они статистически независимы), так и разных источников (гармо­ники одной частоты разных источников могут быть коррелиро­ванными; в наших схемах такие случаи встречаться не будут).

Строгое изложение теории шума радиотехнических систем читатель может найти в соответствующих разделах обширной литературы по статистической физике, радиотехнике, математи­ческой статистике [52—55, 60]. В настоящем параграфе приш­лось пожертвовать строгостью выкладок ради наглядности ин­терпретации основных статистических характеристик шума; представленная качественная модель шума как наложение среднестатистических импульсов будет «работать:» на нас на страницах всей этой книги.

Подведем итог. Основные, принципиально неустранимые источники шума в ФПУ, как и во многих других радиотехнических устройствах и полупро­водниковых приборах,— дробовой, генерационно-рекомбинационный, тепловой.

Дробовой шум возникает в приборах с р-п-переходом, а генерационно-реком­бинационный в однородном полупроводнике (в ФР) вследствие дискрет - ности носителей заряда. Носитель, войдя в ОПЗ ФД, а также пара, генери­рованная в ФР, создают приращение тока во внешней цепи. Длительность этого приращения (импульса) определяется соответственно временем проле­та через ОПЗ, временем жизни в полупроводнике. К тепловому току в со­противлениях приводит тепловое движение подвижных носителей заряда: смещаясь, они создают локальное поле и ЭДС, которая потом релаксирует с постоянной времени максвелловской релаксации. При прохождении через электрические цели указанные импульсы могут затягиваться. Так в системе возникают случайные импульсы длительностью тш, определяемой характери­стической постоянной времени этой системы. Хаотическое наложение этих хаотических импульсов и есть шум. Во временной форме шум описывается функцией корреляции, которую можно трактовать как среднестатистический импульс: ее амплитуда К(0) есть дисперсия амплитуды шумового импуль­са, а ее характеристическая постоянная времени ткор —длительность этого импульса тш. Постоянная *т кор-—Тщ определяет временной интервал, на кото­ром две соседние выборки шума коррелированы. Спектр среднестатистичес­кого импульса — функции К{М)—и есть спектр шума (спектральная плот­ность мощности шума) которая является основной характеристикой

•ЭО __

Шума в радиотехнических устройствах. Площадь спектра Г Л (/}й/определяет

И

Дисперсию — средний квадрат значения шума в любой момент времени. В подавляющем большинстве случаев шум подчиняется нормальному закону, так что с помощью этого закона по известной дисперсии можно рассчитать вероятность появления любого значения флуктуирующей величины.