Фотоприемные устройства и ПЗС. Обнаружение слабых оптических сигналов
ОПТИМАЛЬНЫЙ ФИЛЬТР (АНАЛИЗ ВО ВРЕМЕННОЙ ФОРМЕ)
Анализ переходных процессов в линейных системах можно проводить не только в частотной» но и непосредственно ВО Временной форме. В этом случае входной сигнал задается как функция времени: для ФПУ /с (0 = 5Еса*с (0 (сигнал не надо раскладывать на гармоники). Шум также описывается функцией времени — функцией корреляции К{М) (в § 2.2 функция интерпретирована как среднестатистический шумовой импульс), Для усилителя вместо частотной вводят импульсную характеристику Н (Ы) либо переходную. Функцией ЁсаМО’ ^(Д/) и Н(М) достаточно, чтобы рассчитать форму выходного сигнала и функцию корреляции выходного шума, а с их помощью отношение амплитуды сигнала к среднеквадратичному значению шума на выходе усилителя #с/ш и максимизировать это отношение. В общем случае такой расчет громоздок, поэтому до сих Пор мы все-таки применяли частотный метод. Однако анализ во временной форме значительно упрощается, если воспользоваться приближенной методикой — рассматривать последовательность выборок сигнала и шума, а шум аппроксимировать последовательностью импульсов случайной амплитуды со средней длительностью тш. Этого будет достаточно» чтобы вывести все основные закономерности, которые уже были получены частотным методом в § 3.2 и 3.3, найти правило выбора оптимального фильтра, достижимые значения отношения Л^ш и его зависимость от длительности сигнала при различном характере шума. Прагматичный читатель может настоящий параграф пропустить — принципиально новых формул он не найдет. Но анализ во временной форме дополняет и еще полнее раскрывает физическую сущность оптимальной фильтрации, понятней становится обработка сигнала в матричных ФПУ с накоплением с точки зрения оптимальной фильтрации (см. § 4.5 и 4.6). Экономней получаются и некоторые методики расчета например формы выходного сигнала (§ 3.6).
Прежде всего напомним определение импульсной характеристики линейного преобразователя и ее связь с частотной характеристикой коэффициента передачи, подчеркнем аналогию методов анализа в частотной и временной форме.
Прохождение сигнала через фильтр-усилитель. Для описа - ния инерционных свойств линейного преобразователя используют три простых входных тест-сигнала: гармонический, дельтаимпульс, ступенчатый импульс. Реакция на каждый из этих тест-сигналов и определяет соответственно частотную, импульсную и переходную характеристики преобразователя. Зная любую из этих характеристик, легко рассчитать отклик линейного преобразователя на входной сигнал произвольной формы. Методика расчета единая. Надо разложить входной сигнал на
Простых тест-сигналов, найти реакцию преобразователя каждый из них, а она определяется частотной, импульсной либо переходной характеристиками. Складывая эти реакции, олучаем отклик на выходе преобразователя. Именно так подпали при частотном методе анализа (фурье-анализе), где в ячестве тест-сигнала используется гармоника. Рассмотрим те - еоь по аналогии метод импульсных характеристик (переход - Пые характеристики не рассматриваются, так как импульсные дают более наглядное представление об оптимальной фильтр а-
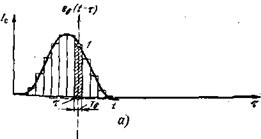
ПШразлшсение выходного сигнала на дельта-импульсы. Чтобы представить себе, как из суммы гармоник восстанавливается сигнал произвольной формы, нужна изрядная доля воображения. А разложение на дельта-импульсы куда наглядней. Сигнал' как бы составляется из последовательности коротких прямоугольных импульсов длительности Га«Тс (рис. 3.14, а). Выделим один такой прямоугольный элементарный импульс /а (заштрихованная область):
И (*—-т) =5£с(т) еь{1— г) — /с(т)£$(/—т) =
= 1сЬ)Тй{ейу—т)/Ге), (3.132)
Б(/_т) =Нш (е0у—т)1Т6), (3.133)
Тде ей{(—т) —относительная форма элементарного прямоугольного импульса; т — временное положение центра импульса. Устремив 0, получим из такого прямоугольного элементарного импульса еь(Т6 дельта-импульс (см. определение в § 2.3), амплитуда которого бесконечна в точке / = т, площадь равна - единице (е6/Т6)Т6 = 1. Графическое разложение сигнала на элементарные прямоугольники (рис. 3.14, а) адекватно следующей аналитической записи:
■* л
Оо
= $ /с(*ж* — 1)с1х. (3.134)
Переход от суммы к интегралу проведен в пределе бесконечно малой длительности элементарных прямоугольных тест-сигналов Т(г+(1х. В фурье-анализе сигнал раскладывается на гармоники различных частот /, а здесь аналогом частоты выступает положение дельта-импульса на оси времени т. Аналогом спектральной плотности /с (0 = ££с ([) является само значение вход - °го сигнала в момент т, /с (т) =5£,с(т), характеризующее интенсивность дельтаобразного сигнала.
Импульсная характеристика. Передаточная характеристика (по определению) есть реакция системы на входной тест-сигнал
|
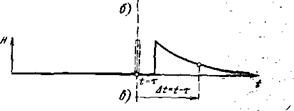
Рис. 3.14. Разложение входного сигнала на дельтаобразные импульсы (а); отклик на каждый из этих импульсов на выходе усилителя повторяет по форме импульсную характеристику усилителя (б, е) |
|
Л^л |
![]() Единичной интенсивности. Подавая на вход усилителя дельта - образный тест-сигнал — импульс тока 1Ь{1—т), получаем выходную реакцию——т). Далее следует отнести эту реакцию к интенсивности входного сигнала. И тут возникает вопрос: в каких единицах измерять его интенсивность? Казалось бы, здесь не должно быть никаких проблем: раз входной
Единичной интенсивности. Подавая на вход усилителя дельта - образный тест-сигнал — импульс тока 1Ь{1—т), получаем выходную реакцию——т). Далее следует отнести эту реакцию к интенсивности входного сигнала. И тут возникает вопрос: в каких единицах измерять его интенсивность? Казалось бы, здесь не должно быть никаких проблем: раз входной
Сигнал — ток, то его интенсивность необходимо измерять в амперах. Именно так поступали в фурье-анализе при расчете коэффициента передачи усилителя К21 (/): относили амплитуду выходного напряжения (В) к амплитуде входного тока (А), получая размерность /С21 (/) в омах (напомним, что речь идет об усилителе-преобразователе тока в напряжение). Однако мерой интенсивности дельтаобразного тест-воздействия является не амплитуда, а его площадь. В самом определении дельта-импульса в качестве его меры выступает площадь (она единична). Интенсивность импульса 1й{1—%) по (3.132) также характеризуется площадью — зарядом /с(т)Гб. Выходная реакция системы Оъ(£—т) оказывается пропорциональной не амплитуде, а площади дельтаобразного входного сигнала. И это нетрудно доказать.
Подадим на вход системы п дельтаобразных элементарных импульсов МО, произвольно наложив их друг на друга — лишь бы все они укладывались на очень малом отрезке времени И форма, и амплитуда такого сложного
Входного импульса будут произвольными, задана только его площадь (заряд). Она в п раз больше площади (заряда) каждого элементарного импульса. По определению длительность дельта - образного импульса Ть> и поэтому пТ6 меньше всех характеристических времен системы, в том числе и времени релаксации выходного сигнала —т). Следовательно, с точки зрения усилителя все эти элементарные импульсы приходят как бы в один момент времени Реакции на каждый элемен
Тарный импульс £/#(*—т) оказываются синхронными, они дружно складываются, и выходное напряжение возрастает в те эке п раз, что и площадь входного импульса. Что и требовалось доказать.
Определим импульсную характеристику системы Н(I—т)* отнеся выходную реакцию к площади входного дельтаобразно - го импульса /с(т)Га:
Я(*-т)~Г/в(*—т)//с(т)Гв. (3.135)
Сопоставив это определение с определением коэффициента передачи К23 (?) ~£МШМП» видим, что их размерности различаются — в размерности Н появилась «лишняя секунда»:
Размерность Я —[размерность /С2]]/секунда = Ом/с = 1/Ф.
Если на вход системы подан дельта-импульс, то выходной сигнал непосредственно является импульсной характеристикой. Полагая в (3.129) — (3.132) площадь /с(т)Тв=1, получаем
1,(0 - б (*—т); Я (*—т) эз ий (/—т). (3.136)
Но можно ли считать площадь токового импульса равной единице (безразмерной величины), если эта площадь представляет собой заряд (Кл)? Можно, но только при переходе к безразмерным величинам, когда /б) Т6, и& обозначают не собственно физическую величину, а ее численное значение в выбранных единицах измерения, например (А), (с), (В). В дальнейшем выражении типа (3.133) встретятся, но специально оговаривать безразмерность величин больше не будем.
И завершим настоящий раздел, примером импульсной характеристики (рис. 3.14, б, в). Эта характеристика зависит от интервала времени —% между моментами опроса ( и прихода т входного дельта-импульса. На рис. 3.14,6 в качестве переменной выбрано время т, а на рис. 3.14, в — время I. Ясно, что построенные на этих рисунках функции зеркальны, поскольку переменные т и / входят в функцию Н(1—т) с разными знаками. Функция Н(т) понадобится в дальнейшем при расчете выходного сигнала в фиксированный момент времени ti когдз на вход приходят дельтаобразные импульсы в различные мо-
Тленты т. А функцию текущего времени обычно
Получают экспериментально, подавая на вход дельта-импульс в некоторый момент т.
В общем случае усилитель искажает сигнал. На примере рис. 3.14,5 затягивается спад, вносится задержка (максимум отклика сдвинут относительно момента прихода входного сигнала т). В фурье-анализе этим двум искажениям можно поставить в соответствие амплитудно- и фазочастотные искажения.
Связь импульсной и частотной характеристик легко1 прослеживается на следующем опыте. Подадим на вход фильтра-усилителя дельта-импульс — на выходе получим импульсную характеристику Я(*—т) = £/*(*—т) (рис. 3.15). Спектр дельта - импульса белый, поэтому с точки зрения фурье-анализа на вход поданы гармоники всех частот / одинаковой амплитуды, каждая из этих гармоник усиливается в Ku{f) раз, так что на выходе получаем спектр гармоник K2{f). Итак, с выхода усилителя снимаем сигнал U6(t—т)=H(t—т), а на языке фурье-анализа — это спектр /С21 (f) - Так доказывается известное положение теории линейных систем: частотная характеристика такой системы Knif) является спектром ее импульсной характеристики H(t—т). Отсюда следует, что если частотная характеристика известна, то импульсная рассчитывается с помощью обратного фурье-преобразования:
Оо
И (ДО =5 (/) К21 (/) cos (соДt + яру) df=
О -
|
(3.137) |
![]() 2 5 К-а (/) COS (ыМ 4-^)у) df.
2 5 К-а (/) COS (ыМ 4-^)у) df.
|
/ |
![]() Фильтрующие свойства усилителя характеризуются не абсолютными, а относительными характеристиками передачи. Логично определить относительные характеристики (импульсную и частотную) применительно к одному и тому же усилителю.
Фильтрующие свойства усилителя характеризуются не абсолютными, а относительными характеристиками передачи. Логично определить относительные характеристики (импульсную и частотную) применительно к одному и тому же усилителю.
|
Dft-r) JL*-t |
О-- |
H(t |
|||
|
T |
ОД |
И |
|||
|
И |
1' |
1 |
- I, |
||
|
^5* |
|
Ев |
|
У |
|
T-ri |
|
Рис. 3.15, Частотная характеристика усилителя—это спектр его импульсной Характеристики |
Его коэффициент усиления (передачи) в Ко раз меньше, чем в реальном, т. е. в области плато частотной характеристики он равен единице. Для такого усилителя
К(1)=К21(П1*<0, Н(М)=Н{М)1Ко. (3.138)
Согласно этому определению и (3.135) характеристика Н(М) остается размерной — ее размерность с-1. Из (3.137) и
(3.138) вытекает следующая связь между относительными характеристиками.
Оо
А'(Д0 = 2 (/)с°8(й>Л#-Ьфу)^/. ' / (3.139)
О
Форма выходного сигнала. Итак, выходной сигнал /с (т) разложен на дельтаобразные импульсы /а (т) =/слес(т)б (/—т) и определены отклики на каждый такой импульс 0й (7—г) ~ ~Н(7—т). Они одинаковы по форме и различаются лишь амплитудой и положением во времени (поскольку различны площади и моменты прихода входных дельтаобразных импульсов). Теперь остается сложить все эти отклики и получить искомый сигнал на выходе усилителя
Со
= § /с(т)//(<-т)^т, (3.140)
—оо '■
{ ... . /
^ — х)йх ис{£)= ^ ес(т)А(* — т)(3.141)
— оо —сс
Здесь использовано определение импульсной характеристики (3.135), переход от суммы к интегралу проведен в пределе Ть^с1 т-*0.
Полученный интеграл свертки (3.140), (3.141) заменяет
При анализе во временной форме обратное фурье-преобразование и позволяет ПО известным входному сигналу /с (т) =5£'сА^с (т) и импульсной характеристике Я(Д£) найти выходной сигнал. Применяют обе приведенные формы записи интеграла свертки. Физически реализуемая система не может реагировать на входное воздействие, которого еще нет, поэтому в такой системе при т>(, Л£<0. В этом случае в (3.140) верхний предел (бесконечность) изменяется на значение t, и автоматически приходим к (3.141). Она представлена как для абсолютных ис, /с, Я, так и относительных ис, ес, к величин.
Приведенных сведений об импульсной характеристике достаточно для дальнейшего анализа. Прежде всего попытаемся найти импульсную характеристику оптимального фильтра, используя знания о его частотной характеристике.
Импульсная характеристика оптимального фильтра при белом шуме повторяет форму сигнала. Анализ начнем с белого шума и сигнала симметричной формы. Частотная характеристик ка оптимального фильтра k (/) является не только спектром импульсной характеристики h(At), но одновременно и спектром сигнала ez(t) (см. § 3.2). А раз спектры функций h(А/) и ec(?) совпадают, то совпадают (по форме) и сами эти функции:
H(At) =Bec(t-t^)=ez(At-t3aa)jTCi (3.142)
Где В = const.
Как видим, константа пропорциональности выбрана здесь равной эффективной длительности сигнала. Иной она и не может быть. Спектральная плотность h(At) на нулевой частоте есть k(f)=k(0)=1. А в § 2.1 было показано, что она должна быть равна площади импульса — в данном случае импульса h(At), и лишь при указанном значении константы это требование будет соблюдаться:
00 со
^ H (t)dt = ес(Ы — t3B!,)dt =^7’с=1. (3.143)
—со О
В (3.142) и (3.143) фигурирует время задержки? зад, которое (см. § 3.2) произвольно и не влияет на отношение сигнал-шум,, определяет только момент, когда это отношение достигает максимума.
Получили еще одно замечательное свойство оптимального фильтра: форма его импульсной характеристи
Ки в точности повторяет форму входного сигнала, на который настроен этот фильтр, — точно так же, как частотная характеристика фильтра повторяет спектр сигнала.
Этот вывод сохраняется и при асимметричной форме входного сигнала, но с одним уточнением. Поскольку частотная характеристика фильтра комплексно сопряжена со спектром сигнала x(f) = ес* (f) (см. § 3.2), то импульсная характеристика является зеркальным отражением входного сигнала:
H(At)=ec(—At-Ua! l)/Tc. (3.144)
К сожалению, этот «красивый» результат справедлив только при белом шуме, так как при произвольном спектре шума частотная характеристика оптимального фильтра уже отличается от спектра сигнала и K(f) =ес* (f)jQ(f). Подставляя эту характеристику в (3.137), получаем
Оо
H (ДО = 2 ^ k (/) cos (а>Дt — t|)c) df =
О
ОО
= 2 jj!^c°s(c^_^c) df. (3.145)
При ВЧ-шуме спад подынтегральной функции начинается на низких частотах fв<Cfc, где спектральная плотность сигнала ■еще постоянна, ес(?) = 1, ^(О^О - Поэтому импульсная характеристика не зависит от спектра сигнала.
Оо
|
Й(Д<)»2 |
![]() Т+ЦШ 005 аШ/“2^ЄХР ("1 At 1/Та)'
Т+ЦШ 005 аШ/“2^ЄХР ("1 At 1/Та)'
|
|
При вычислении (3.146) использованы таблицы интегралов |79]. Низкочастотный спад обусловливает и большую эф
Фективную постоянную времени фильтра тв-
|
Оо |
![]() Теперь остается получить импульсную характеристику оптимального фильтра при НЧ-шуме. Форму входного сигнала принимаем колоколообразной, так как постановка задачи оптимизации при прямоугольном сигнале и НЧ-шуме некорректна (см. § 3.3). Постараемся угадать форму импульсной характеристики А(Д?)- Чем, собственно говоря, отличается наш фильтр от рассмотренного оптимального фильтра при белом шуме? Частотная характеристика и того и другого фильтра повторяет ■спектр сигнала — в данном случае косинусквадратного, только при НЧ-шуме усиление фильтра на низких частотах падает ■обратно пропорционально ©(/). Утрируя, можно сказать, что этот фильтр отличается только тем, что не пропускает постоянную составляющую (и очень низкочастотные гармоники, когда /н<С1/2Гс). Но если совладают частотные характеристики фильтров к:(И, то должны совпадать и их импульсные характеристики к (А/). Форму характеристики к{Ы) при белом шуме. знаем — это форма колоколообразного сигнала. Следовательно, импульсная характеристика Л(Д/) оптимального фильтра при НЧ-шуме есть тот же входной колоколообразный сигнал. А как отражается на импульсной характеристике фильтра Л(Д/)~ '"'^(Д/) его особенность — то, что он не пропускает постоянную составляющую? На языке формулы (3.141) это выражается так: при постоянном входном сигнале ес{1) = 1 на выходе Должны получить мс = 0:
Теперь остается получить импульсную характеристику оптимального фильтра при НЧ-шуме. Форму входного сигнала принимаем колоколообразной, так как постановка задачи оптимизации при прямоугольном сигнале и НЧ-шуме некорректна (см. § 3.3). Постараемся угадать форму импульсной характеристики А(Д?)- Чем, собственно говоря, отличается наш фильтр от рассмотренного оптимального фильтра при белом шуме? Частотная характеристика и того и другого фильтра повторяет ■спектр сигнала — в данном случае косинусквадратного, только при НЧ-шуме усиление фильтра на низких частотах падает ■обратно пропорционально ©(/). Утрируя, можно сказать, что этот фильтр отличается только тем, что не пропускает постоянную составляющую (и очень низкочастотные гармоники, когда /н<С1/2Гс). Но если совладают частотные характеристики фильтров к:(И, то должны совпадать и их импульсные характеристики к (А/). Форму характеристики к{Ы) при белом шуме. знаем — это форма колоколообразного сигнала. Следовательно, импульсная характеристика Л(Д/) оптимального фильтра при НЧ-шуме есть тот же входной колоколообразный сигнал. А как отражается на импульсной характеристике фильтра Л(Д/)~ '"'^(Д/) его особенность — то, что он не пропускает постоянную составляющую? На языке формулы (3.141) это выражается так: при постоянном входном сигнале ес{1) = 1 на выходе Должны получить мс = 0:
Оо
|
(3.147) |
![]() (/)= jj ес(т) h (^т) dt= ^k{t~~i)dx=0.
(/)= jj ес(т) h (^т) dt= ^k{t~~i)dx=0.
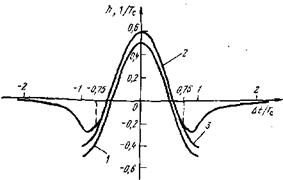
Следовательно, кривую h(t—x)~ec(t—т) надо сместить вниз таким образом, чтобы площадь под этой кривой стала равна нУлю, Так пришли к импульсной характеристике оптимального фильтра (кривая 1 на рис. 3.16). Здесь площадь под кривой
H[&t) приравнена нулю условно на интервале [—Тс, Тс].
|
Рис. 3.16. Импульсная характеристика при НЧ-шуме смещается вниз {относительно этой характеристики при белом шуме), и в ней появляются отрицательные выбросы |
Угадали или нет? Подставляя в (3.141) спектр шума 0 (0 =/н//=*н/* и сигнала Јc(f)=n2 sinлг/j:(іг3—хг), x=2jxfTc^
Хн~2л[нТс, получаем
ОС
H (Дt) = 2 jj ес cos (2я/Д0<^/ =
О
СО
П С я2 sin х і At х, --
/ 2д2 Р sin х [At .
= [ЪЯГ7) J 1ІПГЇГ COS
(3.148>
Напомним, что при НЧ-шуме коэффициент усиления (и, следовательно, ^(ДО) нормируется дополнительно на значение ^с//н = [1/2^нТ’с] (3.65). При такой нормировке
Оо
|
(3.149) |
![]() A(A<)=T7S^=IrCosf^JC)rfJi:-
A(A<)=T7S^=IrCosf^JC)rfJi:-
Импульсная характеристика по (3.149) также построена на рис. 3.16, кривая 2. Численный расчет подтверждает угаданное поведение характеристики Л(Д/): она совпадает по форме с ко - синус-квадратным импульсом сигнала ес(і). Правда, смещение вниз оказывается несколько меньше (ср. кривые }~3)г
И указанное совпадение наблюдается не при всех временах (но все же на весьма широком интервале 1Лг|<0,75Тс порядка времени действия сигнала). При больших временах (|Д/|>‘ *>0 75Гс) характеристика медленно релаксирует к нулю. Такое поведение не было предсказано, и понятно почему: большим
Временам соответствуют низкие частоты, а именно на низких частотах в большей степени мы отклонились от реальной зависимости к{!) =ес(/)/©(/), когда при качественном построении
Полагали, что к(/)^£с(/Ь
Принципиальное отличие полученной импульсной характеристики от рассмотренных — это наличие в ней отрицательных выбросов. Следовательно, входные воздействия на соответствующих интервалах суммируются с отрицательным весом. Фильтр осуществляет не только арифметическое сложение, но я вычитание.
Еще раз о правиле принятия решения о наличии или отсутствии сигнала. Рассматривая в § 3.1 это правило, мы обошли молчанием вопрос; почему это решение принимается решающим устройством только по одной выборке, хотя бы и в момент достижения сигналом своего максимума? Казалось бы, такой алгоритм неоптимален, не используется остальная информация, содержащаяся во входном сигнале, который отличен от нуля на достаточно большом отрезке времени (около (I. ..2)7^). Из общих соображений выбираем следующий алгоритм для решающего устройства: брать выборки на всем интервале действия сигнала Uc. it), составлять по определенному правилу их суперпозицию и принимать решение уже с помощью этой суперпозиции. Тогда действительно будет полностью использована информация о сигнале (вся его мощность) .
Временная форма — интеграл свертки (3.141) показывает, что нет нужды выполнять такой алгоритм в решающем устройстве, так как необходимую операцию суперпозиции выборок сигнала выполняет сам оптимальный фильтр. Он складывает все выборки со взвешенным коэффициентом /г(Дт). Вот почему решающему устройству достаточно сравнивать максимальное значение выходного сигнала с некоторым пороговым уровнем (см. § 3.1).
При анализе во временной форме задача оптимальной фильтрации сводится к оптимизации взвешенного коэффициента — импульсной характеристики Н(Ах)—таким образом, чтобы Из смеси сигнала с шумом выбрать «побольше» сигнала и «поменьше» шума. Выполним эту оптимизацию последователь - Но для хорошо известного нам набора шумов (белого, высокочастотного и низкочастотного).
Белый шум. Пусть на вход приходит сигнал прямоугольной Формы (рис. 3.17,а). Для белого шума используем аппроксимацию (см. § 2.2) в виде последовательности импульсов случай -
Выброса), поэтому при сложении этих выборок в одинаковое число раз увеличивается и сигнал /аН-^сп = 25£са> н шум
*ш1-ИшП=2*ш; + = /(2^)2 =2■ так Что
Отношение сигнал-шум, к сожалению, не улучшается. все-таки
На практике следует устанавливать очень малый интервал между выборками, много меньше времени Хотя отношение
Л^с? ш не улучшается, но мы освободимся от условности модели. При столь частых выборках их надо не синхронизировать с шумовыми выбросами (это можно нарисовать на рис. <5Л7,в, г, но нельзя осуществить на практике), а автоматически усреднять по шумовым импульсам разной длительности и наложенным друг на друга.
|
2 П 2 *=і |
![]() Каково правило суперпозиции выборок при сигнале произвольной формы £с(0? Сложим при таком сигнале выборки с весом А*. Тогда (3.151) — (3.154) модифицируются:
Каково правило суперпозиции выборок при сигнале произвольной формы £с(0? Сложим при таком сигнале выборки с весом А*. Тогда (3.151) — (3.154) модифицируются:
^к^ск— ’“Г ■ 1 (3.156)
'Т'4 ” V - ■ ". •
(3,157)
2 4л = 4(Аі+А2+...А«)
*=1
= 2?/„,(Аі+АІ+...а5)/2тш; (3.158)
Л'с/ш=-4=-У2т^г - (3.159)
' У2 Ма»! +*»» + ••• + ЛЛ
Точно такая же дробь (последний множитель правой части) была получена при анализе соотношения Ач/’ш в частотной форме (3.43), только там вместо кп, есп фигурировали кл, еСп(їп). По аналогии с (3.43) следует, что максимум рассматриваемой дроби достигается при Ьк = ек, т. е. при /г(АО ~ес(Л0* Еще раз доказали, что импульсная характеристика оптимального фильтра при белом шуме повторяет форму обнаруживаемого сигнала, но доказали уже «честно», совсем не пользуясь результатами частотного анализа, вовсе не привлекая частотную характеристику фильтра.
Высокочастотный шум. ВЧ-сосгавляющая шума появляется при емкостном входном импедансе (рис. 3.17,ж), когда генератор ЭДС шума замещается генератором шумового тока, подключенным параллельно фотоприемнику (см. § 2.4). Теперь будем непосредственно оперировать схемой на рис. 3,17,^- Реализацию ЭДС-шума £/ш(0» как и токового шума, аппроксимируем последовательностью прямоугольных импульсов
(рис. 3.17, По аналогии с (3.150) среднеквадратичное значение (выборки в любой момент времени) связано
Со спектральной ПЛОТНОСТЬЮ (/) соотношением
£/^2/2тш. (3.160)
Как видно из рис. 3.17, ас, ток сигнала /с накапливается на входной емкости и создает постоянное напряжение Uc = IcTcfCsx (рис. 3.17, д). Именно процессу накопления на емкости обязаны тем, что выходной сигнал и его отношение к шуму зависит от площади (энергии) входного сигнала ЕсаТс Конкретная форма сигнала никак не влияет на результат накопления. Об этих особенностях также говорилось при частотном анализе и отмечалось, что при бесконечно длинном импульсе отношение JV A стремится к бесконечности (см. § 3.3). На язык формул сказанное переводится следующим образом:
U^nSEoJJC^. - (3.161)
Uш ~ Uт - f - £/Ш2 - f - ... + f/щ п< (3*162)
Ьi^nЬl, = n? ml 2тш, . (3.163)
ЛГС/Ш= uJVUl= VnSE, ATJC, x
= SE ch T c V2xmпijCBXem, (3.164)
Lim Ncim-+ со. (3.165)
Tl-*- oo
Опять повторение результата § 3.3: при наличии только ВЧ - шума полоса усилителя должна выбираться бесконечно узкой (следовательно, время наблюдения бесконечно большим 1/2/у), тогда обеспечивается бесконечно большое значение ^с/шоф. В § 3.3 было также показано, что реально значение ^с/щоф ограничивается белой составляющей шумов, так что учтем ее теперь и в схеме рис. 3.17, ж. Рассмотрим вновь реализацию 1щ(0 (рис. 3.17,6). Шумовые импульсы imK накапливаются на входной емкости СВх точно так же, как и сигнальный импульс, создавая на входе усилителя после своего прихода случайный скачок напряжения 1пшТш/Свх. Это напряжение опрашивается при каждой последующей выборке. Поскольку оптимальный фильтр, настроенный на прямоугольный сигнальный импульс, суммирует все выборки за время Гн, то первый шумо - Е°й импульс (нумерация на рис. 3.17,6) к моменту отсчета Та °просится и просуммируется п раз, второй импульс п—1 раз и
Последний — только один раз. Поэтому при опросе к концу ин, тервала наблюдения сумма выборок напряжений будет равна
(п—1) /Свх+
“Ь*1шТш(я. 2)/Свх+ ■ • • Ч-^шпТш/Свх. (3.166)
А дисперсия этой суммы п независимых слагаемых определится выражением
{Ж=гшт»[гег + (гс~ 1)г + (я-2)г+ .. .2з + 1Гу с2п. (3.167)
Оценим ряд в правой части полученного уравнения. Если бы все п слагаемых были одинаковыми и равными п2, то сумма ряда составляла бы пг. Первые члены ряда мало отличаются от м2. Они самые большие и определяют значения всей суммы, поэтому можно ожидать, что сумма по своему порядку приближается к значению п3 (оставаясь меньше). Из таблиц рядов [79] следует, что сумма рассматриваемого ряда равна пэ/3. И (3.167) с учетом (3.150) преобразуется к виду
£/ш = Свх - 3 = 2д1шх2шп?/2^шС2м-3 =
= 2д1штшпэ/С1,-2-3. (3.168)
В результате двойного накопления на входной емкости и в самом оптимальном фильтре компонента мощности токового шума возрастает с ростом времени наблюдения значительно сильнее /г3~7’н3> чем компонента мощности электродвижущей силы шума (п~Тп формула (3.163)). При некотором значении п=т обе компоненты сравниваются
2 <7/штшю3/Свх* 2- 3 = е2щт(2хш> Тщ т2 = е2тс1к -3/2д/ш,
= УдетС9Л1У2яй = >аЗ/2я/в. (3.169)
В (3.169) использовали определения частоты [в (2.139). (Учет дробового шума привел к тому, что время наблюдения стало конечным, но все равно оно значительно превышает длительность сигнала Тс. Это следует из (3.169), если учесть, что рассматривается случай, когда ВЧ-шумы преобладают в диапазоне частот сигнала:
/.«/*= 1/27'с; Т„-(/3/л2/„»7'с. (3.170)
Полученные значения т и 7’н являются оптимальными. При меньшем числе выборок (/г<т) преобладает ЭДС шум, а при таком шуме для повышения отношения Мс/Ш следует увеличивать число выборок (3.164). Но как только число выборок пре - высит значение т (3.169)’ отношение сигнал-шум начнет падать, поскольку здесь преобладает белый шум и при накапливается только дополнительный шум.
Определив оптимальное время Тн, легко рассчитать и отно-
Шение сигнал-шум. Для сигнала воспользуемся формулой
(3.138) . Для определения дисперсии шума используем формулу мощности дробового шума (3.165), но только удвоим эту мощность, поскольку при выбранном времени Тп и дробовой, И ЭДС-шум дают равный вклад в общий шум. Подставляя в эти формулы значение Тн^тхш из (3.169), получаем ц 5£сАт/Свх
Д/-°Ф_ . ____ — —
™ с/ш — 77Т
2 (2^/ш) -гштэ/бС
SHAPE \* MERGEFORMAT ![]()
|
2я/в |
![]() 5£_сА^ т/ 3 Г~Ъ~
5£_сА^ т/ 3 Г~Ъ~
2,
|
У 2?/ |
![]() ^ > %т У2?/ш I/ УЗ
^ > %т У2?/ш I/ УЗ
Т
V 2<7/ш
Сравним этот результат с точным выражением (3.77), полученным частотным методом. В (3.171) появился «лишний» множитель > 3=1,31, так что ошибка составляет всего 31%. А ведь были сделаны серьезные упрощения и в части модели шумов (представляли его последовательностью прямоугольных импульсов длительностью тш), и в части обработки сигнала (складывали выборки на интервале Гн без веса Л(А£)).
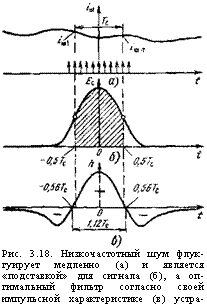
Низкочастотный шум. В этом случае сам источник шумов отличается от рассмотренных до сих пор (дробового, теплового): в его спектре преобладают низкочастотные гармоники, поэтому и шумовая реализация 1ш(0 является медленно изменяющейся случайной функцией. Во всяком случае, ее изменения малы за период действия сигнала Тс (рис. 3.18, а, б). Все выборки шума в течение действия сигнала Тс оказываются почти ПОЛНОСТЬЮ коррелированными, Гцн^ша'» а мы
Видели, что при сложении таких выборок шум растет точно так же, как сигнал:
0с=п5Еса, (3.172)
Иш = п1ш, и1 = ПЧгш. ' (3.173
Поэтому их отношение
N1^= п!!1± - = (3.174)
У пч2ш У 4
Не зависит от числа выборок и, следовательно, от длительности импульса Тс. Так физически объясняется одна из важных особенностей оптимальной фильтрации импульсного сигнала на фоне НЧ-шума.
Сложность дальнейшего расчета заключается в том, что теоретически дисперсия НЧ-шума стремится к бесконечности:
Как избежать этой расходимости? Еще раз обратимся * рис. 3.18. Реализацию шума £ш(0 можно рассматривать как случайную величину, почти постоянную в течение времени действия сигнала — его эффективной длительности Тс - Очевидно, что из смеси сигнала с шумовой «подставкой», выбранной на интервале [—0,5 Тс, 0,5 7С], надо вычесть эту «подставку». Последнюю надо измерять, когда сигнала нет или почти нет при —0,5 Тс, />0,5 Тс’ И оптимальный фильтр выполняет именно эти необходимые операции, что следует из его импульсной характеристики, которая усердно перенесена на рис. 3.18,5 с рис. 3.16: этот фильтр складывает выборки с положительным весом на интервале [ — 0,56 Гс, 0,56 Гс] и с отрицательным— вне этого интервала. __
|
Рис. 3.18. Низкочастотный шум флуктуирует медленно (а) и является «подставкой» для сигнала (б), а оптимальный фильтр согласно своей импульсной характеристике (в) устраняет эту «подставку» |
 Для дальнейшего расчета — определения дисперсии 1Ш2 —- надо знать функцию корреляции. К сожалению, ее расчет достаточно громоздок. Когда будем анализировать матричные ФПУ с накоплением и вычитанием кадров (см. § 4.5) —операциях, идентичных только что рассмотренным, вернемся к определению /щ* И отношения А'суш - При этом также будут получены формулы для ЫС/ш, подобные формулам для оптимального фильтра (§ 3.3).
Для дальнейшего расчета — определения дисперсии 1Ш2 —- надо знать функцию корреляции. К сожалению, ее расчет достаточно громоздок. Когда будем анализировать матричные ФПУ с накоплением и вычитанием кадров (см. § 4.5) —операциях, идентичных только что рассмотренным, вернемся к определению /щ* И отношения А'суш - При этом также будут получены формулы для ЫС/ш, подобные формулам для оптимального фильтра (§ 3.3).
|
А |
-г/г* |
|
|
1 |
||
|
Ь |
|
|
^_____________ _ |
|
Рис. 3.19. Импульсные характеристики свидетельствуют: оптимальный Фильтр является накопителем (а) или эквивалентен накопителю (б, в), а при НЧ-шуме — накопителем втройне (г) |
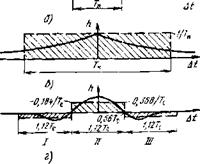
Оптимальный фильтр-накопитель как элемент памяти. Анализ во временной форме позволяет глубже раскрыть сущность процесса оптимальной фильтрации. Из правила «Импульсная характеристика оптимального фильтра повторяет форму сигнала» вытекает, что в классическом случае белых шумов и прямоугольной формы сигнала импульсная характеристика тоже прямоугольна (рис. 3.19, а). Фильтр с такой импульсной характеристикой можно интерпретировать как элемент памяти: короткое входное б-воздействие вызывает на выходе постоянный отклик длительности Тв, т. е. в течение Ти фильтр как бы помнит об этом воздействии. Время Гн можно назвать глубиной памяти. Оптический сигнал прямоугольной формы состоит из суммы элементарных б-воздействий на интервале Тс. Глубина памяти оптимального фильтра выбрана в точности такой, чтобы запомнить все эти воздействия, Тц=Тс. Все запоминаемые на интервале Тп выборки складываются, так что время Т„ — это и время наблюдения, в течение которого берутся выборки, и глубина памяти, и интервал интегрирования, накопления, сложения. То, что оптимальный фильтр интегрирует (накапливает) сигнал, следует и из интеграла свертки (3.141) при подстановке в него прямоугольной импульсной характеристики:
Г I
Ис= 5 * 6с ^ (3.176)
*~ГН
В накоплении на интервале ТН=ТС — суть, железная логика оптимальной фильтрации: именно при таком времени накопления (глубине памяти) полностью используется информация о входном сигнале и не накапливается (не запоминается) лишний шум.
Оптимальный фильтр можно рассматривать и как накопитель при произвольной форме сигнала. Только он накапливает (суммирует) входные воздействия с весом к, и можно говорить о некотором эффективном времени накопления Тн: им
Пульсную характеристику произвольной формы Л(Д£) можно заменить на эквивалентный прямоугольный импульс кд(М) так, как это было сделано с сигналом (см. § 2.1). Длительность эквивалентного импульса кь{М), равная площади под кривой /г(ДО, и будет эффективным временем накопления Гн— эффективной глубиной памяти (рис. 3.19,6). Для оценки выходного сигнала импульсную характеристику в интеграле свертки (3.139) можно заменить эквивалентной (прямоугольной) , сводя алгоритм обработки к накоплению:
Ис(0 = ^ к (*— т)£с(т) ^ ес(х)с1т. (3.177)
—°° "г— т..
Поскольку при белом шуме Л (ДО ~ес(Д0> то эффективное время накопления, как и при сигнале прямоугольной формы, равно эффективной длительности сигнала Тн= Тс.
Оптимальный фильтр фактически остается накопителем и при ВЧ-шуме, только эффективное время накопления становится значительно больше длительности сигнала. Именно операцию накопления (сложения выборок) выполнял фильтр при ВЧ-шуме. При оптимизации времени накопления было получено значение ТшгЗ/2л? вч==,7ту^>Тс (ЗЛ69), Строго говоря, в оптимальном фильтре выборки должны складываться с весом к, но, заменяя функцию Л (ДО эквивалентным прямоугольником Лэ(Д0 (рис. 3.19, в), сводим такую обработку к накоплению. Так как фронт и спад импульса Л (ДО экспоненциально релаксируют с постоянной времени тэ (3.147) (рис. 3.19, в), то длительность этого импульса, определяющая и эффективное время накопления, равна
7н=2тэ=2/2я/в=1/я/в. (3.178)
Полученное значение по (3.169) отличается от последнего всего на 15%.
Оптимальный фильтр при НЧ-шуме также выполняет операцию накопления, но не ограничивается этим. Импульсную характеристику (рис. 3.19, г) нельзя заменить одним эквивалентным прямоугольником: поскольку постоянная составляющая не пропускается, то площадь под кривой Л (ДО и, следовательно, интервал Тп равны нулю. Каждый из трех участков характеристики Л (ДО (один положительный I и два отрицательных II, III) следует заменить соответствующими прямоугольниками тех же знаков. Возможны различные варианты подобной эквивалентной замены. Но больше всего должна понравиться читателю аппроксимация Лэ(Д0 (рис. 3.19,г, штриховая линия), потому что она особенно наглядно демонстрирует особенности оптимальной обработки сигнала при НЧ - шуме. Прототипом здесь является стандартный способ обработки при белом шуме: на основном интервале I точно так же проводится накопление сигнала в течение времени, почти равного его длительности. Модификация способа заключается в появлении побочных интервалов II, III - Расположены они непосредственно около основного так, чтобы накапливаемая на этих интервалах шумовая «подставка» не успела сильно измениться. Эффективное время накопления такое же, как и на основном, а значение Лэ(Д0 вдвое меньше. Поэтому сигналы, накопленные от постоянной составляющей на интервалах I, а также П+Ш, равны и при вычитании полностью компенсируют друг друга. Это и есть основная особенность фильтра при НЧ-шуме. Рассмотренной аппроксимации Аа(Л0 соответствует следующая запись интеграла свертки:
![]()
|
_Гоо /-1,687'с <+0,5бГ^ *+1,68Гс |
![]()
![]()
|
*+1,68Г |
![]()
|
(3.179) |
![]() Таким образом, при любом характере шума устройство выполняет накопление (эффективное накопление), обладает памятью. И это неудивительно; память — необходимое свойство разума, а обнаружитель все-таки является «разумным» устройством (хотя бы и самым элементарным) — самостоятельно принимает решение о наличии или отсутствии сигнала. Вообще обнаружитель может запоминать следующую информацию: текущие выборки смеси сигнала с шумом; форму обнаруживаемого сигнала при белом шуме, представленную в частотной (переходной) характеристике:
Таким образом, при любом характере шума устройство выполняет накопление (эффективное накопление), обладает памятью. И это неудивительно; память — необходимое свойство разума, а обнаружитель все-таки является «разумным» устройством (хотя бы и самым элементарным) — самостоятельно принимает решение о наличии или отсутствии сигнала. Вообще обнаружитель может запоминать следующую информацию: текущие выборки смеси сигнала с шумом; форму обнаруживаемого сигнала при белом шуме, представленную в частотной (переходной) характеристике:
КШ)=ес{Ы)/Тс;
Информацию о спектре шума к (/) —ес (/)/© (/), которая присутствует в частотной характеристике при небелом шуме;
Значение порога £/пор. при сравнении с которым выходного отклика и принимается решение — пришел или не пришел сигнал.
Представление об оптимальной фильтрации как процессе накопления (при НЧ-шуме в сочетании с вычитанием) особенно полезно при анализе обработки сигнала в многоэлеМентных ФПУ, ПЗС, ПЗИ. Накопление в этих приборах является оптимальной (почти оптимальной) обработкой сигнала. Впрочем, этот вопрос столь важен, что он специально будет рассмотрен в § 4.5 и 4.6.
Подведем итог. Имупльсная характеристика оптимального фильтра в случае белого шума повторяет форму обнаруживаемого сигнала (при несимметричном импульсном сигнале является его зеркальным отражением). Следовательно, при прямоугольной форме сигнала импульсная характеристика тоже прямоугольна. А это значит, что оптимальный фильтр является накопителем с временем накопления Тп = Тс. Но и в самом общем случае оптимальную обработку можно в первом приближении аппроксимировать операцией интегрирования. При белом шуме эффективное время накопления (интегрирования) Тл остается равным эффективной длительности обнаруживаемого сигнала Тс при любой его форме. В случае ВЧ-шумов время ТЛ много больше длительности сигнала и определяется граничной частотой ВЧ - шума Гн—^я/в. При НЧ-шуме накопленные на соседних временных интервалах сигналы вычитаются, что устраняет медленную низкочастотную флуктуацию шума.
Обнаружитель как логическое устройство (ведь оно принимает решение 0 наличии сигнала и его отсутствия) должно обладать памятью. Накопление
в оптимальном фильтре, позволяющее запомнить всю необходимую теку, Шую информацию о смеси сигнала с шумом, является одним из элементов такой памяти.
Анализ во временной форме позволил вывести уже известные по частотному анализу основные закономерности оптимальной фильтрации: правила выбора фильтра в зависимости от характера шума, формы сигнала, достижимые значения отношения сигнал-шум.