Фотоприемные устройства и ПЗС. Обнаружение сла­бых оптических сигналов

ФОРМА СИГНАЛА НА ВЫХОДЕ ОПТИМАЛЬНОГО ФИЛЬТРА

Достоянием истории стали первые опыты по обнаружению слабых сигналов. Исследователи, пытаясь получить максималь­ный сигнал, выбирали фильтр широкополосным [4] и вопроса о форме выходного сигнала не возникало — она воспроизводи­ла форму входного. При широкой полосе фильтра, конечно, удавалось получить амплитуду сигнала максимальной, но неоправданно завышался шум. Как было показано в § 3.2, по­лоса оптимального фильтра должна быть ограниченной. При белом шуме она совпадает с полосой обнаруживаемого сигна­ла /с, а при ВЧ-шуме значительно уже — определяется гранич­ной частотой этого шума [в-С/с (§ 3,3). Поэтому можно ожи­дать, что оптимальный фильтр затягивает сигнал примерно в 1,5 раза при белом шуме, поскольку в этом случае /с=/у и, значит, постоянная времени усилителя равна длительности сигнала. Особенно сильно затягивание при высокочастотном шуме — время релаксации согласно указанной полосе фильтра должно быть порядка 1/2я/в - К такому же выводу практически пришли и в § 3.5. Широкополосный фильтр в каждый момент времени I воспроизводит только текущее значение входного сигнала и не запоминает его предыдущие значения. Оптималь­ный фильтр обязан обладать памятью — запоминать, т. е. фак­тически затягивать, каждое мгновенное воздействие на вре­мя Ти. Следовательно, опять ожидаем увеличения эффективной длительности выходного сигнала на Тп равного в зависимости от характера шума временам Тс либо 1/2л/в (§ 3.5). Впрочем, зачем «ожидать»: нам известны и частотная, и переходная ха­рактеристики оптимального фильтра, которых вполне достаточ­но для расчета формы выходного сигнала при известной фор­ме входного.

Выходной сигнал оптимального фильтра — это всегда сим­метричный сигнал. Такая интересная особенность оптимального фильтра является однозначным следствием его частотной ха­рактеристики, комплексно-сопряженной со спектром сигнала (3.47):

*(/)=*с*Ш/в; |*(/)| = М/)|/в;

Подставляя эту характеристику в обратное фурье-преобразова - ние (3.29), получаем выражение для выходного сигнала:

Оо

Ис (t) = jj ес (/) * 00 cos (со* + 1|)с + ■фу) df =

О

Сс

^ jj^lcosoyAtdi* At — t — £м. (3.181)

О

Чтобы получить максимальный сигнал (3.181), выбираем фазовую характеристику оптимального фильтра так, чтобы в некоторый момент времени t~tyi все гармоники на выходе до­стигали своего максимального (амплитудного) значения (см. § 3.2). При этом фазы входного сигнала и усилителя взаимно уничтожились и не входят в выражение для uc(t). Косину­соиды— функции четные, поэтому при смещении от максимума tM вправо и влево на один и тот интервал времени At— = {t—fM) сигнал падает в одинаковое число раз (3.181).

Расчет выходного сигнала можно проводить также с по­мощью импульсной характеристики по (3.141). Эта методика особенно удобна и наглядна при белом шуме. Ведь в этом слу­чае импульсная характеристика повторяется форму сигнала, так что (3.141) преобразуется к весьма простому виду:

Сс оо

«с (*) — ] ес (t) h{t — x)dx=Ycec (т) ес (t - х) dx. (3.182)

—со —ос

С помощью подобного интеграла (см. § 2.2) было дано опре­деление функции корреляции для шума (2.47), поэтому выход­ной сигнал оптимального фильтра, настроенного при белом спектре шумов, является фактически корреляционной функцией входного сигнала. Воспользуемся (3.182), поскольку конкрет­ный расчет начнем, как всегда, со случая белого шума.

Белый шум. Расчет формы выходного сигнала при прямо­

Угольном входном импульсе показан на рис. 3.20. Если прово­дим опрос до момента прихода сигнала на вход t^.—Гс/2 (рис. 3.20, а, б), то выходной отклик, естественно, равен нулю. Импульсная характеристика (рис. 3.20, в) относится к моменту опроса t—Q. К этому моменту времени на ФПУ успевает по­пасть половина энергии сигнала. Выходной отклик нашего фильтра-интегратора равен указанной энергии (заштрихован­ная площадь), определяемой пересечением функций ес(т) и h{t—x)~ec(t—х)/Тс. Это вытекает также из (3.182). Из ска­занного следует, что выходной сигнал линейно возрастает со временем на интервале —Гс/2...Гс/2, причем в момент ^7с/2 он достигает своего максимума. В этом случае опрос проведен сразу по окончании действия входного импульса, а с^м импульс полностью укладывается в «память» фильтра

Рис. 3.20. Графический метод расче - Рис. 3.21. Графический метод рас - та выходного сигнала (входной им - чета выходного сигнала {входной пульс — прядюугольный) импульс — косинус-квадратный)

(рис. 3.20, г). Если опрос производится позже при 1>Тс/2, то выходной отклик начинает линейно падать (рис. 3.20, д). При С^ЪТс/2 выходной сигнал опять становится равным нулю, так как слишком поздно проводится опрос и глубины памяти фильтра уже не хватает, чтобы запомнить прошедшее (давно прошедшее) входное воздействие (рис. 3.20, е). Так получается треугольная форма выходного сигнала (рис. 3.20, ж).

Эта графическая методика поясняет расчет выходного сиг­нала при любой форме входного импульса, например косинус - квадратной (рис. 3.21), Выходной сигнал по (3.182) опреде­ляется площадью под кривой ес(т)ес(*—т) (рис. 3.21, заштри­хованная область). Поэтому, как только кривые ес(х),ес^—т) начинают пересекаться, сигнал становится отличным от нуля и при совпадении кривых достигает максимума. Рассчитанный по такой методике выходной сигнал представлен на рис. 3.21,^, кривая 1. Оптимальный фильтр не перестает приятно удивлять нас сюрпризами: он сохраняет на своем выходе форму сигнала почти косинусквадратной. Для доказательства на рис. 3.21,^ штриховой линией показан квадрат косинуса, кривая 2. Незна­
чительное различие кривых наблюдается только на «хвостах». Конечно, оптимальный фильтр не может ИДТИ против Природы его ограниченная полоса приводит к некоторому растягиванию входного колоколообразного импульса, длительность по уров­ню 0,5 увеличивается в 1,28 раза и почти во столько же (точ­нее в Г,33 раза) уменьшается амплитуда. Как видим, наши ожидания о затягивании отклика полностью подтвердились.

Высокочастотный шум. При небелом шуме приходится поль­зоваться обратным фурье-преобразованием (3.178). Подставим в эту формулу спектр шума 0= ^ГУ/в3. Спад подынтеграль­ной функции ёс2/© происходит за счет члена @ на низких ча­стотах ~/в, где спектр сигнала еще постоянный, ес(П»1. Поэтому получаем

(3.183)

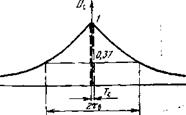
С помощью (3.183) на рис. 3.22 построен сигнал на выходе фильтра, оптимизированного для рассматриваемого случая ВЧ-шумов. Опять ожидания по поводу затягивания отклика полностью подтвердились.

С функцией (3.183) встречаемся второй раз — в § 3.5 она была получена для импульсной характеристики рассматрива­емого сейчас фильтра (3.146). Совпадение понятно: подынте­гральные функции (3.146), (3.183) различаются только множи­телями ес(И, £с2(/), а при fв<C/c эти множители одинаковы, еР;«есг«1. Таково математическое объяснение. Физическое объяснение тоже очевидно. Входной импульс значительно ко­роче постоянной времени фильтра тэ, так что его можно счи­тать дельтаобразным импульсом. Поэтому сигнал на выходе рассматриваемого фильтра воспроизводит форму его им­пульсной характеристики и совсем не зависит от формы корот­кого входного сигнала.

Низкочастотный шум. Как всегда, фильтр при таком шуме настраиваем на сигнал колоколообразной формы (поскольку задача оптимизации для прямоугольной формы сигнала здесь

Рис. 3.22. На выходе опти­мального фильтра при вьгсоко-

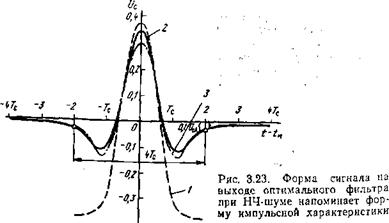
Некорректна, см. § 3.3). В § 3,5 удачно «угадана» импульсная характеристика такого фильтра. Теперь попытаемся «угадать» и форму выходного сигнала. Опять исходим из того, что главное отличие фильтра при НЧ-шуме в том, что он не пропускает по­стоянную составляющую. Значит, из косинус-квадратного сиг­нала с эффективной длительностью 1,28 Тс, который наблю­дается на выходе фильтра для белого шума, надо вычесть по­стоянную составляющую. Так приходим к кривой 1 на рис. 3.23. Точный расчет проводится с помощью обратного фурье-преоб - разования (3.181). Подставляя в эту формулу спектр шума faff и спектр колоколообразного входного сигнала ес=-л2 sin х/х(л2~х2), x=27ifTc, получаем

Uс = 2SECХТсКоcos (цAtdf — —^ c°s dx, о ос

Оо

Т г о с - АГо А f sin2 К X „At.

UC — SEC — я4 - тт-s---- ?Г2—соsa; ^dx —

Я J х (ri —х ) х„ Тя

О

= SEcAKo' J х{яа — х*у COSXjTj-rfA:!

(3.184)

Здесь согласно § 3.3 введен коэффициент усиления Ка (3.65):

ЯЯо/Ян=я/Со/2я/н7с = Kofdfн — Ко', xH=2nfaTc. (3.185)

Нормировку коэффициента усиления при НЧ-шуме (см. § 3.3) надо проводить именно к величине Ко'. Поэтому выражение в фигурных скобках (3.184) дает относительную форму сигна­ла— на выходе фильтра с единичным усилением Ко' — 1- Исхо­дя из этого и построена кривая 2 на рис. 3.23. Как видно из

Рисунка, удалось угадать форму положительного пика вы­ходного сигнала. А эго основное: именно положительный пик

(значение его амплитуды) определяет срабатывание порогового устройства. Дифференцирующий характер фильтра привел к появлению отрицательных выбросов. Правда, найти их форму не удалось. Она определяется спадом к(/) в области низких частот, а не только фильтрацией постоянной составляющей, как это считалось при лостроении кривой 1. Отрицательные выбро - сы медленно релаксируют до нулевого значения, длительность сигнала по уровню 0,5 составляет примерно 4Тс.

Прослеживается любопытная закономерность: колоколооб­

Разный сигнал оказался тестом для определения относительной формы импульсной характеристики оптимального фильтра, на­строенного на этот сигнал. Стоит подать такой «колокольчик» на вход фильтра, как тотчас его выходной сигнал воспроизве­дет (почти воспроизведет) относительную форму импульсной характеристики. Это справедливо не только для случая ВЧ-шу - ма (когда правило выполняется при любой форме входного им­пульса), не только для случая белого шума (когда ес({) и &(Д/), и «с(0> как братья-близнецы, все являются косинусоида­ми), но и для случая НЧ-шума. Чтобы это доказать, с рис. 3.17 на рис. 3.23 была перенесена импульсная характери­стика фильтра при НЧ-шуме (кривая 3), только она вдвое уменьшена по амплитуде и растянута по оси времени на одну треть. Поведение обеих кривых 2 и 3 весьма «единодушно».

Подведем итог. Форма сигнала на выходе оптимального фильтра всегда симметрична. При белом шуме выходной сигнал является корреляционной функцией входного и в классическом случае прямоугольного входного им­пульса имеет треугольную форму. При НЧ-шуме на фронте и спаде выход­ного сигнала появляются отрицательные выбросы, поскольку оптимальный фильтр в этом случае обладает дифференцирующими свойствами. При ВЧ - шуме выходной сигнал не зависит от формы входного и воспроизводит от­носительную форму импульсной характеристики фильтра. Впрочем, при по­даче на вход косинус-квадратного сигнала относительная форма импульсной характеристики воспроизводится при любом характере шума — низкочастот­ном и белом (в последнем случае входной и выходной сигналы и импульс­ная характеристика имеют практически одинаковую косинус-квадратную форму).

Ограниченная полоса оптимального фильтра приводит к затягиванию вы­ходного сигнала: при белом и НЧ-шуме его длительность по уровню 0,1 воз­растает обычно в 1,5...2 раза, а длительность по полуширине примерно на 30%, При преобладании ВЧ-шума, характеризующегося граничной частотой? в, полоса оптимального фильтра значительно уже полосы входного сигнала, поэтому сигнал на выходе затягивается особенно сильно — он экспоненци­ально релаксирует с постоянной времени 1/2 я/*