ФОТОЭЛЕКТРИЧЕСКОЕ. ПРЕОБРАЗОВАНИЕ. СОЛНЕЧНОЙ ЭНЕРГИИ
ФИЗИЧЕСКИЕ ПРИНЦИПЫ ФОТОЭЛЕКТРИЧЕСКОГО. ПРЕОБРАЗОВАНИЯ СОЛНЕЧНОГО ИЗЛУЧЕНИЯ
Фотоэлектрическое преобразование электромагнитного излучения Солнца в электрическую энергию происходит в полупроводниковых фотоэлектрических (ФЭ) ячейках (фотоэлементах). Фотоэлектрические элементы на базе кристаллического кремния получили наибольшее распространение. Поэтому мы проиллюстрируем физические основы преобразования солнечной радиации именно на их примере. Фотоэлектрические элементы на основе других полупроводниковых материалов функционируют в соответствии с точно такими же принципами.
Полупроводники могут быть классифицированы как собственные или легированные, в соответствии с природой носителей заряда. Легированные полупроводники могут быть N-типа (с электронами в качестве основных носителей заряда) или P-типа (с дырками, которые ведут себя, как положительно заряженные частицы, в качестве основных носителей заряда).
Здесь приводится описание процессов, имеющих место в полупроводниках, и в основном это описание поведения электронов и дырок. Читателям, заинтересованным в более глубоком понимании этих вопросов, мы рекомендуем обратиться к любой монографии по физике твердого тела, например [9 - 11]. В этой главе мы представляем упрощенное объяснение в соответствии с соответствующими публикациями, например [12].
Кремний (Si), атомы которого имеют на внешней, валентной оболочке четыре электрона, обладает кристаллической структурой типа алмаза, в которой каждый атом кремния окружен четырьмя его самыми близкими соседями. Четыре электрона на внешней оболочке каждого атома кремния (валентные электроны) образовывают ковалентные связи с соседями. Энергия свободного электрона, не подверженного воздействию внешних сил, может принимать любые значения.
Но энергия электрона в кристалле кремния может иметь только определенные значения при его движении в периодическом потенциальном поле. Эти энергетические уровни подразделены на зоны, названные «зонами разрешенной энергии». Зоны разрешенных энергий разделены «зонами запрещенных энергий», которые принято называть «запрещенной зоной».
Ниже перечислены зоны, играющие важную роль: валентная зона (самая высокая зона, заполненная при наименьших температурах), самый высокий запрещенный промежуток (запрещенная зона) и зона проводимости (самая низкая незанятая зона при самых низких температурах).
Валентная зона состоит из энергетических состояний валентных электронов. Вследствие того, что число этих состояний в точности соответствует числу валентных электронов во всем кристалле, при низких температурах эти зоны будут все заняты. С точки зрения роста энергии валентная зона следует за зоной проводимости. При повышении энергии электронов, находящихся в валентной зоне, до некоторой величины они переходят в зону проводимости, уровни в которой не заняты при низких температурах. Различия между индивидуальными уровнями энергии являются неизмеримо малыми в зоне разрешенных энергий.
Самый высокий энергетический уровень валентной зоны обозначен Ev, самый низкий уровень зоны проводимости обычно обозначается Ес. Таким образом, ширина запрещенной зоны составит величину АЕа = Ес - Ev.
Другой важный энергетический уровень — так называемый уровень (энергия) Ферми Е/;. Его более детальное рассмотрение не входит в задачи настоящей книги. Читатели, которых интересует этот вопрос, могут обратиться к специальной литературе, в частности к упомянутым выше монографиям [9-11].
В собственном полупроводнике (например, в чистом кремнии) уровень Ферми находится в середине запрещенной зоны. При самых низких своих состояниях валентные электроны занимают полностью все уровни в валентной зоне и не могут участвовать в проводимости электрического тока. При поступлении энергии, например тепловой энергии (фононы) или света (фотоны), некоторые электроны возбуждаются и переходят в зону проводимости, то есть они освобождаются от своих атомов. И валентная зона, и зона проводимости становятся частично занятыми зонами. Эта ситуация иллюстрируется энергетической диаграммой, электроны оставляют энергетические уровни в валентной зоне и занимают уровни с более высокой энергией в зоне проводимости. Эти электроны облегчают проводимость электрического тока, они могут свободно двигаться всюду по кристаллической решетке. После ухода электронов в зону проводимости в валентной зоне остаются свободные места. Свободные электроны могут быть захвачены в этих свободных местах, на энергетической диаграмме показан процесс возвращения электрона в это место с уровня в зоне проводимости. Электроны соседних атомов могут перемещаться в эти свободные места. Таким образом, образовавшиеся вакантные места, остающиеся после ухода электрона, могут передвигаться по кристаллу, этот процесс может повторяться, позволяя пустующим местам, «дыркам», перемещаться.
В электрическом поле свободные электроны перемещаются против направления электрического поля, так как они имеют отрицательный электрический заряд. Это означает, что свободные места перемещаются по направлению электрического поля. Вакантное место, таким образом, ведет себя как частица с положительным зарядом и массой, отличающейся от массы свободного электрона. Эту квазичастицу так и принято называть «дыркой».
В собственном полупроводнике уход одного электрона из валентной зоны приводит к образованию одной дырки, число свободных электронов и дырок равны. Кристалл в целом остается электрически нейтральным. Если пара «элект - 80
рон - дырка» образуется падающим фотоном (то есть квантом света), то энергия фотона должна быть равной или больше, чем ширина запрещенной зоны. Фотоны с более низкой энергией проходят через полупроводник, а фотоны с большей или равной энергией генерируют электронно-дырочные пары. Ширина запрещенной зоны в кремнии составляет величину приблизительно АЕа «1.1 eV, т. е. кремний прозрачен для фотонов более низких энергий, которые беспрепятственно проходят через материал. Длины волн, соответствующие этим энергиям, больше чем приблизительно Л > 1100 пт. Сравните с хорошо известной формулой для энергии фотона
г, he Е = hv = —, Л
где И - константа Планка; v - частота; с — скорость света).
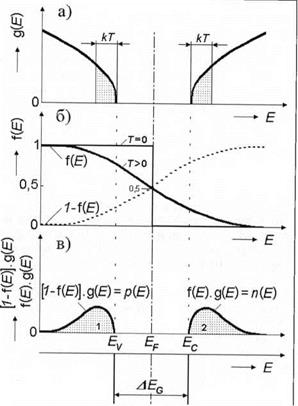
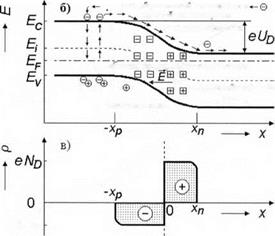
На рис. 7.1 в графической форме представлены наиболее важные характеристики собственного полупроводника. Рис. 7.1, а иллюстрирует функцию g(E), характеризующую плотности состояний (число состояний в интервале единицы энергии) в валентной зоне и зоне проводимости, соответственно, как функцию энергии.
Функция j{E) (рис. 7.1, б) определяет вероятность занятия электроном состояния с энергией Е. Величина I - f(E) является вероятностью того, что данное состояние остается незанятым.
Вероятность того, что частица будет обладать энергией, соответствующей уровню Ферми Ef, равна 0.5. Электроны принадлежат к классу частиц, названных фермионами. Их поведение соответствует теории статистики Ферми - Дирака [9, 10, 58]. Это означает, что функция разделения на рис. 7.1, б может быть математически выражена как
где к - константа Больцмана; Т — абсолютная термодинамическая температура.
На рис. 7.1, б представлена функция f(E)g(E) = п(Е) (концентрация электронов в зоне проводимости). А также функция [/ - f(E)]g(E) = р(Е), (концентрация дырок в валентной зоне при температуре, отличной от нуля).
На рис. 7.1, в представлена функция f(E)g(E) = п(Е) (концентрация электронов в зоне проводимости), а также функция [I - f(E)]g(E) = р(Е), (концентрация дырок в валентной зоне при температуре, отличной от нуля).
Пунктирные области 1, 2 под кривыми пропорциональны этим концентрациям. В собственном полупроводнике эти области равны.
Если мы заменим атомы Si в кремниевом кристалле атомами некоторых элементов пятой группы периодической системы, имеющими пять валентных электронов (например, As, Р, Sb), то четыре из этих валентных электронов образуют ковалентные связи с соседними атомами кремния. Пятый электрон будет
|
Рис. 7.1. Модель электронов и дырок в собственном полупроводнике |
слабо связан с атомом примеси. Этот легированный полупроводник называют полупроводником n-типа («negative»). При подведении относительно небольшого количества энергии этот электрон «отрывается» от атома (на энергетической диаграмме это показано как переход в зону проводимости). Эти пятивалентные атомы называют донорами, так как они поставляют свободные электроны. Присутствие атомов такой примеси показано на энергетической диаграмме как формирование локальных энергетических уровней, лежащих в запрещенной зоне близко к самому низкому уровню (дну) зоны проводимости Ес.
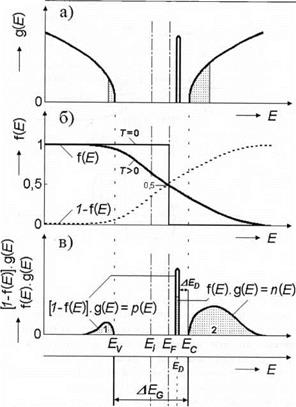
Рисунок 7.2 представляет функции для полупроводника n-типа, аналогично функциям на рис. 7.1 для собственного полупроводника. Донорный энергетический уровень обозначается как Ер. Энергия ЛЕр. требуемая для перехода электрона с этого уровня в зону проводимости, является относительно малой величиной, порядка Л Ер « 0.01эВ. При комнатной температуре (тепловая энер-
гия, поставляемая электрону, составляет приблизительно кТ = 0.025 эВ) электрон может легко быть возбужден и переведен в зону проводимости. В этом случае уровень Ферми сдвигается к более высоким энергиям (рис. 7.2,6). Из-за низкой величины AEd атомы донорной примеси ионизируются при комнатной температуре (и даже при более низких температурах), формируя область положительного заряда.
|
Рис. 7.2. Модель электронов и дырок в полупроводнике п-типа |
Концентрация электронов в зоне проводимости намного выше, чем концентрация дырок в валентной зоне, потому что при тепловом образовании дырок электроны должны перепрыгнуть через всю запрещенную зону (неосновные носители).
Область 2 на рис. 7.2,в больше, чем область 1 (заметим, что концентрация электронов равна сумме концентраций дырок и ионизированных доноров).
|
|
||
|
|||
|
|||
|
|||
|
|||
|
|||
![]()
рекомоинационныи ток электронов
тепловой ток электронов
зона проводимости
j f ооласть пространственного заряда
запрещенная зона
валентная зона
-еЛ/д
Рис. 7.3. Модель р-п перехода
При замене атомов Si в кремниевом кристалле атомами элементов третьей группы периодической системы (например, атомами В, Al, Ga), в кристаллической решетке образуется область, содержащая атомы только с тремя валентными электронами. Для этих атомов одна связь не будет насыщена и не будет скомпенсирована четырьмя соседними атомами кремния.
Она будет вести себя как «дырка». Вследствие теплового движения валентный электрон от соседнего атома кремния может попасть в эту незанятую связь, и дырка будет перемещаться по кристаллу, как это уже описано выше. Полупроводник, легированный таким образом, называют полупроводником p-типа (positive). Примеси, формирующие электронные ловушки, называют акцепторами (рис. 7.3).
Такое поведение показывается на энергетической диаграмме таким же образом, как и для полупроводника n-типа на рис. 7.2.
Акцепторный энергетический уровень Еа образуется в запрещенной зоне ближе к верхнему пределу валентной зоны. При подводе относительно малого количества энергии А ЕА электроны из валентной зоны могут быть захвачены на этом уровне.
Дырка, образованная таким образом в валентной зоне, может теперь перемещаться свободно по кристаллу. Поэтому в полупроводнике p-типа концентрация дырок намного выше, чем концентрация свободных электронов (неосновные носители) и энергетический уровень Ферми перемещается к более низким энергиям.
В кристалле может иметь место неоднородное распределение концентрации примеси. Например, некая область может быть легирована сильнее, чем остальные. Кроме того, можно легировать некоторые области кристалла примесями группы 5, а некоторые элементами группы 3. В обоих случаях, свободные носители заряда (электроны и дырки) имеют тенденцию, в соответствии с законами диффузии, перемещаться из области с более высокой концентрацией в области с более низкой концентрацией, таким образом устанавливая однородное распределение. Однако если свободные носители удаляются из некоторых областей, твердо фиксированные заряды ионизированной примеси с противоположным зарядом остаются в их первоначальном положении, формируя заряженную область. В результате этих процессов в кристалле формируются относительно сильные локальные электрические поля, даже при том, что кристалл остается в целом электрически нейтральным. Эти области предотвращают дальнейший отток свободных носителей из областей с более высокой концентрацией, и система достигает равновесия.
Крутой р-n переход - специальный пример неоднородного распределения примеси (идеализированная модель, см. рис. 7.3). Такой переход образуется, когда одна часть кристалла легируется как полупроводник p-типа, а смежная часть как полупроводник n-типа. В переходе градиент концентрации свободных носителей — это градиент N в направлении перехода (идентично направлению х на рис. 7.3,а), где /V/) - концентрация доноров, a Na - концентрация акцепторов.
Как уже упоминалось, некоторые свободные электроны переместятся из области n-типа в области p-типа, а некоторые дырки переместятся в противоположном направлении. Жестко фиксированные заряды ионизированной примеси, остающиеся на своих местах в кристалле, формируют область объемного заряда (положительного заряда в полупроводнике n-типа на рис. 7.3,в). Электрическое поле, образующееся между р и п областями, препятствует дальнейшему перемещению в обе стороны свободных носителей. В состоянии равновесия уровень Ферми должен быть уравновешен повсеместно, по всему кристаллу так, чтобы в области перехода зоны изогнулись. Идеализированная ситуация иллюстрируется на рис.7.3,6. Ширина р-n перехода задана точками хр и х„, UD - разность потенциалов между различным образом легированными областями (так называемый диффузионный потенциал).
Р-n переход функционирует как простой полупроводниковый диод. Однако эта система достигает скорее динамического, а не статического равновесия. При температурах Т> О К электроны и дырки непрерывно генерируются и рекомбинируют во всем объеме полупроводника, как показано на рис. 7.3,6. Мы проиллюстрировали только электронные потоки, отмечая, что потоки дырок ведут себя аналогичным способом. Некоторые электроны в полупроводнике n-типа могут иметь энергию выше, чем диффузионный потенциал Up - Эти
электроны могут пересечь р-n переход и проникнуть в полупроводник Р-типа, где они рекомбинируют со свободными дырками. Этот поток называют рекомбинационным потоком. В то же самое время свободные электроны и дырки генерируются в полупроводнике p-типа и ускоряются в электрическом поле р-п перехода к полупроводнику n-типа. Этот поток называют тепловым или диффузионным потоком. Без приложения внешнего поля эти потоки в противоположных направлениях равны и не определимы внешне. Если приложен внешний потенциал и электрическая цепь замкнута, равновесие нарушено. Если положительный потенциал приложен на стороне p-типа, кривизна зон меняется, потенциальный барьер UD уменьшен на AV, и потоки электронов к полупроводнику p-типа (и дырок в противоположном направлении) преобладают. Р-n переход, таким образом, включен в прямом направлении.
Если положительный потенциал приложен к стороне n-типа, потенциальный барьер Uо становится выше, рекомбинационный ток снижается, и тепловой ток преобладает. Тепловой ток, однако, имеет меньшую величину из-за более низкой концентрации электронов в полупроводнике р-типа. Р-n переход в этом случае сориентирован в обратном направлении.
Теперь мы переходим к принципу фотоэлектрического преобразования солнечной энергии непосредственно. Это преобразование имеет место в полупроводниковой фотоэлектрической ячейке, где энергия падающего фотона преобразуется в электрическую энергию. Фотоэлемент, в основном, представляет собой большой диод, где р-n переход размещается между фронтальной и тыльной сторонами элемента, параллельно лицевой поверхности. Если к фотоэлектрической ячейке поступают фотоны с энергией выше, чем ширина запрещенной зоны, то каждый из этих фотонов образует электронно-дырочную пару. Таким образом, эти фотоны передают свою энергию кристаллу и поглощаются. Если энергия фотона больше ширины запрещенной зоны, имеющийся избыток энергии передается колебаниям решетки и преобразуется в тепловую энергию, которая увеличивает температуру материала полупроводника. Электроннодырочные пары, создаваемые в области р-n перехода, разделяются электрическим полем Ё между фиксированными неподвижными пространственными зарядами. Дырки ускоряются в направлении поля, а электроны в противоположном направлении. Между противоположными полюсами фотоэлемента образуется электрический потенциал. При включении фотоэлемента в электрическую схему через цепь потечет постоянный ток. Таким образом, фотоэлемент становится источником электроэнергии.
Эта ситуация иллюстрируется схематически на рис. 7.4. Этот рисунок изображает диаграмму энергетических уровней в полупроводниках р-типа и п-типа. Рисунок 7.4,6 иллюстрирует выравнивание значений потенциала Ферми и изгиб зон в области р-n перехода в неосвещенной фотоэлектрической ячейке.
Здесь изображены также рекомбинационные и тепловые токи в состоянии равновесия, области объемного заряда и диффузионный потенциал t/д. В темноте (без освещения) фотоэлектрическая ячейка ведет себя как полупроводниковый диод.
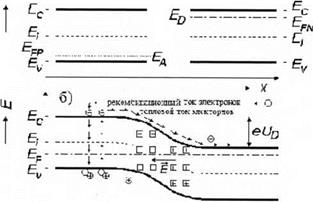
Рис. 7.4,в иллюстрирует ситуацию, имеющую место после освещения фотоэлемента, не соединенного с электрической цепью. Поступающие фотоны нарушают изначальное равновесие и создают новое равновесие. Генерация электронов и дырок возрастает. Образующиеся электроны и дырки ускоряются в области электрического поля р-n перехода в направлении, указанном стрелками (фактически в направлении, обратном току от отрицательного к положительному полюсу). Сторона p-типа становится положительно и n-типа отрицательно заряженными. Потенциальный барьер Ud уменьшается и уровни Ферми в областях p-типа и n-типа разделяются. Различие в значении потенциалов между областями эквивалентно фотоэлектрическому напряжению, обозначенному на рисунке. В пределе это напряжение может соответствовать первоначальному
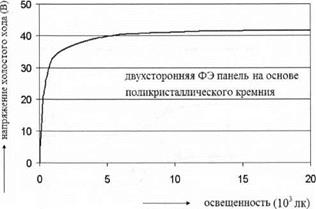
изгибу зон, которое в кремниевых фотоэлементах обычно составляет приблизительно Up « 0.6 V. Дальнейшее увеличение интенсивности освещения не увеличивает напряжение разомкнутой цепи, как это показано на рис. 7.5.
|
Рис. 7.5. Зависимость напряжения холостого хода от освещенности фотоэлектрической панели (солнечные элементы соединены последовательно-параллельно) |
Это происходит потому, что фотоэлектрический потенциал и потенциал объемного заряда компенсируются в р-n переходе. Далее, в р-n переходе направленное движение образованных электронов и дырок прекращается, и они более не разделяются. Процесс может также интерпретироваться таким образом: уменьшение потенциального барьера Up при освещении приводит к увеличению рекомбинационного тока электронов в полупроводник p-типа и возрастанию рекомбинационного тока дырок в противоположном направлении. Это компенсирует увеличенный диффузионный поток, вызванный разделением образованных электронов и дырок в электрическом поле Е между фиксированными заряженными областями в р-n переходе. Возникшее фотоэлектрическое напряжение способствует установлению нового равновесия.
Если мы соединим освещенный фотоэлемент с электрической цепью, то соединение двух полюсов приведет к уменьшению напряжения (электродвижущей силы источника). Это, в свою очередь, вызовет изменение в изгибе зон так, что потенциальный барьер Up увеличится снова.
Рекомбинационный поток, таким образом, будет уменьшаться, и тепловой поток будет преобладать из-за разделения образованных электронов и дырок в электрическом поле Е между неподвижными пространственными зарядами. Сумма двух потоков не будет равна нулю, и образующийся ток будет поставляться в электрическую цепь фотоэлемента, который начинает функционировать в данном случае как источник энергии.
е

![]()
 со
со
р
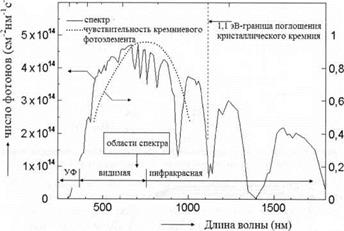
Поскольку ширина запрещенной зоны кристаллического кремния AEg » 1.1 эВ, то кремниевые элементы будут чувствительны к фотонам видимой и близкой инфракрасной области солнечной радиации с длинами волны Я < 1100 нм.
На рис. 7.6 приведен спектр солнечного излучения после прохождения через атмосферу с обозначением длин волн и энергии фотонов. Здесь также указана ширина запрещенной зоны кремния или, другими словами, край поглощения.
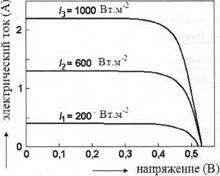
Рисунок 7.7 представляет вольтамперные характеристики освещенного фотоэлектрического элемента на основе кремния в электрической цепи. Индивидуальные кривые соответствуют различной интенсивности освещения. Пересечения кривых с вертикальной осью дают токи короткого замыкания, соответствующие «нулевому» сопротивлению во внешней цепи (или, другими словами, к короткому замыканию обоих полюсов фотоэлемента). Если нагрузка в цепи увеличивается, мы двигаемся от этих пунктов вдоль кривых в направлении увеличивающегося напряжения (направо).
Пересечения кривых с горизонтальной осью дают напряжение разомкнутой цепи, то есть они соответствуют «бесконечному» внешнему сопротивлению цепи, или разомкнутой цепи. Оптимальная нагрузка элемента соответствует сопро-
|
Рис. 7.7. Вольтамперные характеристики освещенного солнечного элемента при различных уровнях засветки и температуре t = 50°С |
|
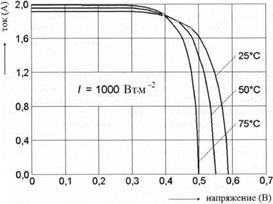
Рис. 7.8. Вольтамперные характеристики освещенного фотоэлемента на основе кристаллического кремния при различных температурах и постоянной интенсивности освещения I = 1000 Вт м ~2 |
тивлению, при котором произведение напряжения и тока максимальны, так называемая рабочая точка на вольтамперной характеристике (прямоугольник, определяемый осями и рабочей точкой, имеет максимальную площадь). В этом случае фотоэлемент выдает максимально возможную мощность.
На рис. 7.8 представлены вольтамперные характеристики фотоэлементов на основе кристаллического кремния в зависимости от температуры при постоянном освещении.
Можно заметить, что ток короткого замыкания увеличивается с увеличением температуры, но напряжение разомкнутой цепи понижается. Оптимальные рабочие точки обозначены кружками на кривых. Максимальная мощность
фотоэлемента при постоянном освещении и, следовательно, коэффициент полезного действия, уменьшается с увеличением температуры.
Описанный механизм фотоэлектрического преобразования солнечного излучения может реализовываться только в полупроводниковых материалах, которые в отличие от металлов имеют некоторую запрещенную зону. Однако в отличие от диэлектриков ширина запрещенной зоны у полупроводников не столь велика, что определяет их специфические свойства.
Термин «полупроводники» часто понимают как совокупность нескольких наиболее типичных групп веществ, полупроводниковые свойства которых четко выражены уже при комнатной температуре (300 К).
Полупроводники при комнатной температуре имеют значения удельного сопротивления в пределах 10”6 - 109 Ом м (промежуточное положение между металлами и диэлектриками). Ширина запрещенной зоны у полупроводников лежит в диапазоне 0,1 - 3,0 эВ.
Удельная проводимость полупроводников в сильной степени зависит от типа и концентрации содержащихся в них примесей и дефектов. Для полупроводников характерна чувствительность к свету, электрическому и магнитному полям, радиационному воздействию, давлению и др.
В полупроводниках может наблюдаться смешанный тип химических связей: ковалентно-металлический, ионно-металлический и др.
К полупроводникам можно отнести широкий круг химических элементов и химических соединений:
• элементарные полупроводники: германий, кремний, селен, теллур и др.;
• соединения типа SiC;
• соединения типа А3В5 (например, арсенид галлия GaAs);
• соединения типа А2В6 (например, ZnTe, ZnSe, CdTe, CdS и т. п);
• окислы и сульфиды ряда металлов: NiO, Cu20, CuO, CdO, PbS и др.;
• тройные соединения: CuInSe2, CuSbSr, CuFeSe2, PbBiSe3 и др.;
• твердые растворы типа GeSi, GaAsi_x Рх и др.
Полупроводники могут быть кристаллическими или аморфными. Для изготовления фотоэлементов до настоящего времени использовались моно или поликристаллические полупроводники (кремний и в некоторой степени арсенид галлия), а также полупроводники в аморфном состоянии.
1. Элементы IV группы периодической системы элементов Менделеева германий и кремний наиболее полно изучены и широко применяются как в полупроводниковой электронике, так и в солнечной энергетике. Атомы этих элементов, обладая 4 валентными электронами, образуют кристаллические решетки типа алмаза с ковалентной связью атомов. Сам алмаз в некоторой степени также обладает полупроводниковыми свойствами, однако величина Eg для него значительно больше, чем у Ge и Si, и поэтому при Т = 300 К его собственная (не связанная с примесями или внешними воздействиями) электропроводность весьма мала.
2. К алмазоподобным полупроводникам относятся и соединения элементов III группы периодической системы (Al, Ga, In) с элементами V группы (Р, As, Sb), т. е. материалы типа А3В5 (GaAs, InSb, GaP, InP и т. п.). Атомы III группы имеют 3 валентных электрона, а V группы - 5, так что в целом число валентных электронов, приходящееся на 1 атом, в этих соединениях равно 4 (как у Ge и Si). Каждый атом образует 4 валентные связи с ближайшими соседями, в результате чего получается кристаллическая решетка, подобная решетке алмаза с той лишь разницей, что ближайшими соседями атома А3 являются атомы В5, а соседями атомов В5 - атомы А3. За счет частичного перераспределения электронов атомы А3 и В5 в такой структуре оказываются разноименно заряженными. Поэтому связи в этих кристаллах не полностью ковалентные, а частично ионные. Однако ковалентная связь в них преобладает, поэтому эти кристаллы по многим свойствам являются ближайшими аналогами Ge и Si.
3. Соединения элементов II и VI групп периодической системы - А2В6 (ZnTe, ZnSe, CdTe, CdS и т. п.) также имеют в среднем 4 валентных электрона на 1 атом, но ионная связь у них более сильно выражена. У некоторых из них ковалентная связь преобладает над ионной, у других она слабее, но и те, и другие обладают свойствами полупроводников.
4. В соединениях элементов VI группы с переходными или редкоземельными металлами (Ті, V, Mn, Fe, Ni, Sm, Ей и т. п.) преобладает ионная связь. Сочетание полупроводниковых и магнитных свойств этих соединений и их взаимное влияние интересно как с теоретической точки зрения, так и для практического применения в фотоэнергетике.
Многие органические соединения также обладают полупроводниковыми свойствами. В настоящее время проводятся исследования по практическому их использованию в качестве исходных материалов при получении солнечных элементов.
Из электрофизических параметров полупроводниковых материалов важнейшими являются: удельная проводимость (или величина, обратная ей - удельное сопротивление), концентрация электронов и дырок, температурные коэффициенты удельного сопротивления, ширина запрещенной зоны, энергия активации примесей, работа выхода, коэффициенты диффузии носителей заряда и другие. Для специального использования в некоторых случаях большое значение имеют коэффициент термо-ЭДС, а также коэффициент Холла и др.
К фундаментальным параметрам полупроводников относятся плотность, постоянная кристаллической решетки, коэффициент теплопроводности, температура плавления и др.
В отсутствие электрического поля дырка, как и электрон, будет совершать хаотические колебания, при этом происходят и обратные переходы электронов из зоны проводимости на свободные уровни валентной зоны (рекомбинация). Механизм генерации носителей и разделения электронно-дырочных пар, возникающих в полупроводнике под воздействием фотонов солнечного излучения, а также возникновения Э. Д.С. в солнечном элементе рассмотрены выше.
В настоящее время основным типом используемых на практике фотоэлектрических преобразователей являются «планарные» солнечные элементы, создаваемые на плоских пластинах полупроводникового материала, главным образом, кремния. Эти элементы далее собираются в модули, из которых собирают солнечные батареи. Основным действующим лицом в такой схеме является солнечный элемент.
Производственный цикл получения фотоэлектрических панелей - основной продукции, поставляемой сегодня на рынок, весьма сложен. Его можно разделить на три тоже сложных этапа.
1 этап - получения исходного полупроводника (преимущественно крем
ния) и подготовка пластин для последующего передела;
2 этап - получение солнечных элементов;
3 этап - получение солнечных модулей (панелей) с последующей по
ставкой их потребителю.
Многие крупные компании полагают для себя чрезвычайно выгодным объединить на своих предприятиях все три этапа, что позволяет улучшить координацию работ и обеспечить этапы получения СЭ и модулей бесперебойной поставкой сырья и полуфабрикатов.
В следующих главах мы рассмотрим каждый из этих этапов в отдельности.