ТЕРМОДИНАМИКА ПАССИВНОГО МЕМБРАННОГО ТРАНСПОРТА
Феноменологическое рассмотрение мембранного транспорта, основанное на термодинамике необратимых процессов, не касается молекулярной структуры мембраны и молекулярных механизмов транспорта. Термодинамика не столько объясняет физические явления, сколько организует наши знания, устанавливая связь между реальными физическими явлениями и их зависимость от параметров рассматриваемой системы. В данном случае термодинамика выявляет зависи - MocT^Tj^aHcriopTHbix потоков от усредненных характеристик растворов и мембраны [4", 7,-8].
"—Пассивный мембранный транспорт вещества определяется сЕлектиВной лцшни - цаемостью мембраны. Рассмотрим простейшую"' модеЛТ—Т№огённую мембрану, соприкасающуюся с двумя растворами (рис. 3.1). Потоки пересекают границы мембраны. Функцию диссипации внутри элемента dx мембраны можно записать в виде
Ra = Z//grad(-n,), (3.1)
І
Где J і — векторный поток t-ro вещества, ц» — его химический потенциал. Проинтегрировав это выражение по толщине мембраны, имеем
Ах
\ OTdx = Y, J^i (0) - (А*)] = Y. Jl • (3-2)
Х=0 х=Ах
Рис. 3.1. К термодинамическому рассмотрению мембраны
О і
Где (mu/— разность химических потенциалов на левой и правой гранйіцах, разделяющих мембрану и растворы. Естественно предположить, что значения ji на поверхности мембраны те же, что и в примыкающих растворах; напротив, йц/dx испытывает разрыв непрерывности. Поток вещества через границу пропорционален этой производной
/ = -Li(47)i==-Lii(77)ii>
Где индексы I и II относятся к раствору и к мембране.
Через мембрану идут потоки растворенных веществ и растворителя. Задача неравновесной термодинамики состоит в исследовании сопряжения этих потоков, для которых мембрана обладает различной проницаемостью.
В простейшем случае одного растворенного вещества
W = /5Am. s + ЛаЛЦш - (3.3)
Индекс 5 относится к растворенному веществу, w — к растворителю (вода). Если скорости движения растворенного вещества и растворителя в точке х равны vs и vw, а их концентрации равны С а и Cw, ТО
H = csus = hs, Jw = cwvw = hw. (3.4)
Химический потенциал растворителя можно представить в виде
Где р — давление, Vw — парциальный молярный объем растворителя, \icw и — зависящий и не зависящий от концентрации вклады в (і. Следовательно,
= [р (0) - P (Л*)] + К (0) - (Ах) = Vw Ар + . Как показывает теория осмотических явлений,
= - АФЮ = - Дя, где Ая— разность осмотических давлений. Следовательно,
ЛЦш = Vw (Ар - Ая) (3.5)
И аналогично
= + (3.6)
Введем среднюю концентрацию растворенного вещества Cs« '/г (0) — cs (Лх))і
Тогда
Щ = (3.7)
Из уравнений (3.3), (3.5) — (3.7) получаем
Ч = (/.V. + ISV.) АР + - Л^ш) Ал, (3.8)
Или
Ч^/уАр + УдАя, (3.9)
Где /у — полный объемный поток J у - / / s^s ^^ СщУw^w —
= ФЛ + Фsvs&^ + JsVs. (3.10)
Мы заменили здесь ст и cs их средними значениями сш и cs, а
Фш = cwVw « 1 > qps = csVs.
Поток /в есть обменный поток, т. е. поток растворенного вещества относительно воды:
LD*=b--IwVu*lb--Jg-=vs-vn, (3.11)
Где vs и vw — скорости переноса растворенного вещества и растворителя через мембрану. При большом избытке растворителя, т. е. при cwVw > csVs, имеем
/у» О... (3.12)
Таким образом, мы перешли к новым переменным, введя в качестве обобщенных сил не разности химических потенциалов, а разности давлений и осмотических давлений.
В линейной неравновесной термодинамике потоки /у и JD сопряжены
Ly = Lp Ар + LpD Ait, I
/D = LpDAp + LflAit. J ^^
Коэффициент Lp характеризует механическую фильтрационную емкость мембраны, т. е. скорость жидкости, приходящуюся на единицу разности давлений. LD выражает скорость жидкости на единицу разности осмотических давлений. Наконец,
, (Мдр. О
ЬпП "
— Дя
Является коэффициентом осмотического потока. Для идеальной полупроницаемой мембраны, не пропускающей растворенное вещество ни при каких значениях Ар и Ая, поток = 0. Следовательно,
И из (3.13) получаем при любых Ар и Ая
(Lp + LpD) Ар + (LpD + Ld) Ая = 0,
Откуда
LpЈ) = Lp = Lfit при этом Ая = Ар. В самом деле, из (3.13) следует, что
Если мембрана не идеальна и пропускает растворенное вещество, то
Р
Величина к является мерой селективности мембраны и варьирует от 0 при полном отсутствии селективности до 1 для идеальной полупроницаемой мембраны. Величину к можно назвать коэффициентом отражения [9]. Имеем
(» -(if^) - if— «і (3.14,
Vyv/A„_0 V vw /дл=0 lp
При к = 0 vs = vw, при к = 1 ws = 0, при 0 < к < 1 vs < vw и, наконец, при к < 0 ws > vw, т. е. речь идет об отрицательном аномальном осмосе. Перепишем выражение для Jv (см. (3.13)) в виде
Jv = Lp(Ap — KAn). (3.15)
Из (3.10), (3.11), (3.13) и (3.14) при csVs< 1 следует, что
/, = (1 —+ соАя, (3.16)
Где
І і —і2
Co = cs —— (3.17)
Up
Есть коэффициент проницаемости для растворенного вещества при нулевом объемном потоке. Очевидно, ЧТО
® = (-&-)/„-<>• (3.18)
Таблица 3.2 Коэффициенты «а и х для мембраны
Для идеальной полупроницаемой мембраны ю = 0, для неселективной мембраны Lpd = 0, со = csLd. Коэффициенты к и со легче определить экспериментально, чем LB. В стационарном состоянии (см. § 2.3) поток Jv= 0. Согласно (3.14)
Эритроцита человека
И со определяется из (3.18).
В табл. 3.2 приведены значения со и к для мембраны эритроцита человека [4]. Ьр в этом случае равно 0,92-10-11 см3/(дин-с).

Растворенное вещество
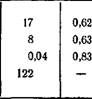
Мочевина Этиленгликоль Малонамид Метанол
Физический смысл феноменологических коэффициентов раскрывается с помощью представлений о трении [4, 9].
Х„
Dx
Сила, движущая воду в точке х мембраны
(3.20)
В стационарном состоянии уравновешивается силой трения воды о мембрану
Xqjtn
Где Ptam — коэффициент трения. Следовательно,
dy. w R
Dx ~PwmVw.
Поток воды в точке X
J =cmV,
W WW*
Где концентрация воды в мембране.
Коэффициент распределения воды между средой и мембраной равен
Имеем
DV-w $wmcw vw fgfiwm ^да^аfiwm
~ с™ ~ *
(3.25)
После интегрирования от 0 до Ад; получаем при Ая « 0 в левой части
В правой, считая Рдат и <р™ постоянными и учитывая (3.10),
Имеем
&х J V В /6
W w"wm v"wm д^.
Г ш щРаїт ^ __ У Г
} С ф
Следовательно,
(3.26)
Сравнивая это уравнение с первым уравнением (3.13) при Ал; = 0, находим
Ь-ЁОь - <»•»>
Аналогичным образом рассматривается движение растворенного вещества. Движущая сила Xs уравновешивается силой трения, т. е. силой взаимодействия вещества с матриксом мембраны и силой трения о воду
Xs = Xsm + Xsw — vs (PSK1 + psm) — UmPsa,. (3.28)
В этом случае для растворителя
Xw = Xwm - f - Xws — vw (Рдат + Pais) — ysPais - ' (3.29)
(3.30)
Коэффициент Трения Psu; близок к коэффициенту трения в выражении для коэффициента диффузии
%W = RT/D.
Согласно (3.3)
У d\lw ^ Pais/я і (Paiffi Pais) }а
TOC \o "1-3" \h \z л® J т ' т
Dx с™ с™
У ___ d\lg | (psw + Psm) Js
Dx ~ cT С»
Эти выражения для движущих сил эквивалентны обратным линейным соотношениям между силами и потоками
Хда = /?ц/а, + /?124, | (3 31)
Xs = R2Jw + R22J5 , J
О Psai г> Pias >
TOC \o "1-3" \h \z, К21 — — К12— "УНТ'
Lw s
_ Pais Рита
С
(3.32)
О _ Рsw + Psro "22 •
Расчет показывает, что коэффициенты и и со следующим образом выражаются через коэффициенты трения [4]:
(3.33)
Ks.. _ і coV$ Copst8, А*
I\s і
СО» , И « 1
Л* (Р„ + Psm) Lp <
В табл. 3.3 приведены коэффициенты трения для двух целлюлозных мембран [4].
Таблица 3.3 Коэффициенты треиия для целлюлозных мембран
^sm' дин-
SW*
ДИН'С
Wm'
Дин-с
Мембрана
Ю»
Ю13
10'«
Растворенное вещество
Visking для диализа
Dupont «wet gel»
Мочевина
Глюкоза
Сахароза
Мочевина
Глюкоза
8,30 8,52 8,55
1,68
0,66 1,89 3,25
0.28 0,78 1,12
0,065
0,23
0,65
0,0046 0,030 0,066
Сахароза
В дальнейшем была показана необходимость дополнения выражений, учитывающих трение, членами, характеризующими вязкое течение, зависящее от давления [10]. Дополненная теория дает лучшее согласие с опытом.
До сих пор мы рассматривали растворы неэлектролитов. Для биологии особенно существен транспорт ионов через мембраны, в частности, ионов Na+, К+, Са++ и Mg^.
Если имеются заряженные частицы, то в выражение для внутренней энергии входит электрическая энергия
DUe і = г|> de,
Где — электрический потенциал мембраны, е — заряд. Соответственно, вместо химического потенциала нужно рассматривать электрохимический потенциал
Ji, = \it + i|>, (3.34)
Где 9" — число Фарадея, z\ — валентность заряженной частицы.
Условие равновесия двух растворов, 1 и 2, разделенных мембраной, имеет вид
Iij» = А®. (3.35)
Или
Дцг + Zi&~ Дф = 0, (3.36)
Где А-ф — разность потенциалов между двумя сторонами мембраны. Имеем
А(1)
Дц, = ЯГ Inда — z^h^, (3.37)
Ai
Здесь а(/', fl(2) — активности, заменяемые в случае идеальных растворов концентрациями с'1», cf>.
В изотермической и изобарической системе в отсутствие химических реакций функция диссипации равна (ср. (3.1))
To = Zj{ grad (- Д,); (3.38)
І
Вместе с тем из уравнения Гиббса — Дюгема
SdT-Vdp + dvn = 0 і
Следует
Z Ci grad Уп = 0. (3.39)
Из уравнений (3.38) и (3.39) получаем
N-i с п-і
Та=Z С7' - 7") ^rad ^=£J' ^rad (- І*'). (3-4°)
І-I w г-i
Где — диффузионный поток t-x ионов. В простейшем случае одного электролита, дающего ионы двух сортов 1 и 2,
= А — h
! їй — b12grad Д2) ) ЇИ — ь22 grad Д2. j
И линейные соотношения имеют вид
/? = — Lugrad. __ .
/2 = — Li2 grad [■
Коэффициент Ln характеризует подвижность катиона, L22 — аниона, L\2 — взаимодействие разноименных ионов.
При наличии электрического поля Е = —grad и при однородной концентрации (grad рц = 0) имеем
Grad p,! = z\ST grad г|з = — zxg~E, grad \x2=== z29~ grad :
(3.42)
- z2TE, J
И уравнения (3.41) принимают форму
(3.43)
/? = {zxLu + z2Ly2)3~E,
J2 =(zjL 12+ Z2L22) 3~E
Электрический ток в системе описывается уравнением
«-і
I = I z. TJf, (3.44)
И в нашем простейшем случае получаем
/ = {z\Ln + 2Z1Z2L12 + zIL22) Г>Е. (3.45)
Следовательно, коэффициент электропроводности системы равен 8 = (*?*•„ + Ч^и + ^22) (3.46)
С другой стороны,
Jf = Cl (0j _ /й = с2 (и2 - 0в)
И, так как
Cl=V! Cs, c2 = v2cs, где Vi, v2 — стехиометрические коэффициенты, то имеем I = Z\SFV! CS (и, — wj + z23~v2cs (v2 — vw) = = ZiTViCsy 1 + z2g~v2csv2 — vwg~cs (v^, - f v2z2). (3.47)
Последний член в этой формуле равен нулю в силу электронейтральности раствора. Окончательно получаем
I = zl9Jl + z2&-J2, (3.48)
Где
Ji — v\csvu J2 = v2csv2.
Для нахождения феноменологических коэффициентов мы располагаем пока одним выражением (3.46). Второе выражение дает число переноса, определяемое соотношением
(3.49)
Grad «=0
В нашем случае, пользуясь (3.43) и (3.45), находим
Ti — 1 — t2 = = Z1 (z\Lll + z2L\2) ф 50)
Наконец, третье выражение получается из рассмотрения диффузии электролита в отсутствие тока
Поток нейтральной соли находим с помощью (3.41):
= ± = hfl "tn~Ll2l grad = gradc..
V, V2 v, v2 zfZ-jj+2z, z2t12 + z|Z-22
(3.51)
Написав
Grad ns= nssgradc„ где nss = d\isldcs, получим из (3.46), (3.50) и выражения (3.51)
V|D (iss
FGlF") '
(3.52)
-22 ■
-12 '
(z2r) '
(Iss
Vi v2D, gtit2
(iss ZXZ2&"2
В случае ионных растворов также можно представить феноменологические коэффициенты через коэффициенты трения [4, 7]. Ситуация здесь усложнена, так как число этих коэффициентов велико — уже для раствора NaCl в воде их шесть. Расчеты упрощаются, если мембрана сильно заряжена, и поэтому концентрация фиксированных противоионов в Матриксе мембраны много выше концентрации нейтральной соли. Подробное рассмотрение проблемы применительно к простым и сложным мембранам (последние представляют собой систему параллельных слоев с различными характеристиками) проведено в работах [4, 7]. Здесь мы не будем на нем останавливаться.
Таким образом, неравновесная термодинамика дает физически осмысленное описание пассивного транспорта. Тещщя ^опреДеляет кинетические характеристики мембраны (например, и и со), которые можно измерить на опыте. Основная идея тео - рт-состоит в том, что трактовка проницаемости мембран требует изучения неравновесных^ потоков вещества. Исходя из
этого, удается связать динамику транспорта со свойствами мембраны. На опыте установлена линейная зависимость потоков от обобщенных сил (градиентов химических и электрохимических потенциалов) для ряда пассивных искусственных и биологических мембран. Это означает близость к равновесию рассматриваемых сопряженных процессов.