ФИЗИКА ЖИЗНЕННЫХ ПРОЦЕССОВ

ТЕРМОДИНАМИЧЕСКАЯ МОДЕЛЬ НАТРИЕВОГО НАСОСА

Важной особенностью плазматических и возбудимых мем­бран, в частности, мембран аксонов нервных клеток, является активный транспорт ионов К+ и Na+. В нервных клетках, в эрит­роцитах и т. д. во внутриклеточном пространстве поддержи-

Вается значительно большая концентрация ионов К+ и значи­тельно меньшая концентрация ионов Na+, чем в окружающей среде. Принято говорить о «натриевом насосе», наличествующем в мембране, о химических процессах, которые, будучи прямо или косвенно сопряжены с диффузией, обеспечи­вают транспорт ионов щелочных ме­таллов в направлении возрастающей концентрации. Именно термодинами­ческое сопряжение ионных потоков с макроэргическими химическими реак­циями объясняет эту неравновесную ситуацию.

Рассмотрим транспорт веществаS через два мембранных элемента /и2 (рис. 3.2), облегченный неким пере^ носчиком С.

Всего имеется пять диффузионных потоков (/si, /s2, /s, /с, /cs) И два хи­мических потока (/хим и /хим) [16]. Функция диссипации имеет вид

Та = /51 Лц51 + 4 Лц5 + /S2 £ nS2 +

+ 'с ЛИс + 'cs A^cs + + 'й А (3-78) Имеем в стационарном состоянии

/с + /CS = о, /хим + /хим == о, /С = /хим = — /cs = — /хим» /si =/s + /cs = /s2 = /s-

Следовательно,

Ta = Jss( Ansi + Ans + Ans2) +

+ Jcs (A^cs - A. uc - Ahs + - (3-80)

Первый член (3.80) описывает внешний поток, второй член—■ циркуляцию. Однако, поскольку

- st2 = цС| - ЦС2 + Ц81 - fXS2 + HCS 2 - ^CS 1 = А^с + A^S - A^cs.

Второй член обращается в нуль и (3.80) можно переписать в виде

Та = Ац® = L (Дцд)2. (3.81)

2

/ \

Чк

Мембрана

Рис. 3.2. Облегченный транс­порт через два мембранных элемента.

(3.79)

Наличие циркуляции непосредственно влияет на коэффициент L. Покажем это. Рассмотрим внутренние потоки.

Реакции и химические потоки описываются уравнениями ft.

Сі - f - Si CSi, /xhm = ^iCISI — k-iCSi,

K.

(3.82)

C2 + S2 CS2, Л'им = k 1C2S2 — k-iCSr. k-i

Для транспорта переносчика через внутреннюю мембрану имеем /с = Рс(С,-С2), /cs==Pcs(CS,-CS2), (3.83)

Где Рс и Pes — коэффициенты проницаемости, измеряемые в с-1. С и CS— концентрации С и CS. Положим Рс = Pes = Р; тогда из (3.83) и (3.79) следует

С, (Ј, S, + + Р) - С2Р = Й_,С*, |

Где

С* = С, + CS, = С2 + CS2.

Решая эти уравнения, находим С и С2, J с, /cs.

PKSC* (S, - s2)

/CS = (*s + S,) (tfs + S2) + (2P/A,) [/Cs + '/2 (S, + S2)]' (3,85)

Где Кз~ k-i/ki. При Si^>Ks, S2 имеет место насыщение. Внешний поток равен

Е PKSC* (Sj - S2)

/s = Ps (S, - S2) + + S]) + Sz) + (P/Ai) {2K& + Sj + Sz) • (3.86)

Если Sj и S2 близки, то

Дц5 « РГ (S, - S2)/S, S = '/2 (S, + S2)

И

R PtfsC* •) S RT (S, —S,)

/s«^Ps + s [ ^4= ^ = (3.87)

\ ^ (tfs + S)(tfs + S + 2/>/*,)J RT S

Таким образом, коэффициент L в (3.81) состоит из двух членов, определяемых пассивным транспортом и циркуляцией. Поток течет от большего потенциала к меньшему, и наличие циркуля­ции влияет лишь на численную величину L, но не на ее знак, L> 0.

Рассмотрим «натриевый насос» как проблему облегченного транспорта. Можно считать установленным, что источником сво­бодной энергии, необходимой для создания потока в направле­нии, противоположном направлению падения концентрации, яв­
ляется АТФ. Опишем натриевый насос в терминах переносчи­ков, которые могут фосфорилироваться и дефосфорилироваться в различных областях мембраны

С + АТФ СФ +АДФ.

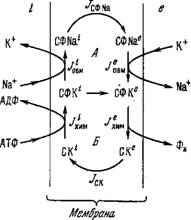
Рис. 3.3. Термодинамическая схема

Натриевого насоса. Индексы і и е относятся к внутренней и внешней сторонам мембраны. А — ионооб­менный цикл, В —химический цикл.

Предположим, что АТФ и АДФ реагируют лишь в том случае, когда они находятся на внут­ренней стороне мембраны. Фосфорилированный перенос­чик СФ дефосфорилируется в результате некоего конформа - ционного превращения

СфнДс + ф.

Предположим, что переносчик с — белок, имеющий большее химическое сродство к к+, а сф — белок, преимуществен­но связывающий Na+. Натрие­вый насос работает как систе­ма двух циклов, в которой один цикл движет другой (рис. 3.3). Первый цикл имеет ионообменный характер:

СФК + Na+ СФЫа + К+,

Второй — химический, т. е. происходят химические реакции фос - форилирования и дефосфорилирования. В стационарном состоянии

DCK* _ Ti, __n dCKe _ je, n

(3.88)

+ JCK — U, —J-f——/хим — JCK = U,

Dt

T. e.

: /Іим = /ск-

Для химического цикла получаем

DC<t>Nal dt

DC0Nae

— / C®Na — /обм»

Dt

/обм — Zc<i>Na = О,

Т. е.

(3.89)

DC<t>K

(3.90)

Dt

/ обм — / обм — / C®Na = /хнм — /обм — J СФК = 0.

Dt dC0Ke

= / СФК + /обм — 'хим — о,

Т. Є.

J СФК == J хим — /обм— /хим — /обм» (3.91)

Функция диссипации

То = JCK лцск + 4 Хнм + См<им + ;СФК Л^СФК +

+ 'сФМа ^М'СфМа + 'обм^обм + 'обм^обм' (3-92)

Где

== ^ск ^СК' А'ЦСФК= ^СФК ^СФК»

^СФЫа = ^MNa ^СФИа' ^чим ~ ^АТФ "+* РСК ~ РАДФ ~~ ^СФК' ^ким = ^СФК + ^н2о - ^ск - IV

•^оОм ^ ^СФК + '~lNa ~~ ^СФИа ~~

^ts е. г е е

•^обм — ^СФИа ^К ^Na ПЗФК*

Следовательно,

Т<У = 7хИМ <>АТФ + ^НгО - ^АДФ - ^ф) +

+ 'обм [К. - ^Na) - (К - «*)] = 'хим^хим + 'обм^обм* (3-93)

Коэффициент ионного обмена равен

. _ к1 [Nae]

(3.94)

Ке [Naf]

Феноменологические соотношения имеют вид

/обм — ^11-^обм + L\2

Хим» I хим - )

(3.95)

J хим = ^12-^обм "I"

Если Ln ф 0 и ^хим Ф 0, то, так как при /обм = 0 Х0бм = - ДЛпГ= Ll2 ^

Lu хим

Г отлично от единицы и Ln, L22 > 0. В случае эритроцитов

Таким образом, неравновесие поддерживается сопряжением двух циклов — ионообменного и химического.

Конечно, это всего лишь феноменологическая модель, пока­зывающая, что работа натриевого насоса в принципе возможна

При близости к равновесию, т. е. в условиях линейности. В дей­ствительности мы не располагаем надежными критериями бли­зости к равновесию активной мембраны и, тем более, доказа­тельствами именно такого сопряжения ионообменного и хими­ческого циклов.

Теория, изложенная в этом и предыдущих параграфах, спра­ведлива для стационарных процессов, протекающих вблизи равновесия. Она позволяет закономерно связать ряд фактов и существенно прояснить картину. В этом смысле линейная тер­модинамика действительно применима к рассмотрению ряда мембранных процессов. Однако необходимы и более общие подходы.

Дальнейшие подробности, относящиеся к неравновесной тер­модинамике мембран, содержатся в литературе (см. [4, 7, 8, 10, 13, 16—18]). Применение термодинамики сетей (см. стр. 79) к проблемам мембранного транспорта [17, 19] дает содержа­тельное феноменологическое описание соответствующих про­цессов.

Для выяснения сущности мембранного транспорта необхо­димо перейти от термодинамики к молекулярным кинетическим моделям. Такие модели могут строиться на различных уровнях, начиная с моделей, основанных на феноменологических допуще­ниях, и кончая моделями, имеющими надежное молекулярное обоснование. В настоящее время разрабатываются главным об­разом модели первого типа, так как наши знания о сложной надмолекулярной структуре мембран недостаточны.