ТЕОРИЯ СТАЦИОНАРНОГО МЫШЕЧНОГО СОКРАЩЕНИЯ
Из всего изложенного выше очевидно, что теоретический вывод уравнения Хилла должен основываться на рассмотрении внутреннего трения в мышце. Сама форма уравнения Хилла свидетельствует о том, что оно описывает вязкое течение и не содержит упругости. Представление о внутреннем трении естественно фигурирует в феноменологической теории Оплатки (см. стр. 238).
Соответствующая теория развита в работах [124] (см. также [ЮЗ]). В этих работах содержались ошибки, не сказывающиеся на конечных результатах, здесь эти ошибки исправлены.
Уравнение Хилла описывает стационарное укорочение мышцы. Получим это уравнение, исходя из скользящей модели с трением. Тянущее или толкающее усилие возникает в результате замыкания мостика и следующих за этим событий, состоящих в превращении химической энергии АТФ в энергию конформацион- ной перестройки белковой сократительной системы. Каждый мостик при замыкании развивает напряжение /о. Именно процесс замыкания и размыкания мостика и создает трение между перемещающимися нитями. Второй закои Ньютона для такой системы запишется в виде
MV = P'-P-BV, (5.42)
Где М — перемещаемая масса, Р — приложенное напряжение, Р' — развиваемое напряжение, BV — сила трения. В стационарных условиях V — 0. Представим Р в виде n0f, где п0 — максимальное возможное число работающих мостиков. Мостики работают асинхронно и при данной нагрузке в данный момент в укорочении мышцы участвует лишь некоторое эффективное число мостиков п = wn0, где w 1. Именно эти мостики, замыкаясь, развивают напряжение Р' = nf0 = wnaf0. Тем самым они уже ответственны за внутреннее трение, следовательно, В = = $wn0. Величина w зависит от Р, т. е. от /. Получаем для стационарного режима
Wfo—f — = 0, (5.43)
Откуда
Физическое предположение состоит в том, что w = njtiQ непосредственно зависит от силы /. Зависимость w от v возникает лишь вследствие зависимости силы от скорости. Очевидно, что это предположение независимо от закона сил (5.42), (5.43) и с ним согласуется. Определим вид функции w(f). При максимальной нагрузке Ро груз поддерживают все мостики, т. е. n(f0) = = n0w(f0) = n0 и w(f0)= 1. Соответственно согласно уравнению (5.44), при f = fo находим v = 0.
Напротив, при нулевой нагрузке работает минимальное число мостиков «(0) = nQw (0) = «mm и w(0) — «min/fio = г < 1. Макси - мальная скорость укорочения при f = 0 равна
Umax = /о/Э - (5.45)
Сделаем естественное предположение о том, что напряжение, развиваемое мышцей при изометрическом сокращении, или груз, поддерживаемый мышцей при изотоническом сокращении, линейно зависит от числа работающих мостиков, поскольку каждый из них развивает постоянное напряжение /.0. Следовательно,
P=n0f = (C + Dn)f0,
При / = /о имеем п = по и п0 — С -f Dn0, при / = 0 получаем п = rtmin 3= ГПо и С = —Drn0. Находим
W = n/n0 = r + (l-r)f/f0. (5.46)
Подставляя это выражение в (5.44), получаем уравнение Хилла в форме
F (т^7 f°+f)=J7^7(h-П. (5-47)
Следовательно, константы а и b имеют вид
« = - Г—ї°> (5-48)
B = T^7J> (5.49)
Опыт дает а » 0,25/о. Следовательно, г/(1 — г) 0,25 и г » 0,2. Из уравнения (5.47) следует, что при f — 0
= (5.50)
Таким образом, уравнение Хилла описывает пластическое течение вещества с внутренним трением, характеризуемым коэффициентом р. Следующая задача состоит в истолковании этого коэффициента, т. е. в переходе от феноменологического уравнения (5.47) к молекулярному.
Трение определяется всей совокупностью событий, происходящих при замыкании мостиков. Будем рассматривать как элементарный акт замыкание мостика, гидролиз одной молекулы АТФ, конформационное превращение мостика, производство им работы foL, где L — укорочение, производимое мостиком, и размыкание мостика. Обратный микроскопический акт приведет к синтезу одной молекулы АТФ из АДФ и Ф„ и к производству элементарной работы /0L над системой.
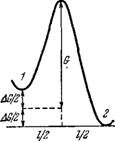
Воспользуемся теорией внутреннего трения жидкостей, развитой Эйрингом [125]. Изменение состояния системы можно представить кривой свободной энергии, показанной на рис. 5.21. Здесь 1 — состояние системы до замыкания мостика, 2 — после замыкания и всех последующих событий. Вся совокупность событий, объединенных в рассматриваемый элементарный акт, требует энергии активации. Это очевидно и непосредственно из сильной зависимости b от температуры (см. стр. 230). Приходящаяся на мостик внешняя сила, равная Р/п — ti0fln = fjw, препятствует переходу 1-+2 и способствует обратному переходу £->-/• Эта сила направлена вдоль мышечного волокна и, следо
вательно, под некоторым углом 0 к мостику (рис. 5.22). Тем самым на мостик действует сила fcosQ/w, которой отвечает энергия fl cos Q/w, где I — длина химической или хелатной связи, соединяющей выступ ТММ с активным центром актина.
(5.51)
-fw%9/w
Рис. 5.21. Кривая свободной энергии.
(5.52)
(5.53)
Скорость укорочения представится выражением
И = (v+ — v_) L = vL,
Где v+ и V - — числа элементарных актов перехода через актива - ционный барьер в единицу времени соответственно в направле-
Ниях 1-*2 и 2—(см. рис. 5.21). Расчет проводится применительно к одному мостику на основе микроскопической обратимости. Переходы 1-+2 означают укорочение, переходы 2 —* 1
F
\в
![]()
ТММ
Рис. 5.22. Схема работающего мостика.
— удлинение системы. Согласно теории Эйринга имеем (см. рис. 5.21)
Кът ( G+ Л Н т ( а_\
Где h — постоянная Планка,
G+ = G + fl cos 0/2w — >/2 ДG, G - = G — fl cos 0/2w + '/2 AG,
Fl cos в
2wkBr
■ AG
JW
V = Vj
K „Г = - f-2sh
Определим AG. Мы знаем, что при f = f0 скорость v = 0, т. е. v+ = v_. При этом w = 1. Получаем AG = /У cos 0, и (5.54) приобретает вид
KnT ґ G \ г /cosG / / \-| v = ехр ( - 2 sh [tj-jt (/о - -) J. (5.55)
Если
(6.56)
(F0-f/®)/cos9 <2/гБГ,
То
/ cos 6
(5.57)
Л
И
(5.58)
/ cos Є / й \ /. f \ IL cos в f О \ /, f \
Мы получили уравнение, аналогичное (5.44). Сравнивая уравнения (5.44) и (5.58), находим
(5.59)
(5.60)
Таким образом, |3, b, итах выражены через молекулярные параметры fo, I, cos 0, G.
Проведем численные оценки. Прежде всего необходимо убедиться в справедливости условия (5.56). Напряжение поддерживается в каждой половине саркомера. Для портняжной мышцы лягушки число мостиков N в объеме, равном произведению 1 см2 на длину половины саркомера 1,1 мкм, составляет 6,5-1012 [126]. Опыт дает Рц порядка 3 кГ/см2 = 3-Ю6 дин/см2. Один мостик создает силу f0 = P0/N = 4,6- Ю-7 дин. Примем длину связи 1 = 2 А и cos 0 (он меньше единицы) положим равным 0,5. Получаем Ы cos 0 = 4,6-Ю-15 эрг = 0,055-2kBT. Условие (5.56) выполнено.
Максимальная скорость укорочения портняжной мышцы лягушки при 0 °С VWx равна 1,33Л0/с, где А0 — начальная длина мышцы. В наших расчетах следует взять Ло = 1,1 мкм — половину длины саркомера. Следовательно, итах=1,5 мкм/с и b = 0,4-Ю-5 см/с. Элементарный шаг L имеет значение порядка 100 А. Подставляя в (5.61) значения f0L, cos 9, I, из экспериментально найденной величины итах (или b) находим G = = 14 ккал/моль. При повышении температуры на 10° (с 300 до 310 К) b должно возрастать в 2,14 раза. Опыт дает увеличение в 2,05 раза. Излагаемая теория хорошо объясняет температурную зависимость константы Ь.
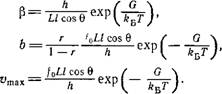
Ь
![]()
Из написанных уравнений следует
т. е. число одновременно работающих мостиков убывает с увеличением скорости v. Если v = О, то w — 1; если v = ymax = = b(l—r)/r, то w = wmln = г:
= Г = ь+1тах. (5.63)
Естественно, что изложенная теория дает результаты, эквивалентные теории Хаксли — Дещеревского (см. стр. 244). Сопоставим формулы. Из уравнений (5.38) и (5.48) следует
Подставляя в уравнение (5.34) стационарное значение т — = nv/Lk2 из (5.35), находим
П = п0 — + Р) п (5.65)
И при п = 0 получаем стационарное отношение п/по = w. Приравнивая его выражению (5.62), получаем
Kii^+^J^vy1 = b/(b + v). (5.66)
Из (5.60), (5.61), (5.64) и (5.66) находим
'.--МгМ-^т^-тч<5'67>
= (5.68)
Таким образом, можно выразить ki и k2 через молекулярные постоянные.
В изложенной теории трение возникает в результате замыкания и размыкания мостиков, так как эти процессы требуют энергии активации. Коэффициент трения, естественно, оказывается экспоненциально зависящим от температуры. В макроскопической теории молекулярная модель заменяется формальной моделью Хаксли — Дещеревского — мостик либо тянет, либо тормозит, хотя в действительности эти явления должны происходить одновременно. Преимущество излагаемой теории состоит в том, что она согласуется с принципом микроскопической обратимости и непосредственно выражает кинетические константы через молекулярные параметры L, cos0, G, fe. Тем самым объясняется температурная зависимость b и, как мы увидим, /0-
В изложенной теории предполагается, что мостики замыкаются независимо друг от друга. Насколько основательно это предположение? Нет ли здесь кооперативности в том смысле, что замыкание одного мостика влияет на замыкание других?
Идея о кооперативных, аллостерических свойствах актина и миозина высказывалась не раз.
Введем кооперативность в кинетику действия мостиков, предположив, что свободная энергия активации G сама является функцией числа работающих мостиков
G = G0 - wG' = G0 - [г + (1 - г) Ш G'. (5.69)
Характеристическое уравнение получается в виде (b имеет прежнее значение с G, замененным на G0)
(a + f)v = b ехр ехр [^f-■] (/о - П. (5.70)
При заметных значениях G'/ksT кривая v(f) оказывается выпуклой, а не вогнутой. Для согласования с опытом следует предположить, что G' < ЙбТ. В этом случае
(a + f)v*b[l+±j^-(a + f)-Јjr](f0-f), (5.71)
Т. е. кооперативность рассматриваемого типа вносит лишь незначительную поправку в уравнение Хилла, чго не представляет особого интереса.
Исходная идея изложенной теории состоит во влиянии внешней силы f на активационный процесс замыкания мостика и кон - формационного превращения белка. В свое время Полиссар предполагал экспоненциальную зависимость скорости некой неизвестной реакции, определяющей. сокращение, от внешней силы [127] (см. также [53]). Т. Хилл также вводил сходную экспоненциальную зависимость в своей теории фазового перехода в мышце [119]. Эти работы, однако, не давали возможности получить характеристическое уравнение и истолковать его константы. Нельзя считать изложенную теорию молекулярной в истинном смысле слова, так как она не дает реальной молекулярной модели работы мышцы. Построение молекулярной теории невозможно на современном уровне знаний о строении и взаимодействии мышечных сократительных и регуляторных белков и об их конформационных превращениях. Соответственно задачи исследования структуры и свойств этих белков, исследования их поведения в надмолекулярной мышечной системе особенно актуальны.
§ 5.7. ТЕОРИЯ ТЕРМОМЕХАНИЧЕСКИХ СВОЙСТВ МЫШЦЫ
В мышце, рассматриваемой как изолированная система, работа и тепло, выделяемые в элементарном акте, выражаются через уменьшение химической энергии
F0L + q0 Z Иг Ащ, (5.72)
Или, согласно закону сохранения энергии,
AE = TAS + fQL + Zv-i (5.73)
І
Причем TAS — qo - Изменение свободной энергии в рассмотренном элементарном акте составляет, как мы видели, fal cos 0 (см. стр. 249). Имеем
AG — AE — T AS = f0L + Е Ащ = fQl cos Є,
І
Откуда
Z » і
= - Г^ГВ ■ (5-74)
Максимальная сила f0 (и, следовательно, Р0) должна слабо расти с температурой как химический потенциал, т. е. пропорционально абсолютной температуре. Это согласуется с опытом.
Коэффициент полезного действия мышцы, согласно изложенной теории, равен
FoL + % L n« Д",
І
Если бы выполнялся закон сохранения энергии (5.73), то
1 - (l/L) cos Є '
1
QQ = T\S = - f0l cos9, п'
При cos0>O получаем ц' > 1, т. е. мы приходим к противоречию.
Как мы видели, проблема теплопродукции мышцы не проста (см. § 5.4). Она не может быть решена на основе столь простых соображений. Необходимо учесть запасание энергии и различные способы ее выделения. Соответствующая модельная теория предложена в работе [66]. Авторы этой работы считают, что энергия, освобождаемая при сокращении мышцы, должна слагаться из запасенной энергии, диссипируемой в центрах одного типа, и энергии, получаемой за счет распада АТФ в центрах другого типа. Теплота укорочения получается из диссипированной энергии. Предполагается, тем самым, что в двух типах центров действуют две различные актомиозиновые АТФ-азы. Факты, свидетельствующие в пользу такого предположения, состоят в следующем.
1. Центры Р и S, связывающие две молекулы АТФ (или АДФ), находятся в головках миозина [128]; в Р-центре лимитирующая стадия для Mg-зависимой АТФ-азы есть отделение
продукта, т. е. АДФ и Фн от миозина [129], в S-центре лимитирующая стадия есть гидролиз АТФ [55].
Актин активирует гидролиз АТФ в S-центре миозина.
Реакция Р-центра с АТФ необходима для сокращения.
Актин ускоряет освобождение продукта Р-центрами [129].
Энергия запасается в комплексе миозин — продукт. Факты, свидетельствующие об этом, приведены в работе [66]. И, наконец,
При контакте с актином в присутствии АТФ миозин не образует «комплекса окоченения» (rigor complex) с актином, т. е. миозин всегда нагружен продуктом и (или) субстратом.
Из этих шести положений и из предположений, приведенных на стр. 237, следует модель работы актомиозиновой АТФ-азы [66]:
Быстро -„ X
М + АТФ »- М —>• М + АДФ + Ф„, (I)
М + АТФ + FA М • (АТФ) • FA М + FA + АДФ + Ф„ + G, (II)
H ~
>-М + РА + АТФ + 02. (III)
Здесь М — миозин, М—комплекс миозин — продукт, т. е. комплекс М-АДФ-Фн, запасающий энергию, FA — F-актин, G\— свободная энергия, выделяющаяся при гидролизе одной молекулы АТФ, Gi — энергия, выделяемая М, т—время жизни запасенной энергии, /о, /ь І2 — реакционные потоки (скорости реакций).
Процесс (I) представляет реакции в Р-центре. Энергия, запасенная в комплексе М, выделяется в процессах (II) или (III). При исчерпании запасенной энергии комплекс М освобождает АДФ и Фн и затем вновь реагирует с АТФ и запасает энергию. Процессы (II) и (III) происходят при сокращении мышцы, в Р-центре. АТФ-аза катализирует гидролиз АТФ в S-центре, используя часть запасенной энергии, генерируемой в Р-центре. Это — своеобразная аллостерическая система.
Изменение свободной энергии в единицу времени в процессах (II) и (III) равно
- G = AGj + J2G2. (5.76)
В стационарном режиме
/0 = /1 + /2. (5.77)
Поток /1 выражает скорость гидролиза АТФ в S-центре. Он равен произведению числа комбинаций актин — миозин, создающих напряжение (числа работающих мостиков), на число оборотов реакции (II). Первый сомножитель пропорционален нагрузке
Р, второй линейно зависит от скорости укорочения V. Поэтому
H = P(KiV+ K^ = KiPV + K2P, (5.78)
Где К і и К.2 — константы. Перепишем (5.76) в виде
- G = /0G, - /2 (G, - G2) (5.79)
И предположим, что поток /2 линейно зависит от «сродства» А = Gj — G2 и нагрузки
—/2 = с, Л + с2Р. (5.80)
Наконец, пусть скорость укорочения линейно зависит от тех же величин
— V = c3A + с4Р. (5.81)
Из соотношений (5.77), (5.78), (5.80) и (5.81) следует уравнение Хилла в форме
Определим коэффициенты Cj. При Р — 0 имеем V = Fmax, А = Лт, /2 = /о и
= = (5.83)
Am Am
При P = P0 имеем l/=0, A = A0 и
С4=-Сз (5<84)
C2 = /e2+ r "(5.85)
Подставляя эти значения ct в (5.82), находим
(г> і ^ ir Л
Т. е. снова получаем уравнение Хилла, в котором
А =/„//Climax, b = Jq/KiPo - (5.87)
Одновременно имеем
А=-^А0 + ^-Ат. (5.88)
Го V шах
При выводе уравнения Хилла сократились все члены, содержавшие К2 и значения «сродства» А0 и Лт при нулевой и максимальной скорости укорочения. Сопоставление с теорией, изложенной в § 5.6, показывает, что в расчете на один мостик
, ь fal cos 0 г / G \ ,е 0„,
= Т-= —Г~ 7=7 ехР(~ Т^г ) (5-89>
И
Ki = (f0L)~l, (5.90)
Т. е. уравнение (5.78) имеет вид
H = + (5-91)
Считая, что энтальпия гидролиза АТФ примерно равна соответствующей свободной энергии [58], находим количество тепла, выделяемое в единицу времени
Q = - G-PV =/,G, + J2G2-PV. (5.92)
При Р = Р0 и V7 = 0 имеем
Qo = KibPo [G, - А0 (1 - Ki/KM - (5.93)
По определению скорость выделения тепла укорочения равна
Q-Q0 = aV. (5.94)
Из приведенных формул и уравнения Хилла получим
Где х = Р/Р0.
Для нахождения Лт и Л0 это сложное уравнение приравнивается выражению (5.27) а/Ро = 0,16 0,18 х при х = 0 и х = 0,5. В области 0 < х < 0,5 получается хорошее согласие с результатами Хилла. То же относится к полной скорости выделения энергии. Эффективность мышцы (как функции х) , , ч PV Ь х (1-х)
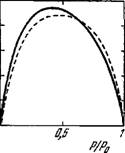
Вычисленная на основании излагаемой теории, хорошо согласуется с найденной Хиллом (рис. 5 23).
Из экспериментальных данных следует, чго Gu т. е. изменение свободной энергии при гидролизе одной молекулы АТФ есть величина порядка 10 ккал/моль.
Скорость выделения энергии
Е = — G = J0G| /2G2. За время At выделяется энергия
At At
(5.79)
AE = ^Gl (KiPV + K2P) dt + J J2G2 dt =
At
At
At
= G,/Ci J PV dt+ G^Kn J Pdt + J /2G2 dt & 0 0 0
А работы + А тепла. (5.97)
Процессу (III) отвечает последний интеграл в правой части. Тепло выделяется как в процессе (II), так и в (III). При Р == 0 остается лишь последний член — диссипирует запасенная энергия. При изометрическом сокращении j| V = 0, т. е. за выделенное тепло 1 W ответственны два интеграла. Чем g больше скорость укорочения, тем больше энергии превращается в тепло и тем меньше вклад процесса (II). Не имеет смысла разделять Ц.^ теплоту на теплоту укорочения и ^ теплоту поддержания. д
Химические изменения за то же время выражаются формулой
— АГАТФ1 ~К\А работы + Рис. 5.23. Зависимость эффек-
1 ' 1 г тивности мышцы от нагрузки.
S
, Сплошная линия получена теорети-
Р dt -)- \ j dt (5.98) чески [66]. пунктирная найдена на
TOC \o "1-3" \h \z о о
Где / « 0 при At < т, так как предполагается, что энергия запасена в комплексе М до начала сокращения. Этим изменениям соответствует энергия
At At
G, (- А АТФ) = alKlА работы + QXK2 j Р dt + G, J / dt. (5.99)
Кажущееся нарушение баланса между выделившимся теплом и химическим превращением определяется тем, что
At At
J J2G2dt>G^ jdt.
9 М, В. Волькенштейн
Разность этих двух интегралов равна заранее запасенной энергии. Время жизни запасенной энергии
_ запасенная энергия
Т— Та '
Так как /2<32 есть скорость освобождения запасенной энергии. Численные оценки дают 0,2 c<t<0,9 с в интервале Vmai ^ > V 3-s 0, т. е. 0 < Р < Р0.
В опытах, проводимых за время, меньшее 0,2 с, / «* 0 н не наблюдается соответствия между химическим превращением и выделившимся теплом.
Теория, предложенная в работе [66], хорошо объясняет основные факты, относящиеся к теплопродукции мышцы. Однако эта теория основана на модели, хотя и хорошо аргументированной, но все же содержащей ряд постулативных положений. Подлинный молекулярный механизм процесса остается неизвестным. Путь к его познанию идет через детальное изучение строения и свойств мышечных белков.