ФИЗИКА ЖИЗНЕННЫХ ПРОЦЕССОВ

РАСПРОСТРАНЕНИЕ НЕРВНОГО ИМПУЛЬСА

Прежде чем исследовать процессы, определяющие генерацию нервного импульса, рассмотрим его распространение. Известны более простые электрохимические процессы, весьма сходные с движением нервного импульса. Их изучение весьма поучи­тельно. В частности, такой процесс происходит при погружении железной проволоки в концентрированную азотную кислоту. Железо при этом не растворяется, так как на его поверхности образуется пассивирующая пленка окисла. Если разрушить пленку в каком-нибудь месте, то идет бурная реакция раство­рения. Этот процесс распространяется вдоль проволоки, дви­жется фронт активации, за которым следует фронт репассива - ции. Оствальд первым обратил внимание на сходство этого процесса с распространением возбуждения по аксону [25]. Далее явление было подробно изучено Лилли [26], именем которого была названа эта модель. Действительно, процесс характери­зуется пороговым значением тока, наличием рефрактерности и т. д. Электрохимия явления была изучена Бонхеффером и Феттером (см. [27]), Бонхеффер начал соответствующие тео­ретические исследования [28, 29] (см. также работы Ямагивы, посвященные этим явлениям в сложных геометрических струк­турах из неоднородных проволок [30], работу Смолянинова [31] и др.).

Модель Лилли была исследована теоретически на основе рассмотрения физико-химических процессов [32—35].

Процесс активации начинается при пороговом значении по­тенциала, ниже которого окисная пленка устойчива. Разруше­ние пленки происходит неравномерно, площадь пассивных уча­стков сокращается, так как растворение железа способствует дальнейшей активации поверхности. Далее возникает репасси- вация, так как накапливающаяся азотистая кислота усиливает окислительную активность азотной кислоты. Потенциал сни­жается и наконец становится ниже порогового. Распространение импульса активации объясняется действием локальных токов, текущих из зоны активного растворения железа и запускающих механизм активации. Теория раскрыла аналогию модели Лилли и распространения нервного импульса. Получено количествен­ное согласие с опытом (см. [36]).

Другая электрохимическая модель, проявляющая свойство возбудимости — мембранный осциллятор Теорелла [37]. Система состоит из двух ячеек, заполненных электролитом разной кон­центрации и разделенных мембраной из пористого стекла, со­держащей связанные отрицательные заряды. С помощью внеш­них электродов пропускается постоянный ток, создающий мем­бранную разность потенциалов. При больших токах в системе возникают периодические колебания мембранного потенциала и сдвинутые по фазе колебания уровня жидкости. Это—нели­нейные электрокинетические явления, которые рассматриваются в гл. 8. Здесь мы укажем, что на основе модели Теорелла была построена протяженная система, в которой волна возбуждения распространялась вдоль мембраны [38]. Теория распространения возбуждения в системе Теорелла развита в работах [39] (см. также [35]).

Электрохимические модели не адекватны мембранной си­стеме аксона. Однако решение соответствующих задач матема­тической физики имеет единую основу. Поэтому теория распро­странения нервного возбуждения действительно оказывается во многом подобной теории распространения возбуждения в ука­занных моделях (см. [40]).

Нервное возбуждение можно разбить на ряд стадий. Процесс начинается с локальной генерации потенциала действия. Далее импульс распространяется по нервным волокнам — аксонам — и по синцитиям, т. е. по системам, состоящим из многих воло­кон, причем импульс может переходить с одного волокна на другое. Синцитиальное строение свойственно гладким мышцам, выстилающим полые органы животных. Нервное возбуждение переходит от одного нейрона к другому посредством синапти - ческой передачи, природа которой представляет особую проблему.

Прежде чем рассмотреть генерацию импульса, определяемую физико-химическими процессами в активной мембране, обра­тимся к физической трактовке распространения импульса. Эта задача в некоторых отношениях имеет более простой и опреде­ленный характер. Она исследовалась в ряде теоретических ра­бот, основанных на различных моделях возбуждения. Укажем, в частности, на модель Рашевского [41], в которой вводились два параметра. Эта модель позволяла описать распространение возбуждения, исходя из того, что каждая область нервного волокна после достижения порога генерирует постоянный про­дольный ток. Сходная модель принадлежит Раштону [42], рас­смотревшему эквивалентную электрическую схему мембраны. Вайнберг показал, что для определения скорости распростране­ния импульса нет надобности детально рассматривать его генерацию [43].

В работах Насонова развита так называемая градуальная теория нервного импульса, согласно которой по мере увеличения интенсивности раздражения постепенно нарастает электриче­ская реакция [44] (см. также [45]). Существенным результатом этих работ было предсказание возможности существования двух бегущих импульсов — устойчивого и неустойчивого. Необходимо также указать на модельную теорию, предложенную в работах [46—49], в которых движущийся импульс представлялся генера­тором э. д. е., включаемым при достижении порогового потен­циала, причем вводилось входное сопротивление невозбужден­ной области и внутреннее сопротивление генератора. Были полу­чены важные качественные результаты. Скорость распростра­нения импульса удалось вычислить путем введения еще одного параметра [41].

Важное значение имели работы Ходжкина и Хаксли [3, 50]. Они решали всю проблему теоретического расчета как формы потенциала действия, так и скорости распространения импульса в аксоне.

Исходное уравнение для мембранного тока, возникающего в однородном участке в ответ на изменение потенциала, можно написать в виде

/т = С §- + /„ (4.7)

Где <р — разность потенциалов между обеими сторонами мем­браны аксона, С-^-— емкостный ток, связанный с изменением плотности ионов на наружной и внутренней поверхностях

Гл. 4. нервный импульс

Мембраны, ІІ — нонный ток, определяемый движением через мембрану заряженных частиц. В аксоне кальмара U состоит из токов ионов Na+ и К+ (/иа и /к) и тока утечки /.

Ходжкин и Хаксли показали экспериментально, что эти нонные токи линейно зависят от соответствующих разностей потенциалов

/Na = ^Na (ф ~ <Рыа)

Н т. д. Теория Ходжкина н Хакслн основывается на раздельном рассмотрении калиевого и натриевого компонентов, ионного тока [51]. Для их измерения применялся метод фиксации напряже­ния (voltage clamp). Воспользуемся моделью, показанной на рнс. СТО. Замыкая мембрану металлической проволокой, можно резко уменьшить мембранный потенциал до нуля. Конденса­тор С разряжается и после этого ток создается лишь ионами, проходящими через /?Na и При резкой деполяризации мем­браны до некоторого значения потенциала, лежащего между 20 и 110 мВ, общий ионный ток сначала представляет собой входной ток Na+ по градиенту концентрации, спустя примерно 1 мс этот ток уменьшается н возникает выходной ток К+. Если общая разность потенциалов равна фиа, наблюдается только калиевый ток. При ф > фиа натриевый ток направлен наружу. Разделение тока на компоненты можно провести, изменяя кон­центрации ионов Na+ и К+. На рис. 4.13 показаны наблюдаемые кривые l(t) [3]. Если аксон погружен в морскую воду, полный ток / = /Na + ^к изображается кривой 1. При замене Na+ холи - ном наблюдается чистый калиевый ток (кривая 2). Разность этих двух кривых 3=1— 2 дает /иа - При быстром изменении потенциала внутри волокна на +56 мВ («короткое замыкание» мембраны) натриевая проводимость gNa сначала быстро растет от нуля до 25-Ю-3 Ом-'-см-2, а затем убывает (рис. 4.14) [3]. Калиевая проводимость медленно возрастает, следуя S-образ - ной кривой, и через 5—6 мс достигает постоянного уровня. При реполяризации мембраны gNa убывает значительно быстрее, чем gк - При различных смещениях мембранного потенциала наблюдается закономерное изменение кривых gNa(0 и ^к СО- Калиевая и натриевая проводимости мембраны аксона суще­ственным образом зависят от присутствия ионов Са++ (см. §4.3).

178

Удовлетворительное описание наблюдаемых изменений уда­лось получить при несколько искусственных предположениях [48, 50, 51]. Ходжкин и Хаксли исходили из того, что К+ может проходить через мембрану лишь в том случае, если к опцеде - лїятому ее участку ТГОД ВЛИЯНТГИЙ ' электрического поля подой­дут четыре однозарядные-чаетицы. Проводимость для К+ равна
где — максимальная проводимость, п < 1—вероятность под­хода предполагаемой частицы. Кинетическое уравнение для п имеет вид

■Л = ап (І — п) — р„/г, (4.9)

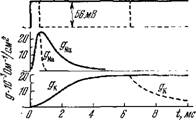
Рис. 4.14. Изменение gNa и gK при деполяризации мембраны на 56 мБ.

Сплошные линии — проводимость при длительной деполяризации, пунктир — проводимость при реполяризации мем­браны через 0,6 и 6,3 мс.

Где константы скорости ап и р„ при постоянной концентрации ионов Са++ зависят только от мембранного потенциала. При возрастании положительного потенциала внутри волокна ап увеличивается, р„— уменьшается.

Внутренний потенциал

5ВмВ

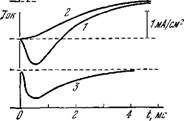
Рис. 4.13. Разделение мембран­ного тока / на калиевый и на­триевой компоненты [3].

1 — '='Na+'K> натрий заменен хо - лином, / = //£, 3 — 1—2, / = Отклоне­ние вверх—выходящий ток.

Следующее предположение состоит в том, что натриевый канал открывается, если одновременно в данный участок попа­дают три активирующих частицы и удаляется одна блокирую­щая. Обозначив вероятность прихода активирующей ча'стицы через т и вероятность удаления блокирующей частицы через Л,

Получаем - .

= (4.10)

Для тик записываются уравнения, аналогичные (4.9):

M = am(l — т) — pm/n, (4.11)

H = ah{\-h)-^h. (4.12)

Когда внутренняя часть аксона становится положительной, ат и p/j возрастают, рт и an убывают.

Щщ.-.,фиксироваHHQM.--HапрЯжении /всЕ аир постоянны; сле­довательно, n, т и h экспоненциально зависят от времени.

180 гл. 4. НЕРВНЫЙ импульс

Расчет кривых зависимости gK и gNa от t и ф по формулам (4.8)—(4.12) дает прекрасное согласие с опытом.

Полный мембранный ток дается выражением (ср. (4.7))

1 = С1и + (ф - Фк) ^к"4 + (ф - Фыа) + (Ф - Фу) ёу, (4.13)

Где С — емкость мембраны на единицу площади.

Первый член (4.13)—емкостный ток, gy — проводимость для ионов С1~ и других ионов, отвечающая утечке. Вызовем по - ,„тенциал действия коротким

Импульсом. После окончания и е /~Ч раздражения и радиальный и

3)\ J продольный токи в данном

Л^ У F^S _ участке аксона равны нулю.

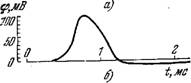
T, Mc Следовательно, 1 = 0 для t > 0. Зависимость ф(0 на­ходится из (4.13), если взять в качестве граничного условия начальное значение ф. Теория дает хорошее согласие с опы­том (рис. 4.15) [3]. Рис. 4.15. Распространяющиеся по - Рассмотрим некоторый уча-

Тенциалы действия. сток акСона длиною I. Радиус

А_теория, б-опыт, (аксон кальмара при аксоплазмы равен а, ЄЄ СО-

Противление Ra. В стационар­ном состоянии ток, втекающий в рассматриваемый участок, ра­вен нулю. Имеем

It а

Где / дается уравнением (4.13). В левой части (4.14) фигури­рует дивергенция продольного тока, справа — мембранный ток. Если импульс распространяется со скоростью v, то справедливо волновое уравнение

И из (4.13) — (4.15) следует уравнение Ходжкина — Хаксли

Ж'=С ^ + (Ч> ■" Фк)+ (Ф " Ф, а)g^nfh +

+ (ф <Py)gy (4.16)

Численное решение (4.16), отвечающее конечным значениям ф, дает скорость и, хорошо совпадающую с опытной. Так, для аксона кальмара скорость, вычисленная с помощью опытных
значений a, Ra, С, <pK, cpNa, gK, gNa, gY равна 18,8 м/с. Экспери­мент дает 21,2 м/с. При этом значении v потенциал после окон­чания спайка возвращается к уровню покоя.

Теория Ходжкина — Хаксли привела к несомненному успеху. Однако она чрезмерно сложна. В теории фигурируют четыре параметра: <p, п, т, h из которых лишь <р имеет прямой физи­ческий смысл и может быть измерен. Приведенное толкование величин п, т, h имеет лишь условный характер.

В ходе дальнейших исследований удалось разделить и упро­стить задачу. Оказывается, что при расчете скорости распро­странения импульса можно отвлечься от его точной формы и рассмотреть движение импульса по электрическому кабелю, образуемому мембраной аксона и характеризуемому опреде­ленными значениями сопротивления и емкости. Индуктивность волокна существенной роли не играет [52]. Соответствующие подходы реализованы, в частности, в работах Компанейца [53, 54]. Предполагается, что при распространении импульса можно различать четыре фазы. Во-первых, разность потенциалов воз­растает от своего значения в покое <р0 до порогового значе­ния ф'. Во-вторых, она возрастает с <р' до ф* — до потенциала действия. Затем система возвращается к исходному потенциа­лу фо, и, наконец, переходит в рефрактерное состояние. Ско­рость распространения одиночного импульса определяется лишь первыми двумя фазами, в которых потенциал нарастает. Задавшись прямоугольным начальным импульсом тока и учи­тывая значения емкости и сопротивления на единицу длины аксона и его радиус, удается вычислить скорость распростра­нения как в немиелинизированном, так и в миелинизированном аксоне в разумном согласии с опытом. Полученные зависимо­сти скорости от названных параметров следуют и непосред­ственно из соображений размерности.

Дальнейшее развитие теории распространения импульса проведено в работах Маркина, Чизмаджева и др. [35, 39, 55— 57, 98, 99].

Распространение возбуждения по немиелинизированному однородному волокну описывается общим уравнением

Дф (х, t) 1 д\ (х, t) I...

Dt ~~ RC дх2 С'

Где ф — потенциал мембраны, отсчитываемый от потенциала по­коя, R — сумма внешнего и внутреннего сопротивлений на еди­ницу длины волокна, С — емкость, отнесенная к единице длины волокна, / — ионный ток, текущий через мембрану (также от­несенный к единице длины волокна). / > 0, если ток течет наружу.

Ионный ток— знакопеременная величина. Сразу по дости­жении порога он течет внутрь волокна, а спустя некоторое вре­мя меняет направление и течет наружу. Действительно, потен­циал мембраны после прохождения импульса возвращается к исходному значению. Соответственно делается наиболее про­стое предположение о токе, текущем через мембрану при ее возбуждении. Ионный ток аппроксимируется двумя прямоуголь­ными «столиками» (рис. 4.16). Импульс тока, направленный внутрь, имеет модуль /і и продолжительность ті, следующий за

Ним импульс /2 направлен на­ружу и имеет -продолжитель­ность т2. В работах [53, 54] в сущности рассматривается лишь импульс /ь Кроме того, учитывается утечка тока через пассивную проводимость мем­браны, дающая вклад <p jrm, где гт—сопротивление мем­браны единицы длины аксона в состоянии покоя.

Таким образом, проблема четко сформулирована как задача математической физи­ки. Ищем волновое решение уравнения (ср. стр. 180). Вводим координату I = х — vt, где v — скорость распространения им­пульса. Уравнение (4.17) переписывается в виде

+ = (4.18)

При условии ф(оо) = 0 и условии конечности ф при g—>•—ОО решения уравнения (4.18) записывают следующим образом: В области g > О

Ф ® = 2В (А + В) & + h ехР І" у (ті + тг) (А + В)) —

-(/і + /2)ехр[-ит,(Л + В)]}ехр[-(Л + В)|] (4.19)

(здесь и далее Л = В = ('/4irW + R/rm)'h)-

В области — fti^g^O

<Р ® = 2В(А + В) & ехр и (Т) + Тг) (Л + ~

- (h + /2) ехр [- VX, (А + В)]} ехр [- (А + В) а -

Ток, мА

Рис. 4.16. Аппроксимация ионного тока при возбуждении мембраны.

~ 2 В {В-А) ехР - Ш+ Uh. (4.20)

В области — у(Т) + Tg^g^oT)

V (£) = 2 В (В - A) Wi + ^ еХР - - /і) еХР l(fl - А) а +

+ 2В(А + В) ехР I - у (Т1 + т2) (Л + В) - (Л + В) а - rmj2. (4.21)

В области | ^ — у (Т) + ^г)

<Р (S) = 2 в (В - A) М + ехР [ут> ~ ~

- І2 ехр [v (т, + т2) (В - Л)] - /,} ехр [(В - А) I]. (4.22)

Приравнивая напряжение ф(0) в точке, где включен ток, по­рогу возбуждения <р', получаем уравнение для скорости v

2В (/+ В) {/і + і2 ехр [- у (т, + т2) (Л + В)] -

- (/і + /2) ехр [- ОТ! (Л + В)]} = ф'. (4.23)

Надо еще учесть, что при возбуждении заряд, протекающий в одном направлении, равен заряду, протекающему в другом на­правлении

Мі = /2*2- (4.24)

Уравнение (4.23) относительно у имеет два решения. На рис. 4.17 показаны кривые ф'(и) для трех значений проводимости утеч­ки gy. Принятые параметры (аксон кальмара): /, = 63 мкА, /2 = 40 мкА, ті = 0,35 мс, т2 = 0,55 мс, С = 0,157 мкФ/см, удельное сопротивление аксоплазмы р = 50 Ом • см, диаметр аксона d — 0,05 см, ф'= 18,5 мВ. Прямая ф'= 18,5 мВ пере­секает кривую ф'(у) в двух точках при достаточно малых зна­чениях gy.

Считая экспоненты близкими к единице, находим большую (уі) и меньшую (у2) скорости

= j\/((p'RC2) - 2l(rmRC) 1 (ji/(<f'RC2) -1 /(rmRC))4> ' к ■ '

Пренебрегая проводимостью мембраны в состоянии покоя, т. е. положив Гт -> оо, находим

Что совпадает с формулой Компанейца. Зависимость v{(d) сле^ дует из того, что /1 ~ d, R ~ d~2, С ~ d. Получаем у~4Ч% чур рогласуется с опытом.

Решение устойчиво, v2 — неустойчиво. Пусть скорость V\ возросла на некоторую малую величину. Тогда, как видно из рис. 4.17, потенциал в средней точке импульса уменьшится и окажется ниже порогового значения <р'. В результате импульс замедлится. Если же Ui уменьшится, то потенциал в передней точке будет превосходить порог и возбуждение начнет распро­страняться быстрее. Для v2 справедливы обратные соотношения.

При расчете по фор­муле (4.27-) при указан­ных значениях парамет­ров получаем = 23 м/с; при расчете по фор­муле (4.25) с учетом опытного значения гт = = 6,37 • 103 Ом • см — Di = 21,5 м/с. Опыт дает Ui=21,2 м/с. Совпаде­ние превосходное (даль­нейшие подробности см. в цитированных работах).

Таким образом, тео­рия показывает, что ско­рость распространения импульса определяется электрическими и геометрическими параметрами аксона и пра­вильный результат получается практически независимо от фор­мы исходного импульса. Для решения задачи о скорости рас­пространения нет надобности пользоваться какими-либо спе­циальными предположениями.

На тех же основаниях решается ряд других задач, относя­щихся к распространению возбуждения. Решение для волокна переменного сечения показывает, что по мере приближения к расширению волокна скорость импульса падает, а затем, по­сле прохождения границы, асимптотически возрастает до по­стоянной величины. При обратном движении скорость возра­стает по мере приближения к сужению, а затем падает допре­дельного значения. При определенном соотношении радиусов узкой и широкой части волокна происходит блокировка импуль­са в расширяющемся участке [35, 48].

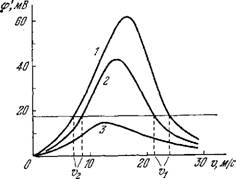
Рис. 4.17. Скорость распространения импульса при различных проводимостях утечки gy:

L-gy=--0-. 2-gy = l Ом-1 . см-2 ; =

= 5,74 Ом-1 • см"2.

Распространение одиночного возбуждения в ветвящемся во­локне [35, 59] своеобразно в том смысле, что в случае разно­временного подхода двух импульсов к точке ветвления происхо­дит их синхронизация. При определенных условиях импульсы блокируются.

Развита теория взаимодействия нервных волокон в пучках и стволах [35, 60]. При возбуждении одного из волокон в сосед­них распространяются волны наведенного потенциала, изменя­ющие их возбудимость. Вероятность передачи возбуждения от одного волокна к другим оказывается малой, но при возбуж­дении сразу большого числа волокон возбуждение может пе­рейти на соседние невозбужденные волокна тем легче, чем больше его радиус и чем меньше объем межклеточной жидко­сти. Вероятность такой передачи наиболее высока в неоднород­ных участках нервных стволов [35, 61]. Дана теория коллек­тивного возбуждения одновременно раздражаемых параллель­ных волокон.

На тех же основаниях рассмотрено распространение воз­буждения в синцитиях — в предельных случаях редкой и густой сети. Второй случай рассматривается в терминах сплошной возбудимой среды [35, 62]. Показано, что в таких средах воз­можны сложные режимы возбуждения типа ревербераторов (см. § 8.10).

Кратко перечисленные здесь результаты теоретического рас­смотрения находятся в качественном согласии с опытными дан­ными.

Таким образом, физико-математическая теория распростра­нения нервного возбуждения не только объясняет обширную совокупность фактов, но позволяет выйти на подступы к иссле­дованию нервной системы в целом. Биофизика встречается здесь с рядом задач, еще далеких от решения. Эти направления ис­следования ведут физику к познанию еще совершенно загадоч­ных явлений, относящихся к высшей нервной деятельности.