ФИЗИКА ЖИЗНЕННЫХ ПРОЦЕССОВ

КИНЕТИЧЕСКИЕ СВОЙСТВА МЫШЦЫ

Кинетическое поведение мышцы в целом представляет осо­бый интерес. Стационарное сокращение, для которого справед­ливы уравнение Хилла и теория, изложенная в § 5.7, есть лишь частный случай.

Простейшее кинетическое уравнение, описывающее прибли­жение к стационарному состоянию, можно представить в виде

/г = т-1(л0ау — га), (5.129)

Где га — число работающих мостиков, т — некоторое время ре­лаксации. Подставляя в (5.129) значение w — доли работаю­щих мостиков (см. (5.62)), имеем

Решение (5.129) записывается следующим образом:

N(t) = n (0) ехр (— t/t) + raoffi) (1 — ехр (— //т)), (5.131)

Где п{0) — значение га при t = 0. Уравнение (5.130) справедливо лишь в области физиологических длин мышцы. В общем случае уравнение (5.130) не линейно, так как п0, т и v зависят от длины саркомера и, значит, от времени. Время установления стационарного состояния т можно найти с помощью уравнений Дещеревского (5.34) и (5.35), положив в них т= 0. Получаем при этом уравнение (5.65), т. е. уравнение (5.130) со значением

-c = {kl + [v(kl +k2)/Lk2]}~[; (5.132)

Воспользовавшись затем (5.67) и (5.68), находим

Эти упрощенные представления совершенно недостаточны. Урав- ненйе (5.129) написано на основе общих соображений, а не изу­чения нестационарной кинетики мышечного сокращения. В не­стационарном переходном режиме могут наблюдаться колеба­ния, как правило, затухающие. Это реализуется, в частности, в опытах по быстрому отпуску (quick release)—изометрически со­кращенная мышца освобождается и испытывает быстрое изото­
ническое сокращение. Такого рода колебания — быстро и мед­ленно затухающие — наблюдались в ряде работ [54, 134—136]. На рис. 5.25 показана зависимость P(t) для портняжной мышцы лягушки после быстрого отпуска [136].

Каково происхождение этих колебаний? В цитируемой выше работе мышца рассматривается как однородный стержень с рав­номерно распределенными массой М и жесткостью S. Укороче­ние вызывает появление продольной волны, которая распростра­няется вдоль мышцы и отражается на ее концах. Наименьшая резонансная частота такой системы vr = (1 /2я) д/S/M. Измерен­ные частоты затухающих колебаний оказываются несколько

Р

Бме

Рис. 5.25. График Р (t) при быстром отпуске [136].

О

Меньше вычисленных и имеют порядок величины килогерц для мышц длиною в несколько сантиметров.

Возникновение колебаний может определяться нелинейностью нестационарных кинетических уравнений, не содержащих упру­гости в явном виде. В этом случае возможность колебаний обусловлена кинетикой замыкания и размыкания мостиков. Та­кой точки зрения придерживался Дещеревский [117, 134]. Сход­ные представления развиваются в работах Подольского и Но - лана [137—139]. Предполагается, что скорость замыкания мо­стика настолько велика, что нелинейные явления при быстром отпуске определяются лишь числом замкнутых мостиков, но не событиями внутри отдельного мостика. В этой модели почти все мостики замыкаются каждый раз, когда они возвращаются к началу своего цикла. Напряжение в мышце и расщепление АТФ изменяются надлежащим образом при изменении скорости уко­рочения, так что при больших скоростях много мостиков оказы­ваются тормозящими (см. также [212]).

Альтернативная модель предложена А. Хаксли и Симмонсом [135, 211]. Предполагается, что сам мостик является вязкоупру - гой системой. Напряжение, генерируемое замкнутым мостиком,
может изменяться шаг за шагом, в зависимости от угла, под которым «головка» ТММ S1 располагается относительно актина, а также от степени растяжения S2. Переходы между этими ша­гами, происходящими с большой, но конечной скоростью, влияют на быстрый нестационарный ответ мышцы, и таким образом можно детально объяснить природу быстрого отпуска. Замыка­ние и размыкание мостика в этой модели происходят сравни­тельно медленно и лимитируют скорость укорочения при уме­ренных нагрузках. В каждый данный момент число работающих мостиков убывает с ростом скорости v (ср. стр. 250). Таким образом, причина колебаний при быстром отпуске состоит в упругой деформации самого мостика.

Несмотря на то, что пока нет возможности непосредственно измерить число одновременно работающих мостиков и скорости их замыкания и размыкания, следует отдать предпочтение вто­рой модели как более естественной (см. [212]).

Включение упругих элементов в модельное описание мышцы проводилось и в других работах, в частности, в работах, посвя­щенных исследованию поведения мышцы, подвергнутой дейст­вию периодической нагрузки (см., например, [140, 141]).

Все предшествующее изложение относилось к поперечно-по­лосатым скелетным мышцам позвоночных. Большой интерес для физики и биологии представляют летательные мышцы насеко­мых (ЛМН) и близкие к этим мышцам по функции и строению тимпанальные мышцы цикад. Они были предметом присталь­ного внимания ряда исследователей, прежде всего Прингла [142, 143]. Эти мышцы способны к быстрым периодическим со­кращениям с частотой порядка 100 Гц. В структурном отноше­нии ЛМН весьма сходны с поперечно-полосатым и мышцами позвоночных. Они также обладают поперечной полосатостью и образуют в сечении гексагональную сетку из тонких и толстых нитей — из актина и миозина. Экспериментальные данные, полу­ченные в биохимических, электронно-микроскопических и меха­нических исследованиях, свидетельствуют о применимости к ЛМН скользящей модели с мостиками актин — миозин.

Для понимания природы быстрых колебаний ЛМН нужио учесть два обстоятельства.

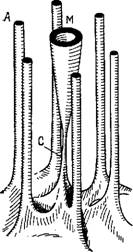
Во-первых, такие быстрые колебания требуют наличия не­посредственно функционирующего упругого элемента. Микро­скопия показывает, что в отличие от мышцы позвоночных в ЛМН наблюдается прямая вязкоупругая связь между миозиио - выми нитями и Z-мембранами, осуществляемая элементом С. На рис. 5.26 показано установленное на опыте расположение акти - новых (А) и миозиновых (М) нитей, элемента С и Z-мембраны [143, 144]. По-видимому, элемент С способен испытывать боля­щие упругие деформации (см. также [213]).

Во-вторых, установлена несинхронность колебаниий ЛМН и колебаний потенциала, который на них подается. Так, у мухи частота потенциала, подаваемого на ЛМН, равна 3 Гц, а ча­стота колебаний крыльев достигает 120 Гц. Следовательно, не происходит активации мышцы в каждом периоде колебаний. Характерно, что ЛМН содержат мало саркоплазматического ретикулума. Соответственно трудно предположить, что быстрое

Возрастание и падение напряжения при колебаниях связано с приходом и уходом ионов Са++.

Таким образом, колебания ЛМН имеют характер автоколебаний. На рис. 5.27 показан типичный

0.8

% ь-

*

4 8

Растяжение, %

I

12

Рис. 5.27. Цикл автоколебаний летательной мышцы жука-носо­рога II43].

Цикл автоколебаний летательной мышцы жука-носорога — за­висимость напряжения от деформации [143]. Изменения напря­жения и деформации происходят не в фазе, причем первое от­стает от второго — цикл обходится против часовой стрелки.

Как известно, автоколебания возникают в нелинейных си­стемах с трением за счет сил, зависящих от состояния движения самой системы, причем размах этих колебаний определяется свойствами системы, а не начальными условиями. В простейшем случае уравнение движения автоколебательной системы с одной степенью свободы имеет вид

X + ®2х + %(х) X = 0,

Ґ г \

Рис. 5.26. Схема микроско­пического строения лета­тельной мышцы насекомого.

Где х(х) — нелинейная функция от смещения х [145]. Подробное рассмотрение автоколебаний в биологических системах дано в гл. 8. Очевидно, что автоколебания ЛМН возбуждаются при на­личии обратной связи между деформацией и напряжением. Взаи­
моотношение напряжения и деформации изменяется в зависимо­сти от состояния активности системы. По-видимому, в ЛМН имеется элемент-преобразователь, реагирующий на механиче­ские события и контролирующий состояние сократительной си­стемы. Этот элемент локализован именно в миофибриллах, что доказывается наличием автоколебаний и у препаратов ЛМН, от­мытых глицерином. Прингл считает, что наличие элемента - преобразователя проявляется в увеличении числа возможных мостиков при возрастании напряжения в толстых нитях [142]. Развивая эти идеи, Чаплен и его сотрудники предложили ки­бернетическое описание ЛМН, основанное на теории регули­рования [146—148]. Подробный анализ автоколебаний ЛМН, исходящий из модели А. Хаксли, проведен Абботом [214].

Мы не располагаем пока количественной теорией автоколе­баний ЛМН, тем более, молекулярной теорией. Необходимо обоснованное получение кинетических уравнений и нахождение их нестационарных решений. По-видимому, в этих уравнениях будут фигурировать в явном виде упругие элементы, имеющие молекулярное истолкование. Ясно, что автоколебания ЛМН представляют собой четкую и весьма интересную физическую проблему.