ФИЗИКА ЖИЗНЕННЫХ ПРОЦЕССОВ

ИНИЦИАЦИЯ МЫШЕЧНОГО СОКРАЩЕНИЯ

Предшествующее изложение ограничивалось стационарным сокращением мышцы. Не меньший, если не больший интерес представляют нестационарные кинетические процессы в мышеч­ном волокне.

Первая стадия сокращения — его инициация ионами Са4"1-, вы­ходящими из саркоплазматического ретикулума под влиянием электрического импульса. Импульс передается либо по аксонам нервных клеток, либо путем прямого электрического стимули­рования мембраны мышечного волокна. При стимуляции мы­шечного волокна коротким электрическим импульсом возникает напряжение, развитие которого во времени выражается кривой с максимумом и перегибом [130]. При стимуляции серией корот­ких импульсов напряжение выражается совокупностью пико- образных кривых, причем каждый последующий максимум лежит выше предыдущего, пока не достигается стационарный режим. При больших частотах пики сливаются, образуя экспо­ненциальную кривую гладкого тетануса [131]. В этих условиях потенциал на мембране волокна меняется в течение опыта. В ра­боте [132] были проведены измерения изометрического напряже­ния при фиксированном потенциале. Развитие напряжения во времени описывалось суммой двух экспонент. Из температурной зависимости скорости процесса получаются барьеры <?! « 19—20 иб!« 15—16 ккал/моль. Вместе с тем высота барьера для диф­фузии Са++ из ретикулума, определяемая по скорости насыщения ретикулума нонами Са++ [133], составляет 18—20 ккал/моль.

В работе [39] рассмотрена соответствующая двухбарьерная модель — первый барьер Gj соответствует диффузии Са++, второй G2 — замыканию мостнка, расщеплению АТФ и конформацион - ному переходу. Этот барьер соответствует рассмотренному в предыдущем разделе. Профиль свободной энергии изображен на рис. 5.24. Минимум / на рис. 5.24 соответствует состоянию си­стемы, в котором большая часть Са++ сосредоточена в мембране ретикулума, 11 — состоянию, в котором Са++ находится в сарко­плазме или на мостике до его замыкания, III — на сработавшем мостике.

На основании опытов по локальной деполяризации мышеч­ного волокна предполагается, что напряжение ф, приложенное к его мембране, передается на мембраны саркоплазматического ретикулума. Ранее уже были проана­лизированы различные модели уча­стия ионов Са++ в механизме измене­ния ионной проницаемости мембран нервных волокон под действием элек­трического поля (см. § 4.4).

100)

(5.101)

Пусть х\, х2, х3— числа ионов Са"^ в состояниях /, II, III-, Ы — их сум­марное количество. Предполагается, что х3 <С xi - f - х2 и, следовательно, N Xi х2. Кинетические уравнения имеют вид

К\ = k~xN — (k\ + k-\)x\, х3 = k2N — k2x\ — k-2x3

Константы скорости указаны на рис. 5.24. Решение уравнений (5.100) записывается следующим образом:

(0 = . + (х\ (0) — xi J ехр vif

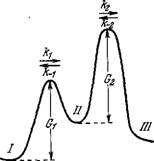
Рис. 5.24. Профиль свобод­ной энергии.

*з (0 = *з+ « ехр Yi* + Р ехр \2(

Где Yi=—{k\ Y2=fe-2, и x3oo — стационарные значення

X\ и x3. Константы аир находятся из начальных условий. Имеем

N

1 + Ki

(5.103)

Х\^ = К\К2х3с — Л' Kl

(5.102)

Где К\,2 — к-и-2Ік\,2- в принятой модели Кі = ехр (- ф ZT/RT)-,

Здесь г— валетность частицы, Т —число Фарадея. Таким обра­зом, k\, зависят от ф.

Можно считать, что при изометрическом сокращении напря­жение, стимулированное импульсом, пропорционально числу
замкнутых мостиков, линейно зависящему от х3. Таким образом,

P(t) = g[x3(t)-x3], (5.104)

Где g — константа, х3— значение х3 при потенциале покоя. Из (5.102) и (5.104) легко найти стационарное напряжение Рж. Вводя безразмерные переменные я в= P^KJgN, (p = q>&~/RT, получаем

П 1+ехр(— 2ф) 1 + ехр (— 2ф0) ' (5.105)

Где фо — потенциал покоя в единицах RTjtF. Находим

"5ф = 2 [1 + ехр (-1ц>)}2" (5.106)

В точке перегиба кривой я(ф) имеем ехр(—2ф) = 1, т. е.

Dn d(р

(5.107)

Z

Перегиб 4

Опыт дает значение этой величины, близкое к 1 [132]. Следова­тельно, 2 ~ 4, что может означать перемещение двухвалентных ионов Са++ парами. При длительной фиксации потенциала пара­метры системы меняются один раз — в начале деполяризации. Начальные условия имеют вид

(0) = хи х3(0) = х3. (5.108) Константы а и р во втором уравнении (5.101) равны

А^-^Г^с-^з); Р = ^г(*з«-*з). (5.109) Из (5.102), (5.104) и (5.109) следует

Р (0 = р - (1+ ехр V,/ - ^^ ехр vrf) • (5.110)

Такой характер зависимости P(t) при фиксированном потен­циале согласуется с опытом.

При кратковременной деполяризации внешние параметры ме­няются дважды: в момент наложения потенциала t — 0 и в мо­мент его СНЯТИЯ t = Т. Допустим ДЛЯ простоты, ЧТО I Yl,21 х 1. На отрезке времени 0—% переменные ведут себя согласно си­стеме уравнений (5.100) при начальных условиях (5.108). Огра­ничиваясь линейными членами по Yi,2t, находим

Хх (г) « X! + (*i — х! ф) Yit, І

Хз(т)~х3, > (5.111)

*зСО«(*зФ — х3) YlY2^, >

Где лгіф и лгзф — равновесные значения Х\ и х3 при потенциале <р. Из (5.104) следует

Р(т)да0, Р(х)^у1у2хР00. (5.112)

Это — начальные условия для развития напряжения при t > т. Равновесное напряжение в этих условиях равно нулю. Имеем при t> х

Р V) = 7 [- «Р VI (/ - т) + ехр y2(t - т)]; (5.113)

Yi есть значение уі = —+ при потенциале покоя ф = фо. Кривая, описываемая (5.113), имеет максимум при

И точку перегиба при t = 2tm. Это подтверждается опытом [130]. Максимальное напряжение при одиночном изометрическом со­кращении равно

= • (5.114)

В работе [33] получено также более общее выражение для Ртах(т), выведенное без ограничения |ym|t < ^ ®Н0 имеет вид

/ Vo \ - Vi/(Vi-Vi)

Ршах = (1-ехру1т)Рсо(^-) X

Xfl +—Л +_v=_

^L ' Ya (1 — ехр \,т) Ч ' —\2 F T1

-^7ЄХРЇ2т)] . (5.115)

Экспериментальное значение РШах(т) линейно растет с т при малых т и достигает насыщения при т да 270 мс [132]. Формула (5.115) прекрасно согласуется с опытом.

Та же модель объясняет развитие тетануса при стимулиро­вании мышцы серией коротких импульсов. Для напряжения, вызванного i'-м импульсом, можно написать аналогично (5.113)

+ Рі(х)~Хі{х) <5-ii6>

Начало отсчета времени в каждом периоде свое. Положение на общей шкале времени определяется номером периода і. Началь­ное напряжение Рі(х) и скорость его изменения Pj(-c) меняются от периода к периоду. Связь между ними можно установить с помощью системы уравнений (5.100)

Р, (Т) = й-2 [§ {М~2'(Х) - - P^(т)] • (5-117)

Величина *і, ї (т) находится путем последовательного решения первого уравнения системы (5.100) с двумя скачками парамет­ров в каждом периоде. Для і-го импульса в области т ^ t ^ Т (Т — длительность периода) получаем

І (0 = + [(*іф — х{) — (х1ф — xi, і (0)) ехр yit] ехр yi (t — t). (5.118}

Начальные условия, имеющие смысл условий непрерывности, запишутся как

*ы(0) = *ы-1(7"); і(0) = *і - (5.119)

Решение цепочки уравнений (5.118) и (5.119) дает

І (т) = *1ф +

+ (і, - *1ф) ехр Y, T[l + (1 - ехр(- y, t)) 1 ^-І^Ґ]' (5-12°) где

K = bT + (Vi~Vi)r - (5-121)

В частном случае, когда частоты v=l/(T — т) малы, из (5.120) получается *і, ї(т) = *і, і(т), т. е. в течение периода Т система успевает прийти к исходному состоянию. Когда после начала наблюдения прошло достаточное время, т. е. ехр[(( — 1)х] «С 1, из (5.120) следует

' <т> = - *'*> ехр v (Т~-7)-Zl YIT) • (5.122)

В предельном случае очень больших частот Т->т имеем Хі, і(т)—» ~*xlv. Подставив (5.122) в (5.117) при условии Iyi^ItCI по­лучаем

= 4 ехр(5.123) Максимальная величина функции Pt(t) равна

Рі max ) =

= \Рі(т) — — Pl(r) 1Г* ^W-^Wl-"^. (5.124)

L 'K ' Y2 JLY. Pi (Г) - ViPt (T) J V '

Условие стационарности режима состоит в равенстве напряже­ний в начале и в конце каждого периода. Пользуясь этим усло­вием, получаем из (5.116)

(Y2 - Yl) Pi (т) = (Т) - Pi (*)] ехр Yl (Т-г)-

- [ЬРі « - Pi (T)J ехр Y2 (Т - т). (5.125)

Решая уравнения (5.123) и (5.125) относительно Р{(т) и РДт) и подставляя решения в формулу (5.124), получаем зависимость Pi max от частоты в стационарном режиме:

Ft mtxW exp(Y,/v)-1+y. Ly2 1-exp(Y,/v) J '

В двух предельных случаях очень больших и очень малых частот (напомним, что yi, Yi> У2 < 0)

Lim Pt max = P„, lim Pt max - - yitPco (Y./Y2)W(V!"W.

V-»oo v-»0

Первый случай соответствует фиксированному потенциалу, вто­рой совпадает с формулой (5.114) для одиночного импульса.

Экспериментальный график зависимости Pim ax(v) выра­жается кривой с перегибом [131]. Дифференцируя уравнение (5.126), можно показать, что dP{ maJdv > 0 и стремится к нулю при v —»0 и v —► оо. Теоретическая кривая также имеет перегиб.

Р, „ 1 / v„4-Vi/(Vi-'?i) rі max 1 \2 \

Pi max Yi^

Сравним максимальную величину напряжения при одиноч­ном сокращении (5.114) с Pjmax при больших частотах в ста­ционарном режиме

/ V„ \ YIU T2 ТІ/ №) • <5Л27>

Опыт дает для этого отношения величину, равную нескольким единицам [131]. Если бы на том же объекте были проведены опыты, из которых находят параметры уь Yi> Y^- можно было бы с помощью выражения (5.127) дать теоретическую оценку этой величины. Yi и Y2 можно найти из кривой для единичного ответа. Для оценки Yi нужно иметь серию кривых одиночного ответа для разных т.

По параметрам напряжения при одиночном сокращении мож­но теоретически предсказать также форму кривой для случая тетануса. При больших частотах можно в выражении (5.116) разложить экспоненты в ряд и заменить кривые в каждом пе­риоде отрезками прямых, а затем получившуюся ломаную ли­нию заменить гладкой кривой. Ее уравнение имеет вид

P(0-P«(l-expYrf). (5Л28)

Параметр у2, найденный из одиночного ответа, равен 27 с-1 [131]. Согласно (5.128), он определяет и форму кривой для гладкого тетануса. И действительно, опытное значение уг. полученное из экспериментального графика для гладкого тетануса [131], равно 25—28 с-1.

Таким образом, теория, предложенная в работе [39], объяс­няет количественно большую совокупность опытных фактов. Мо­дель, лежащая в основе этой работы, согласованна с моделью, принятой при рассмотрении стационарного сокращения мышцы и описанной в § 5.7.