ФИЗИКА ЖИЗНЕННЫХ ПРОЦЕССОВ

ГЕНЕРАЦИЯ ИМПУЛЬСА

Проблема генерации нервного импульса в ответ на раздра­жение аксона исследовалась экспериментально и теоретически во множестве работ. Ей посвящены фундаментальные моногра­фии, среди которых назовем труды Ходжкина [3], Тасаки [6] и Ходорова [8,94]. Эта проблема уже затрагивалась в §§ 4.1 и 4.2. Трудности ее изучения в значительной мере связаны с отсут­ствием прямой информации о соответствующих молекулярных процессах. Приходится строить теоретические и полуэмпириче­ские модели, основанные на косвенных данных, полученных в опытах, в которых мембраны подвергаются различным физиче­ским и химическим воздействиям.

Из формальных математических исследований, описанных выше, можно заключить, что распространение и генерация им­пульса определяются формой трансмембранного тока — специ­фикой его зависимости от потенциала и времени. В свою
очередь особенность вольт-амперной характеристики мембра­ны— наличие участка с отрицательным наклоном — является следствием зависимости Na - и К-проводимостей от потенциала на мембране. Следовательно, поиски физической сущности воз­буждения сводятся к исследованию механизмов, определяющих зависимость проводимостей и по­тенциала от времени.

Проведем прежде всего полу­эмпирическое рассмотрение ос­новных характеристик генера­ции [63].

Рассмотрим возникновение потенциала действия в однород­ном участке нервного волокна. Так как на первом этапе деполя-

(4.28)

'Na

: &Na (ф - Ф. Ча)-

Как мы видели, зависимость ЈNa(<p) S-образна. Причины этого

/

Na

Рис. 4.18. Зависимость /Na от времени.

Ризации К-проводимость очень мала, считаем ионный ток сум­мой тока утечки /у и Na-токэ /nа - Ток утечки выражается по закону Ома как отношение изменения потенциала <р і|з — і|з0 (■фо—потенциал покоя) к сопротивлению мембраны R:

/У = <р/Я.

Зависимость /n а от времени аппроксимируем прямоугольной «ямой», показанной на рис. 4.18, где t* — момент достижения током его пикового значения, —момент спада Na-токэ.

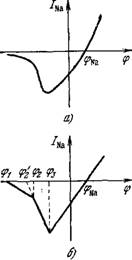
Рис. 4.19. Экспериментальная вольт-амперная характеристи­ка (а) и ее аппроксимация ло­маной линией (б).

Опыты при фиксированном потенциале показывают, что за­висимость /Na(<p) нелинейна. Это обусловлено зависимостью gNa(<p). При мгновенном СКаЧКЄ потенциала проводимость gNa не успевает измениться и, как показывают опыты Ходжкина и Хаксли [3], /Na линейно зависит от разности потенциалов
рассмотрены ранее в § 3.6. В результате наблюдается вольт - амперная характеристика с падающим участком (рис. 4.19,а). Заменим эту кривую ломаной линией (рис. 4.19,6) и введем gи g2 — абсолютные величины Na-проводимости

Dl

Na

8i = g2 =

Гіф d/,

(4.29)

Na

Гіф

При ф[ < ф < ф2> при ф > ф2.

Вольт-амперная характеристика для пикового Na-токэ опи­сывается формулами

0.

Ф < Фі, Фі < Ф < Ф2, Ф2 < Ф < Фз, Ф> Ф3.

Мф — ФІ).

G2 (ф — Фа), £2(ф~

1 Na

(4.30)

Причем gi < g < g2, где g = R~l. При возбуждении мембраны постоянным током от источника с напряжением ф имеем I = = g<p. Рассмотрим ответы мембраны на такое раздражение.

Если ф<фь то /на = 0, U = /у. Уравнение для мембран­ного тока I т == С -"^гт—І і принимает вид

Гіф 1Г

Его решение

■■ g (ф + Фо — ф).

Ф — Фо = ф[ 1 — ехр (— /)].

Это уравнение описывает пассивное поведение мембраны при подпороговых стимулах. Величина стимула ф = RI определяет предел, до которого растет ф. Если в момент і = t0 стимулиру­ющий ток выключается, то

G (Фо — ф)

С начальным условием

(4,33)

Ф('О) = ФО + ф[і — ехр (-

Решение дает быстро спадающее напряжение

Йф

~df ~

Ф-ф0=^ф[ехр(-^/0) - О'

(4.34) Фо - Ре-

Шение (4.34) имеет вид

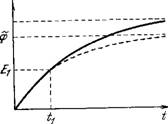
Рис. 4.20. Изменение мембран­ного потенциала со временем при раздражении постоянным током.

Пунктирная кривая —пассивный от­вет

G — Si

Gexp

Если стимулирующий ток достаточно велик, то наступает момент I = t\, в который растущий потенциал <р достигает ве­личины фі. Рассмотрим ответ на действие длительного стиму­ла. Имеем

С 4f" = — Є (Ф — Фо) + gi (Ф — Фі), / > /1.

Введем следующие обозначения: Е = ф — ф0, Е\ = фГ Е

(/-/,)]]. (4.35)

Так как g > gi, то величина E(t) растет, если ф> Еи до значения

= 1іт£ = ф +

+

T-* оо

Ві

(ф-£і)>ф. (4.36)

G~g 1

Картина роста потенциала имеет вид, показанный на рис. 4.20. Локальный ответ определяется как разность наблюдаемого сдвига потенциала и соответствующего пассивного ответа. Вы­читая (4.32) из (4.35), находим

Gl — gexp

G — g і

Ф — Г - ві L

(4.37)

Мы видим, что (ср. (4.32))

(ф — Ei).

(4.38)

G — g і

Lim Елок = 0, lim Ел0к =

Вычисление производной дает

<^ок _ {ф _ Ei) ехр JL^L (/ _ ^ _ в. ф ехр X,) ,

Dt

D2Em dt2

DEx

= 0; lim

>0.

Lim t-+t,

Dt

(4.39)

Из уравнений (4.37) — (4.39) следует, что локальный ответ имеет S-образную форму (рис. 4.21), как и наблюдается экспери­ментально [64].

Согласно уравнению (4.32)

Фі — ф0 = £і = ф(і —ехр (— -^/і))-

Исключив с помощью этого соотношения ехр ^—из УРа" внения (4.35), находим

Я = Ф + ££ [ft - Ї ехр (- ,) (^Г"'*] ■ (4.40)

Зависимость Е от стимула ф нелинейна.

Расчет дает кривую £(ф), показанную на рис. 4.22. Экспе­риментальная кривая имеет ту же форму [65].

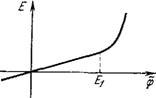
Рис. 4.22. Зависимость сдвига мембранного потенциала от приложенного стимула.

Ет

Рис. 4.21. Зависимость локального ответа от времени.

Мы видим, что рассматриваемая полуэмпирическая модель выявляет основные черты локального ответа: его S-образную зависимость от времени, градуальность, т. е. зависимость от величины стимула, и нелинейный характер этой зависимости. Все эти черты обусловлены появлением тока через мембрану, определяемого отрицательной дифференциальной проводимо­стью, абсолютная величина которой gi меньше мембранной про­водимости g.

В отличие от того, что наблюдается в эксперименте, наша модель приводит к появлению «порога» для локального ответа. Причиной этого является упрощение, согласно которому в точке «порога» происходит излом проводимости. На самом делг вы­ключение Na-тока происходит плавно, что должно повлечь за собой превращение точки перехода в некоторую область пе­рехода.

Допустим теперь, ЧТО предел Есо, к которому стремится сдвиг потенциала, превышает величину фг - Система оказывается в области, где Na-ток определяется отрицательной дифференци­альной проводимостью, абсолютная величина которой g2 > g. Так как g > gu можно считать gz gі - Пиковый Na-ток на
этом участке записывается в виде /Na = —£г(ф— фг)- Измене­ние мембранного потенциала описывается уравнением

С ^ = £ф — g (Ф — Фо) + g2 (ф — Фг)- (4-41)

Рассмотрим действие длительного стимула. В этом случае мо­мент t2, с которого начинается «действие» уравнения (4.41), приходится на участок подъема потенциала, описываемый уравнением (4.35). Решение уравнения (4.41) имеет вид

+ [ф Цг) + у (Ф + Фо) - yf=y Фа] ехр (/ - t2)]. (4.42)

Показатель экспоненты здесь положителен. Функция ф ра­стет неограниченно или падает в зависимости от знака пред - экспоненциального множителя. Если к моменту t2 потенциал равен фг, то предэкспоненциальный множитель положителен при условии ф І> ф2 — фо - Таким образом, начинается рост по­тенциала, не ограниченный величиной стимула. Потенциал ра­стет вплоть до момента времени t = t3, когда вследствие инак­тивации мембраны Na-ток падает. Если к этому времени пре­кратилось действие стимула, то поведение системы описывается уравнением

С = ~~ 8 (Ф ~ Ф°)'

Решение которого имеет вид

£ = £(/з)ехр[-£(*-*з)].-'

Потенциал падает экспоненциально до уровня потенциала по­коя. Весь ход ф(^) представляется кривой, изображенной на рис. 4.23.

Перейдем к рассмотрению поведения мембранного потен­циала при малой длительности стимула to. Для простоты пре­небрежем вкладом локального ответа в пороговый сдвиг мем­бранного потенциала, так как этот ответ просто суммируется с изотоническим ответом на раздражение постоянным током. Пусть действие стимула прекращается еще на изотоническом этапе развития мембранного потенциала. К моменту t = t2 по­тенциал достигает величины фг, но Na-ток не включается, пока не пройдет отрезок времени, равный некоторому лаг-периоду Дt. Но за это время действие стимула прекращается и начи­нается падение потенциала. Если к моменту времени t =

ОН не станет меньше ф2, т. е.

Ф (t2 + At) = Фо + Ф [ехр (-J /о) - 1] ехр [--§- (t2 + (4.43)

То включается Na-ток, дающий импульс (спайк), и наблюдает­ся картина развития потенциала, показанная на рис. 4.24.

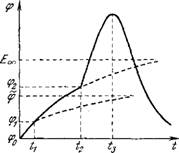
Рис. 4.23. Развитие мембранного по­тенциала во времени при длительном возбуждении током надпороговой ве­личины.

<Р

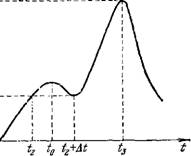
Рис. 4.24. Развитие мембранного по­тенциала во времени прн раздражении импульсом постоянного тока длитель­ностью ta.

11—момент начала локального ответа, t2—момент включения Na-тока, соответ­ствующего большой отрицательной диффе­ренциальной проводимости, 1.1—момент от­ключения Na-тока,

Из уравнения (4.43) можно получить соотношение между по­роговой силой тока / и длительностью его действия

E2g ехр (t2 + лої ' - L - J (4.44)

Ехр to) - 1

Так как t2 — время достижения ф2 при пассивном росте по­тенциала, то из уравнения (4.32) следует

Ф - Е2 __ I — gE2 _ ( g, \

И подстановка этого соотношения в (4.44) дает зависимость между силой тока и длительностью импульса

I = E2g\l+ \ ■ (4.45)

При очень малых t0 получаем приближенно

(4.46)

Е2С ехр А/)

I

Где Q — количество электричества, проходящее через мембрану при очень коротких пороговых толчках тока. При очень большой длительности импульса пороговая сила тока равна /п = E2g. Эта величина является реобазой (см. стр. 166). Характеристиче­ское время т8 определяется соотношением

Т, = <?//„.

(4.47)

(4.48)

С учетом уравнения (4.46) получаем Значение величины ///„ в точке t0 — xs равно

= 1 +

(4.49)

Ехр [(g/C) Щ ехр [(g/C) А/1 - 1

Для аксона кальмара RC = 0,7 мс. Время At « 0,3—0,4 мс. Подстановка этих величин в (4.49) дает 1,36—1,42; экспери­ментально найденное значе - ниє равно 1,38 [66].

Соотношение «сила — длительность» в единицах реобазы имеет вид

_/_ = і | ЕхР ЇМО д/1

/ті

Exp[(g/C)M-l ' (4.50)

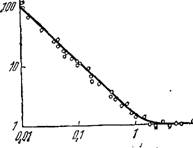
Форма кривой определяется теми же двумя независимы­ми параметрами g/C и At. Теоретическая кривая (4.50) представлена на рис. 4.25. На ней нанесены экспери­ментальные точки из рабо­ты [66].

10 Щ

Рис. 4.25. Теоретическая кривая зависи­мости «сила — длительность» в двойном логарифмическом масштабе и экспери­ментальные точки.

На основе принятой модели показано, что развитие спайка на мембране аксона начинается с того момента, когда мем­бранный потенциал достигает величины, при которой диффе­ренциальная проводимость отрицательна и превышает по абсо­лютной величине проводимость мембраны. Теория дает пра­вильное соотношение между силой тока и длительностью им­пульса.