ФИЗИКА ЖИЗНЕННЫХ ПРОЦЕССОВ

АКТИВАЦИЯ И ИНАКТИВАЦИЯ НАТРИЕВОЙ ПРОВОДИМОСТИ

Обратимся теперь к модельной теории активации и инакти­вации Na-проводимости. Такая теория предложена в работах [67—70].

В опытах на аксоне кальмара, проведенных методом фикса­ции напряжения на мембране, Ходжкин и Хаксли установили экспоненциальную зависимость между величиной начального изменения мембранного потенциала ф и пиковым значением натриевой проводимости gNa [5І]. Изменению ф на 4—6 мВ в сторону деполяризации отвечает е-кратное повышение gNa - Мо­жно предположить, что изменения ионной проводимости яв­ляются результатом влияния электрического поля на положе­ние каких-то ионов в мембране. Считая, что проводимостьgNa пропорциональна доле этих ионов, смещенных мембранным по­тенциалом из исходного положения, получаем

А = gna' m. ax (4 51)

Na 1 + 6 ехр (- zciq&IRT) v4

Где 2 — валентность гипотетического иона, а — число, выража' ющее долю напряжения ф, действующего на ион при его пере­мещении, b — множитель, не зависящий от ф. В области ф<0 получаем асимптотически

In gNa fa const - f zay@~jRT. (4.52)

Из Начального угла наклона экспериментальной прямой lngNa^) получается za ж 6 [51]. Параметр га можно опреде­лить также из центральной части кривой (4.51) по ее наклону в точке gNa = 0,5gNa, max [67]. Формула (4.51) хорошо согла - суется с многочисленными экспериментальными данными, по­лученными на различных аксонах [71—73]. Параметр za, най­денный по (4.52), имеет, согласно этим работам, значения от 3,6 до 6, по (4.51) —от 2 до 4,4. Среднее значение za равно 3,5.

Как уже сказано (см. стр. 178), Ходжкин и Хаксли предпо­лагали, что эти гипотетические ионы определяют активацию и инактивацию каналов для натрия и калия. Была высказана ги* потеза о том, что эти ионы — ионы Са**. Действительно, из­вестно, что изменения концентрации Са++ сильно влияют на возбудимость нервных и мышечных клеток [74] (см. гл. 5). Было показано, что при пятикратном изменении концентрации ионов Са++ кривые зависимости gNa, gK и инактивации от <р смещаются вдоль оси напряжения на 10—15 мВ. Понижение Сса смещает кривые в сторону меньших ф. Концентрация Са++ в растворе сильно влияет на скорость уменьшения gNa при сня­тии деполяризации. В цитируемой выше работе было выдви­нуто предположение о блокировании каналов в мембране ио-

7 М. В. Волькенштейн нами Са++. Отношение доли р каналов, закрытых кальцием, к доле открытых каналов 1 —р

РІІ1 - р) ОО сса ехр (- 2щТ! НТ), (4.53)

Где ссф— напряжение, под влиянием которого ионы Са++ пере­мещаются от внешнего раствора к месту закрытия канала. Если это место расположено в середине мембраны, то а = 0,5, если у внутреннего края, то а = 1,0. Согласно (4.53) е-кратное изменение Сса эквивалентно изменению ф не менее, чем на 12,5 мВ (если ее = 1,0). Между тем опыт дает от 4,5 до 9 мВ [71—73,75].

Вторая трудность «кальциевой гипотезы» связана со значе­нием га в формуле (4.51). а всегда меньше 1, 2 для Са++ рав­но 2. Между тем из экспериментального значения га « 3,5 следует, что 2 > 4. Предположение о том, что в блокировке каналов участвуют пары ионов Са++ наталкивается на суще­ственное противоречие — получается смещение кривой ^fNa (ф) , значительно превышающее наблюдаемое на опыте [67].

В работах [6, 19] исследовалось возбуждение мембраны аксона с помощью метода перфузии. Было установлено, что разбавление внешнего раствора изотоническим неэлектролитом повышает потенциал покоя. Аналогичное разбавление внутрен­него раствора не оказывает влияния. Напротив, замена С1_ во внешнем растворе на Вг~, SOI'h т. д. не влияет на потенциал покоя, а во внутреннем растворе она влияет на него. Следова­тельно, на внешней стороне мембраны имеется много фикси­рованных отрицательных зарядов, а на внутренней их мало. Возрастание внешней концентрации двухвалентных катионов стабилизует состояние покоя, а ее уменьшение приводит к за­метным флуктуациям мембранного потенциала. Ионы Са++ ока­зываются необходимыми для сохранения мембраны в состоя­нии покоя. На этих основаниях предполагается, что мембрана обладает свойствами катионообменника — в состоянии покоя доступные для обмена отрицательно заряженные центры на внешней стороне мембраны заняты двухвалентными ионами Са++. При стимуляции возникает ионный обмен. Процесс воз­буждения можно считать подобным фазовому переходу макро­молекул мембраны из одной устойчивой конформации в дру­гую. Обмен ионов Са++ на Na+ развивается кооперативно. Воз­буждение триггерно стимулируется переносом внутрь ионов Na+, замещающих внешние ионы Са++, причем изменяется физико - химическая структура мембраны.

Проведем, пользуясь методом молекулярного поля, анализ статистической модели возбудимой мембраны [67]. Предста­вим мембрану как совокупность периодически расположенных ячеек, каждая из которых может находиться в проводящем или
непроводящем состоянии. Проводимость мембраны пропорцио­нальна доле ячеек, находящихся в проводящем состоянии. Пред­положим, что энергия взаимодействия двух соседних ячеек рав­на ец, если их состояния одинаковы, и ею, если они различны. Разность е = ец — ею является параметром кооператнвностн. Каждая ячейка может присоединить ион валентности г, кото­рый при перемещении из раствора в мембрану пересекает поле с разностью потенциалов аф. Присоединение иона изменяет энергию ячейки на U + za<$9~ (в расчете на моль) и делает ячейку непроводящей. В приближении молекулярного поля по­лучаем

Ехр [ve (2р - 1 )/RT] ОО сса ехр (- zayP/RT), (4.54)

1 - р

Где v — координационное число. Это выражение совпадает с (4.53) в отсутствие кооперативности (при е = 0). Из (4.54) следует, что

(4.55)

(4.56)

Dp

P=0,5 2 (2 — p) ' ^ RT '

D(ygriRT) а так как gNa оо 1 — р, то

D (gNa/gNa, max)

D (фST/RT)

SNa^O'SSNa. max 2 ^ ^

В отсутствие кооперативности, т. е. при р = 0, эта производная равняется га/4. Как уже сказано, опыт дает za « 3,5. Такой же наклон кривой gNa(f) можно получить из формулы (4.56) при любых га < 4, если задать соответствующее значение р > 0. Таким образом, наклон кривой ^а(ф) можно объяснить при г = 2. Однако смещение кривой при изменении Сса с этим не согласуется. Из (4.54) следует условие смещения кривой

1п сса — zaq>!F/RT = const

И величина изменения ф при е-кратном изменении Сса равна Аф — 25/га (в мВ) независимо от значения р. Совпадение этого значения Дф с опытом получается лишь при za т 3,5.

Отсюда следует, что одновременное объяснение двух, не­сомненно связанных друг с другом эффектов, — формы кривой §Na (ф) и смещения этой КрИВОЙ При ИЗМЄНЄНИЙ Сса, НуЖНО искать на основе другой модели. Резкое возрастание проводи­мости обусловлено перемещением внутри мембраны заряда ве­личины 2 ^ 4, которое должно быть связано с десорбцией од­ного иона Са++. Если заряд совершает в поле работу гссфЗ2", где га — 3,5, то для получения согласия с опытом надо при­нять близкое к нулю значение р, т. е. малую кооперативность или ее отсутствие.

Модель, объясняющая основные экспериментальные факты, предложена в работе [68].

^Са + А^В.

(4.58)

Допустим, что в мембране имеется N ячеек, каждая из ко­торых содержит молекулу или группу молекул (активирующую частицу, способную находиться в состоянии[3]) А или В. Пред­положим, что переходы А В связаны с совершением работы в электрическом поле. Такие переходы могут состоять в пере­мещении заряженной молекулы, в поворотах диполей или в конформационном превращении макромолекулы, приводящем к одновременному перемещению нескольких зарядов. Последний вариант подтверждается опытами, свидетельствующими о нали­чии структурных изменений мембраны во время увеличения проницаемости [76, 77]. Если г — суммарный заряд, перемещае­мый при переходе А—* В, то работа моля частиц равна гаср^. Предположим, что в состоянии А частица образует комплексы А • Са с ионами Са++. В состоянии В активирующая частица обладает такой структурой или положением, что способствует прохождению иона Na+ через мембрану. Перенос Na+ лимити­руется числом частиц в состоянии В. Обозначим числа активи­рующих молекул в состояниях А и В через х к у, а число комп­лексов А • Са через s. Имеем

§т = кУ-

Таким образом, исследование временных изменений проводи­мости при сдвиге ф сводится к изучению зависимости y(t). Модели отвечает схема реакций

(4.57)

У = k2X — k-2y, s = k^c^x kis, x + y + s = N.

Из изложенного выше следует, что пиковой Na-проводимо- сти соответствует значение у, близкое к равновесному значе­нию yeq. В стационарных условиях, т. е. при у = s = 0, из (4.58) получаем

(4.69)

Где Ki = k-i/ky. Учитывая значение /С2, получаем £ка = = ^Na, шахД1 + С1 + *>ССа) Я *ХР (- ^f-)] , (4.60)

Где gNa. max = kN (k — коэффициент пропорциональности). Как МЫ видели, экспериментальная форма кривой gNa(tp) хорошо описывается формулой такого вида, если га « 3,5. Смещение кривой (4.60) вдоль оси ф при изменении сса дается условием

(1 + KlCca)q ехр = const. (4.61)

Если К\ ссі» что согласуется с представлением о комплек­сах А ■ Са как о резервуаре активных частиц [68], то из (4.61) следует

1п ССа — 20^Г = const (4.62)

И величина Аф при е-кратном изменении сса равна RT/za&~, что дает 7 мВ при га — 3,5. Это хорошо согласуется с опытом [71, 73, 75]. Такие же смещения кривой £ка(ф) вызывают другие двухвалентные ионы: Mg++, Со++, Cd++, Ва++, Zn++ и Ni++. Оче­видно, что они могут замещать Са++ в рассматриваемой модели.

Кривая ЈNa(<p) смещается также при изменении рН [63]. При рН < 5,5 Аф == 13,5 мВ, при рН > 5,5 Аф == 1,3 мВ при е-кратном изменении концентрации Н+. Если ионы Н+ могут попарно связываться активирующими частицами в состоянии А, то их требуется в два раза больше, чем ионов Са++. Условие смещения (4.62) приобретает вид

In (1 + /Сі [н+]2) - zaq>&-/RT = const (4.63)

И, если /Сі[Н+]2> 1, то

2 In [Н+] — zayST/RT = const. (4.64)

Увеличение [Н+] в е раз равносильно уменьшению ф на вели­чину

Аф = 2RTlza&~ = 2RT/3,b3T = 14 мВ,

Что совпадает с опытными данными в области рН <; 5,5.

При малых [Н+], если /Сі[Н+]2<1, формула (4.63) также приводит к совпадению с опытом [68].

В нестационарных условиях решение уравнений (4.58) имеет вид

У (0 = г/о + г/і ехр (г+ у2 ехр (га/). (4,65)

Кривая, описываемая (4.65), имеет S-образную форму (рис. 4.26), что согласуется с видом экспериментальной кривой gNa (0- Константы Уі и г і зависят от параметров системы ku k-i, N, сса - Подобрав численные значения констант, можно до­биться полного согласия теоретической кривой (4.60) с экспе­риментальной. Аналитическое исследование y(t) позволяет установить зависимость начальной скорости изменения gNa(O) от сса - Расчет дает эту начальную скорость [68]

GNa (0) = - k_x NcCaK2/( 1 + Ks). (4.66)

Опыт подтверждает линейную зависимость скорости падения gNa от Сса при снятии деполяризации. Действительно, пониже - у ниє Сса в пять раз от 112 до 22 мм умень-

Шает скорость изменения gNa также в пять f раз, а от 112 до 4,4 мм — в 25 раз. Из

/ формулы (4.66) следует также, что, ском-

/ пенсировав уменьшение Сса изменением ф

/ так, чтобы произведение /Сг^са оставалось

J постоянным, мы должны наблюдать умень-

^— шение скорости падения gNa, потому ЧТО Ki

T входит еще и в знаменатель. Рис. 4.26. График ^а же модель позволяет рассчитать

Функции y(t). влияние Сса НЭ кинетику подъема gNa при возникновении деполяризации [68]. В согла­сии С ОПЫТОМ теория дает замедление скорости роста gNa при увеличении сса-

Таким образом, модель объясняет большую совокупность фактов, относящихся к Na-проводимости клеточной мембраны. Можно думать, что сходный физико-химический механизм оп­ределяет и изменения К-проводимостн.

Рассмотрим теперь инактивацию Na-проводимости возбуди­мой мембраны.

Ходжкин и Хаксли высказали две альтернативных гипотезы о природе повышения gNa [50]. Первая из них предполагает химическое превращение активирующих частиц после их пере­мещения из положения, которое они занимали при потенциале покоя. Вторая предполагает, что уменьшение gNa обусловлено перемещением особых инактивирующих частиц, постепенно блокирующих каналы проводимости. Вторая гипотеза при­нята в теории Ходжкина — Хаксли (см. стр. 179). Модель, предложенная в работе [67], исходит из первой альтерна­тивы.

При потенциале покоя активирующие частицы находятся преимущественно в состоянии S, когда они связаны с Са++ и А. Эти состояния отвечают отсутствию Na-проводимости. При де-
поляризации мембраны происходит переход А->В в проводя­щее состояние, связанный с перемещением заряда z в полеаср. Из состояния В активирующая частица может переходить в не­активное состояние С. Этот переход не связан с перемещением заряда. После снятия деполяризации происходит переход С —► S ( = А • Са) с работой заряда zaq>@~. Схема этих процес­сов показана на рис. 4.27. Соответствующая система кинетиче­ских уравнений имеет вид

X=k]s — k-ixc са + k-2y — k2x, у = k-3u — k3y — k-2y + k2x, й — — k-3u - f k3y + &-4s — kiUCa, x-\-y-\-и-\-s=l.

Здесь x, y,u, s — доли молекул в состояниях А, В, С, S (== А ■ Са) соответственно, сса — концентрация Са++ в омываю­щем растворе. Как уже сказано, gNa = ky (см. стр. 196). Исследова­ние изменений gNa ВО времени СВО­ДИТСЯ к определению y(t).

Считая, что в реакции II быстро устанавливается равновесие (это со­гласуется с наблюдаемым ' влиянием сса на кинетику активации), заменим первое уравнение (4.67) на

Х = К2у, (4.68)

Где константа равновесия К\ = k-ijki. Константы К\ и Кз, очевидно, не свя­заны с перемещением зарядов в поле и не зависят от <p. К2 и К4 должны зависеть от <р согласно фор­мулам

= Я2 ехр (— zaq>&~/RT); КА = q4 ехр {zayST/RT). (4.69) Система уравнений (4.67) приводится К ниду

6-ТТЖ7І1 - 0 + + +it) У ~ О ~ ТГ) "]• 1

(4.67)

II

Ь

Рис. 4.27. Схема процесса активации и инактивации Na-проводимости [50].

I к,

К3 пі

К4 Ж

(4.70)

Нужно найти корни г\, г2 характеристического уравнения си­стемы

+ [тТ7с7([4] + + ССа*Л) + Л-4 ( 1 + +15:)] '+

+ ТТТ7 [О + *« + сс.*Л) (1 + W, + -

+ = (4.71)

Комплексным корням соответствует переход системы в стацио­нарное состояние в результате затухания колебаний около этого состояния. При фиксированном потенциале ионные токи не ис­пытывают затухающих колебаний. Ищем решение (4.70) с ве­щественными корнями г і и г2. Они отрицательны и решение за­писывается следующим образом:

У (0 = аі + 6, ехр (- | п Ю + сі ехр (- | г210, и (0 = а2 + Ь2 ехр (- j г, 10 + с2 ехр (-1 г211). (4J2)

Введя начальные значения у0, и0, уо, ы0 и равновесные значения

Уоо, и», отвечающие t-+oо, получим

Л — „ А — Уо + (Уоо — Уо) Г[ — г2

С _ Уо+ /-1 (у^ — Уо)

' /"2 — г,

И аналогичные выражения для а2, с2. Функция y(t) может иметь макси­мум в момент времени

T* ±= - 1 In Г2 + Г] (Уа> '

Г\ — Г2 г, [г/о 4- Г2 (уж — г/о)1 '

Необходимые и достаточные условия существования максимума суть

Уо + гх {уж — уо) > 0, Уо + г2 {ух — Уо) > 0. Точка перегиба соответствует

R = 1 1п Г1 [3?о + {Уо° - Уо)] ^

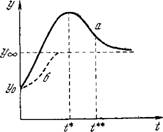
Рис. 4.28. Вычисленная за­висимость у (t), т. е. gNa (/).

А —кривая при наличии макси­мума, б— кривая без максимума.

R{-r2 r'i [г/0 + /-2 (»» - Уо)] '

T**>i*, т. е. точка перегиба лежит вправо от максимум? (рис. 4.28). Если условия появления максимума не выполнены, то кривая имеет лишь перегиб (кривая б на рис. 4.28). Сказан­ное относится и к u(t). В системе уравнений (4.70) при началь­ных условиях уо л? «о 0 Получается г/о ~ &i/(l + К2), «о ~ 6-4.

Из опыта известно, что инактивация развивается существенно медленней, чем активация. Поэтому следует предположить, что скорости реакций III и IV (см. рис. 4.27) малы по сравнению со скоростями реакций I и II, т. е.

Ku /г_ь k2, /г_2>/г3, /г_3, /г4, /г_4. (4.73)

Поэтому г/о «о и y(t) имеет вид кривой а (см. рис. 4.28). Если бы мы отказались от принятого адиабатического приближения, то кривая y(t) имела бы второй перегиб при і < t* (кривая б на рис. 4.28, ср. рис. 4.26).

Максимальное значение у равно

— „ У о + Аг ~ Г Уо + П (У — У о) г 2 у ■/(<•!-о) Утп-Усо ^ [уо + глу^-уо) ■

(4.75)

При выполнении условий (4.73) находим из (4.71)

_ К (1 + *2 + СсаЗД) Гі~ Т+Т2 '

_ *-4*С. Уі*2 + *з. у у

Г2~ 1 + /С2+ССаК,/С2 ССаК4-й-

Следовательно, J/-i|>j/-2|, rj(ri — r2)» 1 и формула (4.74) сильно упрощается:

У max — Уо• (4.76)

Подставляя в (4.76) значение г/0 из (4.70), получаем в конечном счете

Утих == (4-77)

И в пределе но—♦■О

= 1 + (1 + сСа*і) я2 «р.(- гщПЯТ) • (4-78)

Последняя формула совпадает с (4.60). Начальное значение и0 может отличаться от 0, оно зависит от исходного состояния мембраны. Стационарное значение «о, получаемое из (4.70) при у = й = 0, равно

1 +/С3 + (1 + сСа^) К2рК3

)ане, на которой дост потенциал фр. Введ

W — и I и* =1 — «л. v ах / "ma^ q

"о = ир = . „ . , • (4.79)

К2р соответствует мембране, на которой достаточно долго сохра­нялся предварительный потенциал фр. Введем отношение

Его значение для стационарного и0

1 + ехр (Za<!p! r/RT)/q2 (1 + сСа/С,) К3 ' (4'80)

Эмпирическая зависимость, найденная Ходжкином и Хаксли, имеет вид

W" — TZ 7~kr,—ГП^л' (4,81)

1 +ехр (фр/7)/ехр (фр/7)

Где фр — эмпирическое значение фр, отвечающее w = 0,5 (вели­чины фр и фр в мВ).

Как мы видели za ж 3,5, RT/&~ ж 25 мВ. Коэффициент при фр в теоретической формуле (4.80), определяющий форму кри­вой а>оо(фр), действительно равен za@~/RТ = 3,5/25 ж 1/7 мВ. Фактор ехр(—фр/7) в эмпирической формуле задает положение кривой а>оо(фр) относительно оси фр. Сравнивая (4.80) и (4.81), находим

Ехр(Ф;/7) = <72(1 + ссЛ)*з-

Положение кривой стационарной инактивации зависит от сса. Если Сса. Кі 1, то должно быть

CCa еХР — const.

Это значит, что е-кратное увеличение сса может быть скомпен­сировано уменьшением фр на величину Дфр = RTIzatF ~ 7 мВ. Опыт дает Дфр = 6,3 — 7,8 мВ [75].

Рассмотрим теперь развитие процесса инактивации во вре­мени. Если мембрана выдерживалась при потенциале фр недо­статочно долго, то «о в выражении w = 1 — и0 зависит от дли­тельности предварительного импульса, Uo = u(tp). При tp = 0 мембрана находится в состоянии покоя (соответствующие вели­чины снабжаются верхним индексом нуль). Из (4.72) и значений <h, Ь2, с2 следует с учетом малости начальной скорости изме­нения

Й Up) = Щ> + r/lri (Up — и0) [ехр (— | г21 tp) — ^ ехр (— | п | ґр)]

(4.82)

И, так как | r21 - С | г\ |, то

И (tp) + («° — ир) ехр (— | г21 tp),

Т. е.

W « 1 — Up — (и0 — Up) ехр (— I Г2 I tp).

Мы видим, что если мембрана до подачи тестового потенциала была гиперполяризована, т. е. ир < и0, то пиковый Na-ток ра­
стет экспоненциально с ростом tv\ если же ир > и° (деполяри­зация), то он экспоненциально убывает (рис. 4.29). Именно та­кой ход экспериментальных инактивационных кривых наблю­дался в работе [79]. В этой работе вводится величина тд, равная в излагаемой теории |г2|-1. Расчет дает

(4.83)

(4.84)

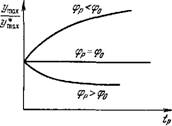
Рис. 4.29. Зависимость пико­вого Na-тока от длительности предварительного импульса — потенциала <рр. Фо — потенциал покоя.

. 1 КзО+^ + ССаЗД

Тй = I Г 21

Или, согласно (4.79),

K-3 + CCak4

Теория Ходжкина — Хаксли (см. стр. 177) дает

= wjx,

Где х— константа скорости выхода из инактивированного со­стояния. Знаменатель теоретиче­ской формулы (4.84) имеет тот же смысл. В теории Ходжкина — Хакс­ли зависимость параметров от tp подбирается искусственно с целью получения согласия с опытом; в из­лагаемой теории эта зависимость имеет непосредственное физическое содержание. Напишем (ср. (4.69))

Ki = л>4 ехр (— za(f>&~/2 RT),

/г _4 = v_4 ехр (zaqpS^/2 RT).

Как уже сказано, предполагается, что реакция смещена в сторону С, т. е. k-zlh < 1. При малых знаменатель в (4.84) приблизи­тельно равен (ф измеряется в милливольтах)

CCa^4==CCaV4eXP(-(P/14)-

Опыт дает и = 0,07 ехр(—qp/20).

Согласно теоретической формуле (4.83) тл(ф) представляется произведением двух противоположно направленных 5-образных кривых, т. е. тл(ф) имеет колоколообразную форму. При ф—»—оо тл—>0, при ф—»оо Такую же форму имеет экспери­

Ментальная кривая.

Согласно (4.83), максимум кривой та(ф) смещается в сторону больших ф с увеличением сса - Именно такое влияние Са++ на ве­личину xh наблюдалось в работе [75].

Таким образом, описанные кинетические модели действи­тельно дают количественное описание большой совокупности
явлений, наблюдаемых при генерации потенциала действия — при активации и инактивации мембраны. Вскрывается взаимо­связь различных явлений. Излоя-енная теория согласуется с экспериментальными фактами. Основная ее идея состоит в том, что переходы Ач=^В и S С связаны со структурными превра­щениями мембраны. Основной параметр теории — величина za. Опыт показывает, что при изменении проводимости мембраны аксона, при ее возбуждении, происходят структурные изменения. В работах [76, 80] наблюдались изменения рассеяния света. Тасаки и сотрудники наблюдали изменения флуоресценции [77], Берестовский и др. — изменение двулучепреломления мембраны аксона,.вызванное появлением потенциала действия [81].

Прямые доказательства перемещения заряженных частиц, входящих в структуру мембраны, под действием поля были по­лучены впервые Армстронгом и Безанилья, а затем изучены ими и другими исследователями более подробно [82, 83, 97].

При смещении мембранного потенциала в положительную сторону наблюдается изменение проводимости, при смещении в отрицательную сторону изменения нет. Следовательно, имеются «активационные ворота» — это свойство мембран нелинейно. Для нахождения реального тока заряженных частиц необходимо, во - первых, выделить нелинейные компоненты мембранного тока, и, во-вторых, связать их с процессом активации.

Чтобы обнаружить малый компонент трансмембранного тока, необходимо исключить мощные ионные токи, основную часть которых составляют токи Na+ и К+. В цитированных работах эти ионные токи подавлялись путем замены проникающих ионов иепроникающими. Ионы Na+ в наружном растворе заменялись ионами трис (оксиметил) метиламмония, а ионы К+ — ионами Cs+. Использовался также эффект Коля и Мура [97], позволяющий существенно замедлить развитие К-тока с помощью большой предварительной гиперполяризации мембраны.

Для устранения линейных токов утечки и емкостных токов применен метод алгебраического сложения сигналов, получен­ных от двух скачков потенциалов, равных по величине, но проти­воположных по знаку. Получающиеся суммарные токи очень малы. Поэтому для улучшения соотношения «сигнал — шум» применялась техника суммирования сигналов. Суммировались и усреднялись ответы от сотен и даже тысяч пар сигналов.

Каков источник зарегистрированных таким методом токов? Армстронг и Безанилья подробно доказывают, что это не токи ионов, приходящих из раствора. Следовательно, это токи сме­щения зарядов, являющихся структурной частью мембраны. Кейнес и Рохас [83] приводят следующие аргументы в пользу -того, что наблюдаемые токи являются токами смещения: 1) сум­марный заряд, смещенный при включении деполяризующего по­тенциала, с большой точностью равен суммарному заряду, сме­щенному при снятии деполяризации; 2) смещенный заряд, воз­растая с увеличением приложенного потенциала, достигает пре­дельной величины при достаточно больших импульсах; 3) пони­жение температуры не меняет полного заряда, перенесенного при прохождении импульса данной величины, хотя константа вре­мени имеет большой температурный коэффициент.

Идентификация несимметричных токов смещения с процес­сами, управляющими развитием Na-токэ, требует детального и разностороннего изучения свойств этих токов. В пользу связи между обоими процессами говорит близость их временных кон­стант (200—400 мкс). В аксонах, не дающих Na-токэ («dead axon pattern»), не наблюдаются и асимметричные токи смеще­ния. Внутренняя перфузия ЮМ рзствором ZnCl2 обратимо по­давляет Na-ток и несимметричный ток смещения. Ряд других свойств, по которым можно идентифицировать эти процессы, является в настоящее время предметом дискуссии. Требуются дальнейшие исследования, чтобы установить, каков механизм участия зарядов, дающих несимметричные токи смещения, в из­менениях Na-проводимости.

Процессы, определяющие изменения Na-проводимости, изу­чаются также на основе исследования влияния на нее различных ионов. Выше рассмотрено влияние Са++ и Н+ (см. стр. 196). Ионообменные процессы, как уже не раз указывалось, весьма существенны для поведения мембран. Эдельман и Палти изу­чали влияние ионов К+ в окружающем растворе на инактивацию №+-проводимости [84]. Параметр инактивации wx убывает с ро­стом концентраций К+, временная постоянная тл возрастает. Эти и другие явления также удается объяснить на основе кинетиче­ской модели, учитывающей ионный обмен [70]. Модель предпо­лагает, что центры, определяющие мембранную проводимость, могут существовать в двух состояниях. При переходе из одного состояния в другое производится работа заряда в электрическом поле. Одно из этих состояний (S) стабилизируется ионами Са++. При их замене ионами Na+ или К+ центр приобретает способ­ность к быстрому переходу в другое состояние, что приводит к высокой Na-проводимости, если ионы Na+ связаны с этим цент­ром. Связывание К+ переводит центр в состояние инактивиро- ванной Na-проводимости.

Сходная схема может объяснить действие других ионов на gNa, в частности, ингибирующее действие яда — тетро - дотоксина.

Кинетические модели не дают, конечно, полного молекуляр­ного истолкования обсуждаемых явлений. Здесь необходима дальнейшая экспериментальная работа, раскрытие тонких коли­чественных закономерностей. Но можно считать установленным.

Что в соответствии с развиваемыми представлениями о конфор- мационных свойствах мембран (см. § 3.8), их функциональные участки переходят из одних состояний в другие и эти переходы зависят от внешнего поля и ионного окружения.

Физика нервного импульса изложена также в обзоре [98].