EuroSun2008-2

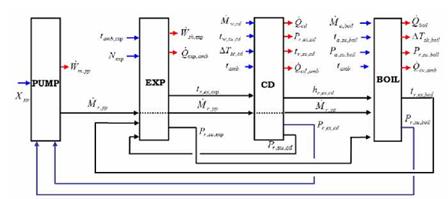
Validation of the global model of the cycle

Once the models of each component of the circuit are validated, these models are interconnected to simulate the whole system, as shown in Figure 8.

The following “causalities” are observed:

• the pump imposes the refrigerant flow rate,

• the expander imposes its supply pressure and exhaust temperature,

• the evaporator imposes the refrigerant superheating and the pump exhaust pressure,

• the condenser imposes the expander exhaust pressure and the pump supply pressure.

This simulation model is not fully predictive, because the subcooling at the exhaust of the condenser is defined as a model input. In order to predict this subcooling, a refrigerant charge model would have to be included.

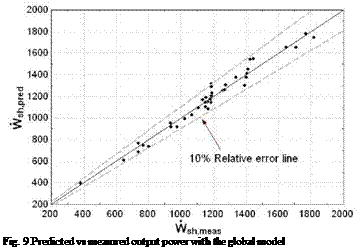Figure 9 shows the prediction of the output shaft power for the global cycle model. All measurements are predicted within a 10 % accuracy. Errors of each model are indeed cumulated, which leads to a lower accuracy for the global model than for the individual components.

4. Conclusion

This paper proposes a semi-empirical model of an ORC involving a relatively limited number of parameters. The comparison between predicted values and experimental results show a fairly good agreement (for the cycle model as well as for the different sub-models).

The experimental study carried out shows a good expander isentropic effectiveness and demonstrates the viability of utilizing a mass-produced compressor as an expander in a small scale ORC. This represents an important step towards realizing the cost reductions that would make a kilowatts-sized Solar ORC economical for developing countries.

That the overall cycle efficiency remains limited is partly explained by the low temperature of the heat source and by a low pump efficiency. The former can be rectified by using higher temperature heat sources, while the latter can be addressed by selecting of a pump optimized for the pressure ratio and flow rate of the ORC.

Future work will focus on the integration of the ORC model into a global model including the solar collector in order to size the system, define a control strategy, and optimize the working conditions and the components.

References

[1] Hung, T.-C., Waste heat recovery of organic Rankine cycle using dry fluids, Energy Conversion and Management (2001), Vol. 42, pp. 539-553..

[2] Incropera F. P., D. P. DeWitt, Fundamentals of Heat and Mass Transfer (2002), John Wiley & Sons

[3] International Energy Agency (2006), World Energy Outlook 2006, Paris

[4] E Kane, M., Larrain, D., Favrat, D., Allani, Y., 2003, Small hybrid solar power system, Energy (2003), Vol. 28, pp. 1427-1443

[5] Klein S., Beckman W. (2008), Engineering Equation Solver (EES), University of Wisconsin, Madison

[6] Liu, B.-T., Chien, K.-H., Wang, C.-C., Effect of working fluids on organic Rankine cycle for waste heat recovery, Energy (2004), Vol. 29, pp. 1207-1217.

[7] Lemort, V., Teodorese, I. V., Lebrun, J., Experimental study of the integration of a scroll expander into a heat recovery Rankine cylce, Proc. 18th Int. Compressor Engineering Conference at Purdue (2006), Purdue University, West Lafayette, C105.

[8] Maizza, V., Maizza, A., Unconventional working fluids in organic Rankine cycles for waste energy recovery systems, Applied Thermal Engineering (2001), Vol. 21, pp. 381-390.

[9] Price, et. al. Advances in Parabolic Trough Solar Power Technology, Journal of Solar Energy Engineering (2002), Volume 124, Issue 2, pg. 123

[10] Wei D., Lu X., Lu Z., Gu, J., Dynamic modeling and simulation of an Organic Rankine Cycle (ORC) system for waste heat recovery, Applied Thermal Engineering (2008), Volume 28, pp. 1216-1224

[11] Wenqiang, Liu, et. al. Techno-economic assessment for off-grid hybrid generation systems and the application prospects in China, World Energy Council (2007)

[12] Yamamoto, T., Furuhata, T., Arai, N., Mori, K., 2001, Design and testing of the Organic Rankine Cycle, Energy (2001), Vol. 26, pp. 239-251.