Case Study
The basic data of some solar power tower plant in China are as follows,
Plant Location: 115.97° east, 40.47° north.
Tower Height: 100m, Ht = 85m, Tower Width: 10m.
Distance between mirror centre of heliostat and ground: 10m.
Mirror Height: 10m, Mirror Width: 10m.
Ratio of net area of mirror to area of heliostat: 0.95, Mirror Reflectivity: 0.9.
Receiver Aperture Height: 4m, Receiver Aperture Width: 4m.
 |
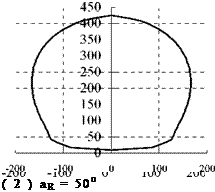 |
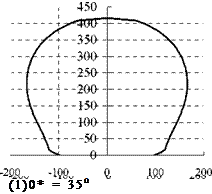
According to Fig.4 and formula (8), the receiver depression angle of this plant is 69.3o. Here, four heliostat field schemes whose receiver depression angles are 35o, 50o, 69.3o, 85o by respectively were compared and analyzed, field boundary lines are calculated by formula (1) to (7) and shown in Fig.5. Assumed that heliostats are arrayed as parallel and stagger pattern with same intervals, data are calculated and compared in Table 1.
( 1 ) aR = 69.3o ( 2 ) aR = 85o
Fig.5 Field boundaries with different aR
|
Heliostat Field Scheme |
Scheme 1 |
Scheme 2 |
Scheme 3 |
Scheme 4 |
|
Receiver Depression Angle (aR) |
35o |
50o |
69.3o |
85o |
|
Field Area (m2) |
91721.37 |
107190.09 |
115159.27 |
112153.66 |
|
Number of Heliostat |
83 |
96 |
98 |
92 |
|
Minimum Distance of Heliostat Field (m) |
0 |
0 |
0 |
8.5 |
|
Maximum Distance of Heliostat Field (m) |
323 |
374 |
416.5 |
425 |
|
Maximum Radius of Heliostat Field (m) |
165.75 |
165.75 |
165.75 |
165.75 |
|
Field Efficiency at 15 o’clock on Autumnal Equinox |
76.59% |
76.57% |
76.71% |
77.17% |
|
Cosine Efficiency at 15 o’clock on Autumnal Equinox |
88.67% |
88.66% |
88.92% |
89.14% |
|
Shadowing and Blocking Efficiency at 15 o’clock on Autumnal Equinox |
98.77% |
98.94% |
98.96% |
99.35% |
|
Radiation Reflected into Receiver at 15 o’clock on Autumnal Equinox (kW) (Assumed that Horizontal Direct Solar Radiation is 0.6kW/m2) |
5848.42 |
6761.89 |
6915.97 |
6531.09 |
|
Annual Average Field Efficiency |
77.97% |
78.01% |
78.16% |
78.55% |
|
Annual Average Cosine Efficiency |
90.89% |
90.90% |
91.17% |
91.41% |
|
Annual Average Shadowing and Blocking Efficiency |
98.08% |
98.31% |
98.34% |
98.62% |
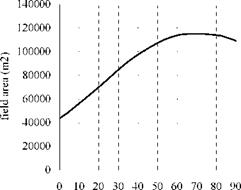
From Table 1 we can see that, the annual average field efficiency of the 4 schemes are subequal, with the maximum difference of 0.58%, and the field area of Scheme 3 is the largest one. The relationship between field area and receiver depression angle is shown in Fig.6(a). From Fig.6(a), we can known that the field area stays the maximum when receiver depression angle is about 70o.
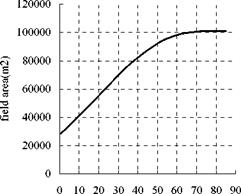
However, for the pratical layout of the field, as the tower can hid the heliostats nearby, which can lead the heliostat and field efficiency decrease if heliostats are too near to the tower. Therefore, some distance should be left when the first row heliostats are arrayed, which has been reported earlier [7]. Considering this, the relationship between field area and receiver depression angle is shown as Fig.6(b) with a distance of 0.75Ht.
From Fig.6(b) we can know that, the field area changes little when the receiver depression angle is great than 70o. Moreover, according to the discussion above, it is known that there is a little change in annual average field efficiency when receiver depression angle is changed. As a matter of
 |
 |
experience, furthermore, radiation spillage can be reduced because of receiver with a depression angle in conditions that heliostats have tracking error and rocking error. Therefore, Scheme 3 is the optimal one, and the rationality of the formula of calculating receiver depression angle is validated at the same time.
Receiver Depression Angle Receiver Depression Angle
(a) (b)
Fig.6 Relationship between receiver depression angle and field area
Based on the geometrical optics theory, the function of heliostat field boundary line was deduced, and the simplified formula to calculate the receiver depression angle with the only independent variable of latitude was given. Moreover, a certain Solar Power Tower in China was taken as the case, the calculated heliostat field data were compared for different receiver depression angle, and the rationality of the formula was demonstrated. From the results, the following conclusions were drawn. For the conditions of the same heliostat dimension and arrangement, it is optimal when the receiver depression angle is at around the value calculated by the formula of receiver depression angle developed in this paper. At the same time, the installed capacity of plant is mainly dependent on the height of tower and the area of receiver aperture. That is, the installed capacity of plant increases with the height of tower and the area of receiver aperture. On the other side, the installed capacity of the plant almost has nothing to do with the receiver depression angle in a certain range around its optimum value.
[1] Field Layout and CPC Researches in Tower Solar Power Plants and Roof CPV Design [D]. GUO Su: College of Water Conservancy and Hydropower Engineering, Hohai Univ., 2006: 65-80. (in Chinese)
[2] F. M.F. Siala, M. E. Elayeb. Mathematical formulation of a graphical method for a no-blocking heliostat field layout[J]. Renewable Energy. 2001(23):77-92.
[3] Marcelino Sa'nchez *, Manuel Romero. Methodology for generation of heliostat field layout in central receiver systems based on yearly normalized energy surfaces[J]. Solar Energy, 2006 (80) :861-874.
[4] Vant-Hull, L. L., 1991. Concentrator optics. In: Winter, C. J., Sizmann, R. L., Vant-Hull, L. L. (Eds.), Solar Power Plants. Springer-Verlag, Berlin, ISBN 3-540-18897-5.
[5] Stine W B, Harrigan R W. Power from the Sun[Z].www. powerfromthesun. net,2005.
[6] J. A. Duffle, W. A.Beckman. SOLAR ENERGY THERMAL PROCESSES. John Wiley & Sons, 1974:1
7.
[7] GUO Su, Liu Deyou. The Calculation of the Shadow and Block Efficiency of the Heliostats considering Tower Shadows in Tower SPPs[J]. Acta Energiae Solaris Sinica, 2007, 28(11):1182-1187. (in Chinese)