EuroSun2008-13

Equation developed in this study

Chen zhi-jun has quoted four statistical methods [5] to explain the data characteristic which are based on the monthly data of single station or based on the whole year data of single station or based on the monthly data of all stations or based on the whole year data of all stations. And the results show that the correlation of clearness index and sunshine percentage is to some extent spatial-dependence and time-dependence. And he also proves that the statistical method based on the monthly data of all stations is the best.

Followings are the figures of statistic result.

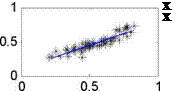
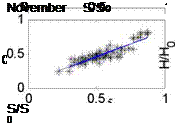
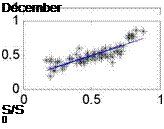
Fig. 1. The correlation of H / H о and S / S0 based on the monthly data of all stations in China

2.1. Comparative results

We can obtain the regression coefficient a and b (which are included in our model in the table 2) from the above Fig.1. To determine the predictive efficient of the model developed in this paper, it is pertinent to compare this model with those believed to be universally applicable (Eq10, 11, 12).And the result of these comparisons will determine the applicability of those models to China, as presented in Table 2.

2.2. Discussions

The errors of each model used in the estimation of global solar radiation are tested by calculating the mean bias errors (MBE), the root mean square errors (RMSE) and the mean absolute bias errors (MABE) from Equation (13), (14) and (15). The RMSE shows the discrete degree of the error, and the MABE shows the average status of the relative error, and MBE values obtained from the models are positive in some cases and negative in others, that means a positive MBE means over estimation and a negative MBE means under estimation. And it is observed that the lower the RMSE, the more the accuracy.

As can be seen in Table 2, our model has the best accuracy because the value of RMSE doesn’t exceed 6% which is the minimum in the four models, hence the estimation values of the global radiation can really reflect the real values. The performance of Page model (not exceed 7%)

is slighter better than that of Rietveld and Ogelman et al (they are 7% and 7.14%), the difference of accuracy is very little. With respect to MBE, the positive values of from the models (Rietveld, Ogelman et al, Page) indicate an over estimation, while the Ogelman et al’s model gives the worst over estimation, and our model only has very little under estimation. With respect to MABE, our model also has the minimum of these models and Ogelman et al’s model has the maximum.

By comparison, it is realized that the performance of the Ogelman et al’s model is the worst, and the performances of Rietveld’ (equationlO) and Page’ (equation 12) models are slight poor than that of the model developed in this paper.

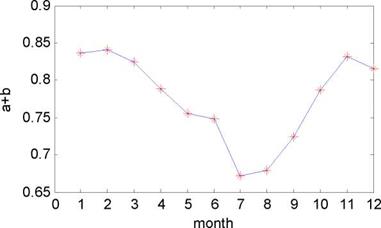
The transmissivity of the atmosphere for the global radiation under perfectly clear sky conditions is given as the sum of the regression coefficients, a+b[10] in the figure.2. We can see that the value of the sum gradually becomes small until the July, after that it gradually rises until the November. We know that the probability of raining gradually increases in the first half of the year nearly in most areas of China, lots of clouds after raining often exist in the sky. So the transmissivity is lower than that in the second half of the year because the weather condition will become dry and there are few clouds in the sky. Hence, the result is quite consistent with the change trend of the climate. The average values of a and b are 0.1387 and 0.6367. It is observed that the sum (0.7754) of the values for the coefficient compares well with the value (0.80) reported in literature for the mesothermal forest climate (often dry season in winner) [9]. Because most areas of China are located in the mesothermal forest climate.

From the above comparisons, everything points to the fact that Angstrom-Prescott-one parameter-model is, to a large extent, locality dependent (It is expected that the performance of any general equation will always be poor than that of the model developed for that locality.)

3. Conclusion

The present work of this paper is that a linear correlation form of Angstrom-Prescott correlations has been developed for use in estimation global radiation of China. And the model is also compared with other models (Rietveld, Ogelman et al Page) in terms of different parameters. Comparative analysis shows that the predictive accuracy of our model is far better than the rest of

the models considered in this study. Hence the monthly average daily global radiation incident on the horizontal surfaces can be estimated by the correlation developed in this paper (the error doesn’t exceed 6%). Especially for the places where there are no stations for measurements but have similar meteorological conditions in China.

4. Acknowledgment

The author is grateful to the CMA (China Meteorological Administration) for providing the data.

References

[1] T. Muneer, Solar Radiation and Daylight Models for the Energy Efficient Design of Building(Architectural

Press, Oxford,1997)

[2] S. U.UDO, Contribution to the Relationship between Solar Radiation and Sunshine duration in the Tropics:

A Case Study of Experimental Data at Ilorin, Nigeria. Turk J Phys 26(2002)

[3] JIANG Ying-ni, Models for estimating monthly mean daily Diffuse Radiation. [J]

[4] Louis E. AKPABIO, Modeling Global Solar Radiation for a tropical location: onne, Nigeria

Turk J Phys 29(2005)

[5] Chen Zhi-jun, Exporing the monthly clearness index models in china, 2005.10, Journal of Nanjing Instutude of Meteorology

[6] Louis E. AKPABIO, Relationship Between Global Solar Radiation And Sunshine Duration for Onne, Nigeria, [J] Turk J Phys 27(2003)

[7] Zhou Jin, Sunshine-based model for estimation global solar radiation in China, [J], Journal of harbin

institute of technology

[8] Lin Wenxian, Ranking the overall performance of eight sunshine-based global solar radiation models

with a nonparametric statistical procedure,[J] New Energy, 1998. 20(2). 16-19

[9] William A. Beckman, Solar engineering of thermal processes, second edition 39-40, 70-71

[10] K. J.A. Revfeim, An interpretation of the coefficients of the Angstrom equation. Solar Energy. 31,

(1983), 415