ЭНЕРГОСБЕРЕГАЮЩИЙ АСИНХРОННЫЙ ЭЛЕКТРОПРИВОД

Законы управления системой ПЧ — АД, обеспечивающие снижение потерь энергии в переходных режимах

Большой практический интерес представляет задача миними­зации потерь энергии в переходных процессах асинхронных элект­роприводов, для которых основными являются режимы пуска, торможения и реверса. Для такого типа электроприводов задача оптимального управления динамическими режимами должна ре­шаться методами математической теории оптимального управле­ния. К настоящему времени в теории частотного управления асин­хронными двигателями сформировался строго обоснованный в рамках принятых допущений подход к решению задач оптималь­ного управления динамическими режимами, в том числе и задачи управления по минимуму потерь энергии. Этот подход сочетает возможности учета основных существенных факторов поведения АД в динамических режимах и решения задач оптимального уп­равления вариационными методами.

Основные положения этой теории и некоторые результаты проведенных исследований оптимальных по минимуму потерь энергии режимов управления следующие [62].

1. Теоретическое исследование вопросов оптимального по ми­нимуму потерь энергии управления базируется на математическом описании АД как объекта управления, учитывающем электромаг­нитные переходные явления в роторных цепях и насыщение дви­гателя по главному магнитному пути.

2. При оценке качества, характеризующей энергетическую эф­фективность динамических процессов частотного управления, учитываются электрические потери энергии в обмотках статора и ротора в связи с решающим влиянием этих составляющих на энер­гетику и нагрев АД в пускотормозных режимах.

3. Задача оптимального управления по минимуму потерь энер­гии решается методом классического вариационного исчисления. Полученные решения и итоговые математические соотношения

позволяют рассчитать характеристики оптимальных процессов управления скоростью в режимах пуска и торможения АД, кото­рые могут служить эталоном для сравнения эффективности более простых законов управления.

4. На характер оптимальных процессов наиболее сильно влия­ют электромагнитные переходные явления в роторной цепи. Влия­ние эффекта насыщения двигателя по главному магнитному пути проявляется только в изменении количественных характеристик. Законы управления АД, полученные без учета насыщения магнит­ной цепи и электромагнитных явлений, неприемлемы для практи­ческого использования, так как обеспечивают низкие энергетиче­ские показатели. Законы управления, полученные только с учетом влияния электромагнитных явлений, обеспечивают достаточно близкие к предельно достижимым энергетические показатели АД.

5. Для улучшения энергетических показателей асинхронных частот- но-регулируемых электроприводов в динамических режимах целе­сообразно применять рациональное предварительное подмагничива - ние АД. Концепция многоэтапного оптимального процесса управле­ния, предполагающая формирование начального этапа подмагничи - вания, основного этапа отработки заданного изменения скорости и заключительного этапа выхода в режим установившегося движе­ния, позволяет уменьшить потери энергии и нагрев при пусках АД.

6. В связи со сложностью осуществления законов оптимального управления по минимуму потерь энергии на практике рекоменду­ются законы управления с постоянством модуля вектора токов статора и скольжения вектора токов статора или вектора потоко­сцеплений ротора при оптимальных соотношениях между ними.

Полученные с учетом насыщения законы управления, опти­мизирующие установившиеся режимы работы асинхронных дви­гателей, обеспечивают близкие к предельным энергетические по­казатели электромеханических переходных процессов.

Приведенные положения теории оптимального частотного уп­равления АД по минимуму потерь энергии носят общий характер, хотя и базируются на учете электрических потерь энергии только в одном из элементов силовой части электропривода, а именно в асинхронном двигателе. Учет электромагнитных переходных явле­ний в преобразователях частоты с непосредственной связью, с автономными инверторами тока и напряжения при решении за­дачи оптимизации не может существенно изменить качественной картины оптимальных переходных процессов по минимуму по­терь энергии, что подтверждено экспериментальными исследова­ниями реальных систем управления частотно-регулируемых элект­роприводов. Эти положения могут быть дополнены и уточнены количественными характеристиками.

Теоретическое исследование вопросов оптимального управле­ния асинхронным электроприводом с учетом электромагнитных переходных явлений и потерь энергии в преобразователе частоты представляет большие трудности в связи с нелинейностью и высо­ким порядком дифференциальных уравнений, поэтому большое значение приобретают численные методы оптимизации.

Рассмотрим один из возможных подходов приближенного ре­шения задачи оптимизации режимов частотно-регулируемого асин­хронного электропривода, учитывающего совокупность электро­магнитных явлений в двигателе и преобразователе частоты, а так­же насыщение электрической машины по главному магнитному пути. В качестве оценки эффективности функционирования асин­хронного электропривода примем суммарные электрические по­тери энергии в силовой части.

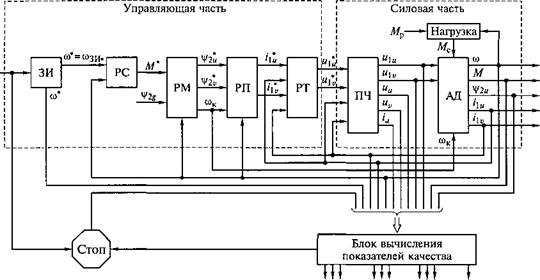
Объектом исследования является асинхронный электропривод с векторной системой автоматического управления, схема мате­матической модели которого приведена на рис. 3.57. Силовая часть электропривода имеет АД с короткозамкнутым ротором и ПЧ с автономным инвертором напряжения, получающим питание от неуправляемого выпрямителя. Силовая часть описывается уравне­ниями (2.27)...(2.30).

Система автоматического управления электропривода постро­ена по принципу подчиненного регулирования. Она имеет замкну­тые системы регулирования преобразованных токов статора, разом­кнутые системы регулирования преобразованных потокосцеплений ротора и электромагнитного момента, а также замкнутую систему регулирования скорости ротора. На входе системы регулирования скорости ротора установлен задатчик интенсивности.

Математическая модель управляющей части описывается урав­нениями регуляторов, синтез которых ведется в соответствии ме­тодикой систем подчиненного регулирования асинхронных элек­троприводов [64].

Регулятор преобразованных токов статора (РТ) представляет собой два последовательно включенных двухканальных автоном­ных регулятора пропорционально-интегрального типа. Сигналы задания iu и iv для РТ поступают с выхода регулятора преобра­зованных потокосцеплений ротора (РП) через апериодические фильтры первого порядка. Выходные сигналы ии и и ^регулятора тока являются заданиями составляющих напряжения статора. Они подаются на входы управления преобразователя частоты. Мате­матическая модель РТ с фильтрами по заданию имеет следующий вид:

27ХГ

27>/Т; + С = il

Єіи - hu ~ hu>

- iv ~hv

где Т — некомпенсированная постоянная времени по каналам и hv; крті, крТ2 и Tpji, ТРТ2 — коэффициенты усиления и постоянные времени последовательно включенных регуляторов тока.

Регулятор преобразованных потокосцеплений ротора выполня­ется в виде обращенной модели звена объекта регулирования, уравнения которой имеют следующий вид:

-Riilu = РУъ - Лад/*,;

-Rlilv = PV 2v +

¥0и — V2m ~ f-Q. oilu>

V0i> = ViL ~ LiJlv

VS =(¥£+¥o2,)1/2’ iou = V (vo)vo«;

4 = Z51 (|/o)|/o,;

•* .

hu ~ lOu ~ llui

hv ~ iov ~ iiv

Заданием для РП являются сигналы Щи = и = 0, форми­рование которых возлагается на систему регулирования электро­магнитного момента. Такое задание ориентирует результирующий вектор потокосцеплений ротора по одной из осей декартовой си­стемы координат и задает его модуль |/2 [64].

Регулятор электромагнитного момента (РМ) выполняется в виде обращенной модели звена момента асинхронного двигателя, урав­нения которого для решения задачи преобразуются к следующему виду:

Т„рМ" + М" = М•; До)к = Й2ЛГ7ч4;

= ш+дшк; v;„ = v2s; vL = о,

где Ти — постоянная времени фильтра на входе РМ.

Вход М* регулятора момента подчинен регулятору скорости ротора (PC), а вход jt2g представляет собой задание модуля векто­ра потокосцепления ротора. При решении задачи оптимизации
режимов асинхронного электропривода этот сигнал можно рас­сматривать как независимое входное воздействие. Варьируя сигна­лом |/2£, можно найти оптимальный по энергетическому крите­рию режим работы электропривода.

Регулятор скорости ротора настраивается на модульный или симметричный оптимумы в зависимости от технологических тре­бований. Например, при настройке PC на симметричный оптимум уравнения регулятора имеют следующий вид:

Тфры** + со** = со*; е*ы = со** - со*;

Щи - (^РС +

где Гф — постоянная времени фильтра на входе PC; fcPC — коэф­фициент усиления; ТРС — постоянная времени регулятора.

Для удобства анализа конечные результаты моделирования в блоке вычисления показателей качества приводятся к безразмер­ным единицам. Обратим внимание еще на одну особенность мате­матической модели системы электропривода. В ней предусмотрена операция «Стоп», которая по сигналам задания на скорость со^ и реальному сигналу скорости со выбирает время интегрирования мгно­венных электрических потерь силовой части электропривода при расчете интегральной характеристики.

Таким образом, математическая модель (см. рис. 3.57) отражает все наиболее важные при решении задачи оптимизации явления в силовой части и главные особенности структурного построения векторной системы управления асинхронным электроприводом. В такой модели независимо от заданной величины \t2g на входе регулятора момента обеспечиваются типовые переходные процессы. Следовательно, синтез оптимального управления по энергетическо­му критерию ведется при заданной форме кривой скорости, что приближает такую постановку задачи к реальной ситуации, но вместе с тем вызывает необходимость проведения большого объ­ема вычислений, вызванных учетом дополнительных факторов, присущих реальному электроприводу.

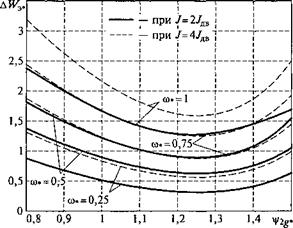
Для определения условий, обеспечивающих минимум потерь энергии за время переходного процесса, проведем численные эксперименты, заключающиеся в следующем. При фиксированных значениях параметра задатчика интенсивности ТЗИ и момента статической нагрузки Мс реактивного типа проведем серию пусков двигателя до конечной скорости со, соответствующей заданной со^, с разными значениями модуля цf2g. При этом будем фиксировать поте­ри энергии АЖЭ за период переходного процесса. На рис. 3.58 при­ведены графики относительных электрических потерь энергии A W3, при пуске АД типа 4А132М6 при разных значениях со, (шаг 0,25).

Параметр задатчика интенсивности Тзи - 1 с. Вал асинхронного двигателя нагружен реактивным моментом статического сопро­тивления Мр* = 1. Как видно на рис. 3.58, функция АЖ,, имеет экстремум.

Численный эксперимент показывает, что оптимальное потоко­сцепление |/2g, при котором потери энергии минимальны, практи­чески не зависит от конечной скорости и момента инерции электро­привода. При увеличении конечной скорости пуска экстремальная характеристика становится более острой. Оптимальное потоко­сцепление ротора на 5,4...9% превышает номинальное значение потокосцепления ротора. Эффект от оптимизации при всех значени­ях конечной скорости двигателя составляет 2...6 %.

При уменьшении параметра Тш оптимальное значение потоко­сцепления ротора увеличивается. Так, при установке Тш = 0,2 с оптимальное значение потокосцепления в относительных едини­цах равно 1,32, а эффект 5,4... 11%. Таким образом, при интенсив­ных переходных процессах пуска выигрыш от оптимизации режи­мов возрастает, что объясняется влиянием электромагнитных яв­лений в силовой части электропривода.

Практический интерес представляет оценка эффективности законов управления, полученных для насыщенного двигателя без учета электромагнитных явлений. К таким законам следует отне­сти прежде всего режим управления пуском при постоянстве мо­дуля вектора потокосцепления ротора (у2 = const) и минимуме тока статора (/j = min), которые могут быть обеспечены в системе векторного управления асинхронным электроприводом. Оценку эф­фективности режимов управления пуском проведем в рамках опи­
санной методики, что позволит сохранить единство подхода и ус­ловий численного эксперимента.

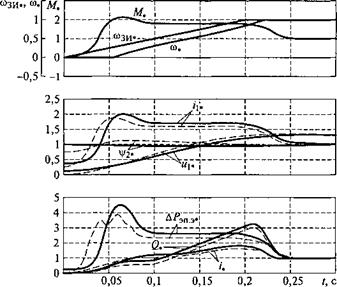
Рассмотрим сначала режим управления пуском при постоян­стве потокосцепления ротора. Значение \f2g при этом выберем, равное значению потокосцепления в номинальном режиме АД, т. е. |f2g = Угном - На рис. 3.59 приведены характеристики переход­ных процессов асинхронного электропривода с векторной систе­мой частотного управления. Параметр задатчика интенсивности Тт - = 0,2 с. Разгон двигателя осуществлялся с реактивным моментом нагрузки Мр* = 1 до скорости со* = 1. Суммарный момент инерции электропривода составлял 2/дв. Для сравнения на рис. 3.59 при­ведены осциллограммы пуска АД при постоянстве потокосцеп­ления ротора, равном оптимальному значению. Пунктирными ли­ниями показаны процессы при постоянстве потокосцепления ро­тора jf2g = |/2ном> а сплошными — при оптимальном потоко - сцеплении. Сравнение характеристик свидетельствует о том, что при одном и том же законе изменения угловой скорости АД в режиме пуска с оптимальным потокосцеплением ротора энерге­тические характеристики привода выше. В частности, электриче­ские потери энергии при пуске с оптимальным потоком ротора составили 438,8 Дж, в то время как при пуске с номинальным потоком ротора потери составили 483 Дж. Эффект от оптимиза­ции составил 10%.

При пуске двигателя в режиме минимума тока статора модуль вектора потокосцепления ротора задается в функции от электро­магнитного момента двигателя. При малых значениях момента оптимальная по минимуму тока статора зависимость корректиру­ется так, чтобы создать начальное подмагничивание машины. При численных расчетах она аппроксимируется полиноминальной функ­цией пятой степени. Искомые коэффициенты находятся методом наименьших квадратов.

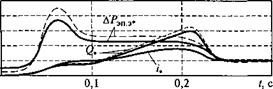
На рис. 3.60 показаны характеристики переходных процессов при пуске АД типа 4А132М6 с номинальной нагрузкой на валу двигателя. Условия численного расчета такие же, как было приведе­но выше. Пунктирными линиями показаны процессы при миниму­ме тока с подмагничиванием двигателя перед пуском, а сплошны­ми ЛИНИЯМИ — при ПОСТОЯННОМ ПОТОКОСЦЄПЛЄНИИ ротора \f2g = ¥2 ном • В обоих случаях законы изменения скорости и момента АД оста­ются неизменными и соответствуют типовым процессам управле­ния в системах подчиненного регулирования, в то время как токи и напряжения статора, потокосцепления ротора АД и другие ха­рактеристики электропривода отличаются.

Обратим внимание на то, что ток статора /1Ф, ток /. и реактив­ная мощность Q*, а также электрические потери мощности ДРЭп. э* в силовой части электропривода при пуске в режиме минимума
тока статора меньше по сравнению с режимом пуска при посто­янном потокосцеплении. Интерес представляют электрические потери энергии в силовой части электропривода в зависимости от интенсивности переходного процесса, задаваемого параметром Тш.

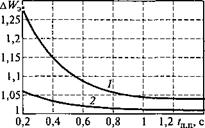
На рис. 3.61 показаны зависимости потерь энергии в режиме пуска при минимуме тока статора и постоянстве потокосцепле­ния ротора от /п п. Как видно на рис. 3.61, по интегральной харак­теристике режим пуска при постоянстве потокосцепления ротора незначительно уступает режиму пуска при минимуме тока стато­ра с предварительным подмагничиванием двигателя.

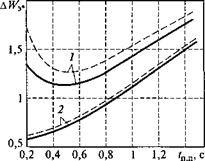
Эффект от применения режима пуска АД при минимуме тока статора возрастает с увеличением интенсивности процесса пуска, а также в электроприводах с большим суммарным моментом инер­ции. Этот вывод следует из анализа оценок эффективности режи­ма пуска АД при минимуме тока статора с начальным подмагни­чиванием, приведенных на рис. 3.62.

Полученные результаты свидетельствуют о том, что законы уп­равления пуском при минимуме тока статора и постоянстве потоко­сцепления ротора обеспечивают в целом достаточно высокие пока­затели, незначительно уступающие показателям при оптимальном управлении потоком ротора с учетом электромагнитных явлений и насыщения. Именно эти сравнительно простые с точки зрения осу­ществления законы управления находят применение в современ­ных системах автоматического управления асинхронными электро­приводами с полупроводниковыми преобразователями частоты.

Осуществление оптимальных по минимуму потерь энергии за­конов управления в принципе также возможно в системах элект-

ропривода с ориентацией по полю ротора и в системах электро­привода с управляемым абсолютным скольжением. Однако нельзя не отметить сложность их внедрения, обусловленную тем, что изменение условий работы электропривода приводит к измене­нию параметров оптимального закона управления. Таким обра­зом, степень целесообразности применения оптимальных зако­нов управления динамическими режимами будет возрастать по мере разработки практически реализуемых алгоритмов оптимального или квазиоптимального управления.