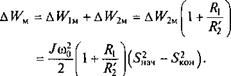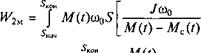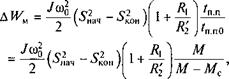ЭНЕРГОСБЕРЕГАЮЩИЙ АСИНХРОННЫЙ ЭЛЕКТРОПРИВОД

ПЕРЕХОДНЫЕ РЕЖИМЫ РАБОТЫ АСИНХРОННЫХ ЭЛЕКТРОПРИВОДОВ

2.3.1. Общие принципы оптимизации энергопотребления в переходных режимах

Переход электропривода от одного установившегося режима к другому сопровождается переходным процессом, на который за­трачивается определенное количество энергии. Эту энергию мож­

но представить в виде двух составляющих: полезной, связанной с выполнением электродвигателем определенной механической ра­боты, и потерь энергии.

Очевидно, что полезная составляющая определяется измене­нием произведения момента двигателя на его скорость. При этом в пусковых режимах, связанных с увеличением скорости двигате­ля, энергия из сети расходуется на увеличение кинетической энер­гии движущихся частей электропривода, а в тормозных, наобо­рот, кинетическая энергия движущихся частей электропривода возвращается в сеть (при рекуперативном торможении) или вы­деляется в виде потерь (при динамическом торможении или тор­можении противовключением). Полезная составляющая энергии определяется технологическим процессом и в пусковых режимах повлиять на нее не представляется возможным, а в тормозных режимах она может быть возвращена в сеть за счет рекуперативно­го торможения (разумеется, за вычетом потерь).

Потери энергии обычно делят на постоянные и переменные. Под постоянными подразумеваются потери энергии, не завися­щие от нагрузки двигателя. К ним относятся потери в стали магнито- провода двигателя, механические потери от трения в подшипни­ках и вентиляционные потери. Постоянные потери не остаются неизменными и зависят от скорости двигателя, амплитуды и часто­ты питающего его напряжения и т. д. Но так как эти потери изменя­ются в ограниченных пределах и составляют незначительную часть общих потерь, то они принимаются неизменными и равными постоянным потерям при номинальном режиме работы двигателя

Наибольший интерес с точки зрения оптимизации энергопот­ребления представляют переменные потери электропривода, кото­рые складываются из мощности потерь в меди статора и ротора двигателя:

ДРМ - ЬРм + Д^2м - + 3/2^2-

При использовании Г-образной схемы замещения (см. рис. 1.2) потери в меди статора

а суммарные потери в меди

(3.79)

Очевидно, что использование формулы (3.80) для оценки по­терь энергии за время переходного процесса затруднительно, так как для этого необходимо знать законы изменения токов двигате­ля 1Х и 1'2 в переходном процессе, а также располагать данными об изменении сопротивлений.

Более удобные расчетные соотношения могут быть получены при использовании механических переменных и параметров. Ис­пользуя известное соотношение [32] для переменных потерь в ро­торе (потерь скольжения)

= 3/22Р2 ~ M(OqS, найдем энергию потерь в роторе за время переходного процесса:

&Щи = ’j M(t)e>oS(/)dt. (3.81)

о

Потери энергии при работе электропривода без нагрузки (Мс= 0). Из уравнения механического движения электропривода при Мс = 0 получим

d/ = ^ = -^°dS.

М М

Подставив полученное значение dt в формулу (3.81) и заменив пределы интегрирования, получим

~кон

ДW2u= J A/(t)<OoS(t)

*^кон

dS = -/(о2 J SdS =

= /со2 S™H. (3.82)

Формула (3.82) более удобна для определения потерь энергии, так как для расчетов необходимо знать лишь параметры / и со0, начальное и конечное значения скольжения S.

Для примера найдем потери энергии в роторе асинхронного двигателя при его пуске, торможении и реверсе вхолостую.

При пуске двигателя SHa4 = 1, SKOH = 0, поэтому

Л^2м=^-- (3.83)

Заметим, что потери энергии в роторе в соответствии с (3.83), численно равны кинетической энергии, которая будет запасена к концу пуска в движущихся частях электропривода.

Так как при динамическом торможении 5нач = 1, - S^ = 0, то потери энергии также определяются выражением (3.83). При этом весь запас кинетической энергии электропривода превращается в потери, выделяемые в виде теплоты.

При торможении Противовключением £Нач = 2, 5К0Н = 1, а поте­ри энергии AW2m = З/соо/2, т. е. в 3 раза превышают потери при пуске и динамическом торможении и численно равны тройному запасу кинетической энергии.

При реверсе »Унач = 2, = 0, а потери энергии A W2u = 4/coq/2,

т. е. они равны сумме потерь при торможении противовключением и пуске.

Таким образом, потери энергии в роторе AW2yi за время пере­ходного процесса при Мс = 0 не зависят от времени, а определя­ются только начальным SHm и конечным SKOH значениями сколь­жения (или скорости) и суммарным моментом инерции электро­привода /.

Потери энергии зависят не только от величины изменения скольжения (5К0Н - SHa4), но и от абсолютных значений скольже­ния. Найдем потери при изменении скольжения на 0,5 при разных значениях iSHa4. Так, при »Унач = 1 и 5К0Н = 0,5 ДЖ2м= 0,75/со^/2, а при SHSL4 = 0,5 и SKон = 0 AW2м= 0,25/(Oq/2, т. е. потери энергии отличаются в 3 раза.

Представление о зависимости энергии потерь в роторе от Sm4 и *УК0Н можно получить из графиков зависимости относительных потерь в меди ротора АД от 5нач и приведенных на рис. 3.40 (относительные потери энергии даны В ДОЛЯХ ОТ величины /сОо/2, принятой за базовую АР6).

На рис. 3.40 видно, что при одном и том же изменении сколь­жения AS потери будут тем меньше, чем ближе к нулю значения б'нач И SKон. Иными словами, переходные процессы вблизи скоро­сти холостого хода связаны с меньшими потерями. Кроме того, одинаковые изменения скорости в разных направлениях приводят к разным потерям.

Из формулы (3.82) следует, что потери энергии в роторной цепи двигателя не зависят от времени переходного процесса. Это означает, что они не зависят и от формы механических характери­стик электропривода. Так, для любой из механических характери­стик асинхронного электропривода, примеры которых приведе­ны на рис. 3.41, потери энергии в роторе при одинаковых изменени­ях скорости будут равными, не зависящими от величины сопротив­ления роторной цепи. Это обстоятельство физически объясняется тем, что механическим характеристикам, для которых при дан­ной скорости моменты больше, соответствуют большие потери, но меньшая продолжительность переходных процессов.

Для определения суммарных потерь энергии в меди АД необходи­мо найти потери в меди статора. Очевидно, что AWlu = AW2mRx/R2,

Рис. 3.40. Зависимость относительных потерь в меди ротора АД от лнач и £кон

т. е. эти потери зависят от сопротивлений статорной и роторной цепей. Чем меньше сопротивление статорной цепи и больше ро­торной, тем меньше потери в статоре асинхронного двигателя.

Уменьшение потерь в статоре объясняется уменьшением пус­кового тока.

В двигателях общего назначе­ния с короткозамкнутым рото­ром обычно » Щ, т. е. в этом случае потери в меди статора и ротора примерно одинаковы.

За счет применения двигате­лей со специальной конструкци­ей короткозамкнутого ротора, имеющего повышенное сопро­тивление, потери в статоре мо­гут быть уменьшены. Например, это двигатели со сплошным стальным ротором и двигатели с повышенным номинальным скольжением краново-металлур-

гической серии. Двигатели, имеющие ротор с глубокими пазами или с двойной «беличьей клеткой», также обладают повышен­ным сопротивлением ротора, зависящим от скольжения, что при­водит к уменьшению переменных потерь в статоре.

Полные потери в меди АД

(3.84)

Для оценки суммарных потерь энергии в переходном процессе должны быть учтены рассмотренные выше постоянные потери энергии, которые будут зависеть от длительности переходного процесса, однако их учет даст более точное представление о поте­рях энергии только при чрезвычайно затянутых переходных про­цессах.

Потери энергии при работе электропривода с нагрузкой (Мс ф 0). При определении потерь энергии в меди ротора справедлива фор­мула (3.81). Для этого необходимо знать, как изменяются момент M(t) и скольжение S(/) двигателя в переходном процессе, а так­же закон изменения Mc(t).

Из уравнения движения электропривода (см. подразд. 1.3) на­ходим

Подставив полученное значение dtB формулу (3.81) и заменив пределы интегрирования, найдем

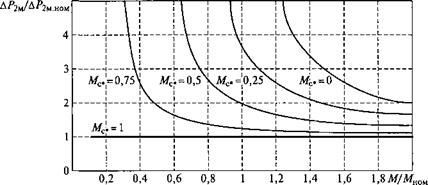
Для иллюстрации зависимости потерь в меди ротора от нагруз­ки двигателя на рис. 3.42 приведены графики относительных по­терь (в долях от /соо/2) при пуске и динамическом торможении с постоянными моментом М и моментом нагрузки Мс, которые выра­жены в относительных единицах (за базовый момент принят Мном). В соответствии с формулой (3.86) и приведенными на рис. 3.42 графиками потери энергии в роторе АД при работе под нагрузкой увеличиваются в пусковых режимах и уменьшаются в тормозных. Последнее обстоятельство связано с тем, что при торможении часть запасенной кинетической энергии расходуется на преодоле­ние момента нагрузки, поэтому в двигателе выделяется в виде потерь только оставшаяся ее часть. Потери при торможении могут быть снижены практически до нуля, если Мдв = 0. Это так называ­емый режим «выбега» двигателя, когда торможение осуществля­ется за счет Мс. Вместе с тем в пусковых режимах потери много­кратно возрастают, если момент двигателя близок к моменту на­грузки. Это связано с тем, что в данном случае динамический момент и, соответственно, ускорение двигателя очень малы и процесс пуска затягивается. Поэтому можно сделать вывод о том, что если это допустимо по технологии, то целесообразно пред­усматривать пуск двигателя вхолостую, а торможение под нагруз­кой.

Еще одну формулу для расчета потерь в меди ротора в переход­ных процессах под нагрузкой можно получить, если учесть, что по сравнению с переходными процессами при пуске АД вхоло­стую они будут отличаться временной продолжительностью. При М = const время пуска и торможения вхолостую ґп п0 = /coq/M

Время пуска и торможения под нагрузкой (снижением скоро­сти в установившемся режиме пренебрегаем) /п п = /со0/(М± Мс),

поэтому потери энергии в переходном процессе можно рассчи­тать по формуле

- SL,)^-. (3.87)

‘п. п О

Таким образом, в неуправляемых переходных процессах, когда угловая скорость о)0 задается скачком, потери энергии за время переходного процесса пропорциональны суммарному моменту инерции электропривода J, квадрату скорости идеального холо­стого хода ш0 и зависят от диапазона изменения скольжений и нагрузки электропривода.

Анализ формул (3.82) и (3.86) позволяет назвать два основных способа снижения потерь энергии в переходных режимах:

1) уменьшение суммарного момента инерции электропривода /;

2) регулирование в переходных процессах скорости идеально­го холостого хода, т. е. использование управляемых переходных процессов.

Особенно эффективны эти способы для электроприводов с частыми пусками и торможениями (кранов, лифтов, манипуля­торов, рольгангов, экскаваторов и т. д.).

Имеются следующие способы уменьшения момента инерции электропривода.

1. Использование малоинерционных двигателей.

2. Рациональное конструирование механической передачи (вы­бор оптимального передаточного числа редуктора [28], оптималь­ных массогабаритных показателей механической передачи и т. д.).

3. Замена одного двигателя двумя и более с сохранением суммар­ной мощности. Как правило, суммарный момент инерции двух двигателей половинной мощности оказывается меньше момента инерции одного двигателя полной мощности в рамках одной се­рии двигателей.

Регулирование скорости идеального холостого хода осущест­вляется следующими способами: изменением числа пар полюсов в многоскоростном АД или изменением частоты питающего на­пряжения в системе ППЧ—АД.

Рассмотрим процесс пуска двухскоростного АД. Допустим, что путем переключения обмоток статора при пуске можно в 2 раза увеличить число пар полюсов, т. е. в 2 раза уменьшить скорость идеального холостого хода, снизив ее до О,5(о0. При этом потери за время пуска вхолостую до скорости О,5со0 (5нач = 1; SK0H = 0) со­ставят АЖ2м(1) = /(0,5со0)2/2 = /со02/8-

На втором участке пуска от 0,5соо до щ переключением обмоток синхронная скорость увеличивается до со0, £нач = 0,5; 5К0Н = 0 и поте­ри составят

Д^2„(2, =^(0,52-0) = /0)^/8.

Суммарные потери в меди ротора за время ступенчатого пуска составят

“ Д^2м(1) + Д^2м(2) /4,

что в 2 раза меньше, чем при прямом пуске.

В общем случае, если скорость идеального холостого хода в переходном процессе имеет п одинаковых ступеней регулирова­ния, потери энергии в роторе также уменьшаются в п раз, т. е.

Можно показать, что потери снижаются и при ступенчатом торможении. Так, при динамическом торможении в две ступени потери энергии уменьшатся в 2 раза, а при торможении противо- включением переход на пониженную скорость дополнительно сопровождается рекуперацией энергии в сеть и суммарные потери в роторе уменьшатся в 1,5 раза.

Следует, однако, иметь в виду, что момент инерции много­скоростного двигателя значительно выше момента инерции одно­скоростного двигателя с той же мощностью и номинальной ско­ростью вращения, поэтому замена односкоростного двигателя мно­госкоростным только для уменьшения потерь энергии представ­ляется нецелесообразной. Можно говорить только о сравнении прямого и ступенчатого пуска для одного и того же многоскорост­ного асинхронного двигателя.

Еще более эффективным путем снижения потерь является непре­рывное управление скоростью идеального холостого хода путем из­менения частоты питающего АД напряжения в системе ППЧ—АД.

Построим переходный процесс пуска АД вхолостую при изме­нении частоты напряжения на статоре так, чтобы сформировать закон изменения скорости идеального холостого хода в виде [32]:

= «онач + Et

"О (0 = ^0 ном

НОМ

При 0)0 < СОоном; При Wq — Wqhomj

где є — ускорение электропривода, обеспечивающее заданное вре­мя переходного процесса /п п = /(О0н0м/^при постоянном момен­те двигателя М, є = dw/dt = со0Н0МЛп. п-

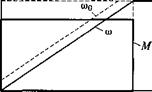
На рис. 3.43 показаны графики переходных характеристик при частотном пуске АД вхолостую.

При постоянном моменте М, выбранном исходя из допусти­мого ускорения или по перегрузочной способности двигателя или преобразователя, такое управление обеспечивает в меди ротора потери энергии:

(3.88)

Эти потери по сравнению с прямым пуском снижаются про­порционально 2(ОоначМ)ном - В за­висимости от мощности и типа двигателя потери могут умень­шиться в 5 —10 раз.

При определении полных по­терь энергии за время переход­ного процесса асинхронного

Рис. 3.43. Переходные характеристики двигателя необходимо учиты - при частотном пуске АД вхолостую вать, что к переменным поте-

рям относятся и потери в меди

статора. С учетом (3.84) потери энергии в меди АД (переменные потери) составят

(3.89)

а суммарные потери в двигателе с учетом постоянных потерь со­ставят

A Wm = AWM +(АРС + ДРмех)/п. п.

Разумеется, выражения (3.89) и (3.90) являются оценочными, так как получены при определенных допущениях. Тем не менее с их помощью можно при проектировании и модернизации асин­хронного электропривода выбирать такие технические решения, которые обеспечивают минимизацию потерь энергии в динами­ческих режимах работы электропривода.