ЭНЕРГОСБЕРЕГАЮЩИЙ АСИНХРОННЫЙ ЭЛЕКТРОПРИВОД

Математическое описание элементов силовой части ППЧ—АД

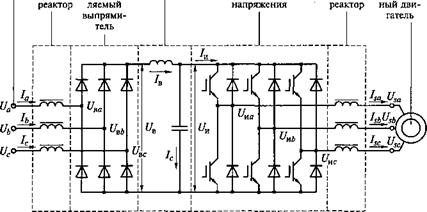
Рассмотрим математическую модель типичной системы ПЧ — АД, схема силовых цепей которой представлена на рис. 2.8. В со­став системы ПЧ—АД входят трехфазный мостовой АИН с ШИМ выходного напряжения и короткозамкнутый асинхронный двига­тель. Источником напряжения для АИН служит неуправляемый выпрямитель с коммутирующим реактором на входе и L С-фильт­ром на выходе. Обмотка статора двигателя соединена в звезду и подключена через реактор к выходу инвертора по схеме без нуле­вого провода.

При составлении математической модели силовой части ПЧ— АД будем использовать метод структурного моделирования, вы­делив в качестве отдельных элементов АД, АИН с выходным ре­актором и неуправляемый выпрямитель с входным коммутиру­ющим реактором и £С-фильтром на выходе.

Уравнения асинхронного двигателя. В качестве исходной модели асинхронного двигателя с короткозамкнутым ротором примем сле­дующую систему скалярных уравнений:

где uXu, ulv, ilu, ilv, ц/1и, j/It, — соответственно преобразованные напряжения, токи и полные потокосцепления обмотки статора; hu* hm V2Ui V2v — преобразованные токи и полные потокосцепле­ния обмотки ротора; /0н, i0v, v|/0u, |/0„ — результирующие токи намагничивания и главные потокосцепления.

Напомним, что насыщение магнитной цепи машины в модели АД учитывается с помощью переменного коэффициента L0, за­висящего от тока намагничивания и определяемого зависимостью Lq = L0(i0), где /0 — модуль результирующего вектора намагничи­вающих токов, /0 = (/о„ + Для линейной магнитной цепи

коэффициент L0 является постоянной величиной.

Уравнения инвертора напряжения. Автономный инвертор напря­жения с ШИМ представляет собой сложное нелинейное дискрет­ное устройство. Несущая частота АИН на полупроводниковых при­борах составляет 2... 16 кГц. При таком высоком уровне несущей частоты для построения математических моделей АИН использу­ется метод выделения полезных сигналов путем усреднения мгно­венных значений переменных в пределах периода несущей часто­ты. В этом случае инвертор напряжения с симметричной двухсто­ронней ШИМ во вращающейся прямоугольной системе коорди­нат описывается следующей системой уравнений:

где и*и, u*v — преобразованные задающие воздействия; /„, fv — усредненные коммутационные функции; U0 — амплитуда опорного сигнала; ии — напряжение источника питания инвертора; /и — усредненный ток питания инвертора; uMU, uHV — усредненные вы­ходные напряжения инвертора; ilu, iXv — усредненные выходные токи инвертора.

Выходные реакторы моделируются уравнениями:

Phu ~ ^р! вых(^ии + ^К^р. ВЬІХ^ІУ ^р. ВЬІХ^ІИ ^1«)?

piv — Lp bblx(llHV — COKZp ВЬІХ/іи — Rp. vuxhv ~ Uv)>

где /?р. вых, Хр. вых — активное сопротивление и индуктивность вы­ходного реактора.

Уравнения неуправляемого выпрямителя. Для учета главных осо­бенностей неуправляемого выпрямителя при анализе энергети­ческих характеристик системы ПЧ—АД в переходных и устано­вившихся режимах воспользуемся математической моделью, учи­тывающей только основную гармонику коммутационной функ­ции выпрямителя. В прямоугольной системе координат, враща­ющейся с произвольной угловой скоростью о)к, непрерывная мо­дель неуправляемого выпрямителя с входным реактором может быть представлена следующей системой уравнений:

Uu — Uru Lp BXpiu — (J)KLp BX/V + ^р. вх^і/j Mv ~ Mbv -^p. BxP^v ^к-^р. вх^м Rp. Bx^v^

Ли = —COS(0, -0K);

71

, 2-J3 . „ . (2.30)

/,„ = sin(0, -eK);

n

Mb ~ ^ і}^ви/ви Mbv/bv ) >

Іи ~ Ів/виі iv ~ ^b/bv)

= P® К 5

где uu, uv, iu, iv — преобразованные основные гармоники напряже­ний и токов сети; uBU, uBV— преобразованные основные гармони­ки напряжений на силовом входе неуправляемого выпрямителя; /еш> Ibv — преобразованные основные гармоники коммутацион­ных функций неуправляемого выпрямителя; 0, — угол поворота обобщенного вектора коммутационной функции выпрямителя, или результирующего вектора тока сети, относительно оси фазы А напряжения сети; 0К — угол поворота системы координат; ив, /в — напряжение и ток на выходе выпрямителя; Rp вх, LpBX — активное сопротивление и индуктивность входного реактора.

Уравнения для фильтра звена постоянного тока. Модель ZC-филь - тра на выходе неуправляемого выпрямителя описывается линей­ными уравнениями:

рів = £р! ф(Ив ~ ^р. ф^в —

рии — С g. ф/с5 (2.31)

= *В “ ^И)

где Рр ф, Ьр ф — активное сопротивление и индуктивность сглажи­вающего реактора LC-фильтра; Сбф — емкость конденсаторной батареи фильтра; /с — ток конденсатора фильтра.