Разработка и построение алгоритма модели
На первом этапе необходимо получить основные данные по геометрии поровой структуры.
Наиболее точным способом получения геометрических данных поровой структуры является прямой метод измерений структурных элементов системы на микроснимках и последующая их статистическая обработка. Получение снимков с помощью современного микроскопического оборудования и последующая их обработка в программах с функциями автоматического проектирования позволяет успешно решить эту трудоемкую задачу.
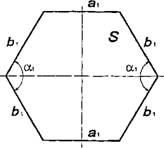
На площади среза S0 необходимо определить следующие геометрические данные каждой ячейки:
• максимальные линейные размеры ячейки по двум взаимно перпендикулярным направлениям D\ „ D±,;
• площадь ячейки S,.
В случаях когда прослеживается явная направленность поровой структуры, значения £>ц „ Dx необходимо определять с ее учетом (параллельно и перпендикулярно наибольшим граням ячейки).
Площадь S0 и количество срезов определяется исходя из поставленной задачи.
На втором этапе по полученным средним значениям D\, D.L, S всех ячеек рассмотренного участка (среза) производится построение ГСЭ.
При построении ГСЭ за форму усредненной ячейки необходимо принимать форму додекаэдра в объеме или шестиугольника на плоскости, а их геометрические размеры определять исходя из средних значений полученных прямых измерений. Принятая форма ячейки предпочтительна ввиду того, что она ближе всего отражает реальную пористую систему различных пенопла - стов [13], а также из-за высокой изотропности ячейки по теплопроводности в форме правильного шестиугольника.
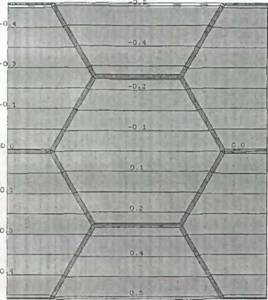
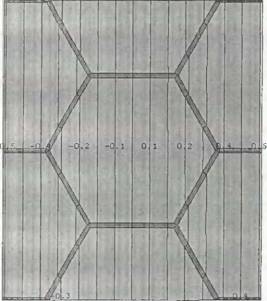
На рис. 3.1 представлены результаты теплотехнических расчетов (в виде изотерм и распределений плотностей тепловых потоков) модели ячейки в форме правильного шестиугольника со стороной 0,2 мм и толщиной стенки поры 1 мкм по двум взаимноперпендикулярным направлениям при прочих равных условиях в программе THERM (принятый масштаб построения 1000 : 1). Исходные расчетные данные и результаты расчетов представлены в табл. 3.2 и 3.3 соответственно.
Таблица 3.2
|
Наименование параметра |
Значение параметра |
|
Теплопроводность твердой фазы, Вт/м-°С |
0,199 |
|
Теплопроводность газообразной фазы, Вт/м-°С |
0,032 |
|
Граничные температуры т^ г, °С |
-0,5 ; + 0,5 |
|
|
|
|
|
-О. 0.0 0.1 0.3
|
6
|
|
|
Газообразная фаза |
|
1 |
|
Твердая фаза |
Повышение теплового потока
Рис. 3.1. Изотропия теплопроводности ячейки в форме правильного шестиугольника по результатам расчета в программе THERM: а. в - расчетная модель с полученными изотермами; б, г - распределение плотностей теплового потока по модели
|
Таблица 3.3
|
Таким образом, расчетом определена изотропия по теплопроводности модели ячейки в форме правильного шестиугольника для исходных расчетных значений газонаполненных полимеров.
За форму усредненной ячейки модели принят шестиугольник (при моделировании на плоскости) с габаритными размерами £>ц, Z)x и площадью S.
Далее исходя из геометрии рассмотренных усредненных ячеек определяются размеры ГСЭ.
|
(3.3) |
Необходимые геометрические данные для построения ГСЭ (рис. 3.2) можно найти по следующим формулам:
25 п
А2 =——D,„
|
(А/ ~ а2 )2 |
|
(3.4) |
B2=J(b/2)2
С — а2 + DЦ.
Толщина полимерных стенок (перегородок) h ГСЭ определяется по параметру газонаполненности G:
H = (-G)-Sgse/l, (3.6)
Где Sgse - площадь ГСЭ, м2; / - суммарная длина всех полимерных перегородок, входящих в ГСЭ, м.
|
(3.5) |
Общий алгоритм построения ГСЭ представлен на рис. 3.2.
|
Л / Ьг/ /<Х7 |
S! 062 (S |
|
|
V |
/ь* Зз / |
|
|
0п |
||
V
D її
Mi 2
|
Л |
|||
|
1 |
/ |
К |
І |
|
At 2 |
1 Л Эг • |
|
H ^r |
Рис. 3.2. Алгоритм построения ГСЭ
На третьем этапе выполняется построение модели полученного ГСЭ каждого рассмотренного участка (среза) в компьютерной программе по расчету температурных полей методом конечных элементов (в требуемом масштабе согласно возможностям программы).
Далее необходимо определить и задать значения характеристик материалов, входящих в построенную модель:
• коэффициент теплопроводности твердой фазы? ч, исходя из вида используемого полимерного сырья;
• эквивалентный коэффициент теплопроводности газообразной фазы Xg, Исходя из D\ и Dx полученной усредненной ячейки и вида заполняющего ее газа для конкретной температуры Т.
В завершение в программе для построения модели задаются граничные условия 3-го рода согласно поставленной задаче и производится расчет тепловых потоков, по результатам которого определяется А. ф.
|
|
Перед выполнением расчета необходимо произвести разбивку построенной в программе модели на КЭ. В настоящее время большинство совре-
При использовании программа THERM результатом расчета является распределение температур по всей площади модели и коэффициент теплопередачи, Г10 которому определяем искомую величину Хф
|
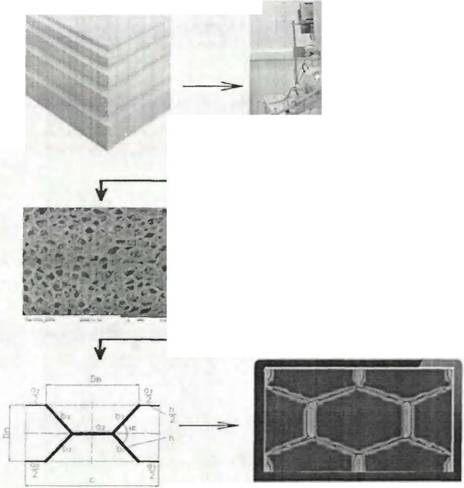
Рис. 3.3. Этапы построения структурной модели газонаполненного полимера |
Основные этапы построения модели поровой структуры в виде схемы представлены на рис. 3.3.
|
|
|
О о Шй Q;0 І о ^ ZU CD 'й С' F > О ЛЭ L-O "5> (О ю'О . _ —I—і J---------- І-.ІЛ-Т-i~..uL |
При сложной макроструктуре материала, например, при наличии нескольких видов пор, геометрические размеры которых отличаются друг от друга на несколько порядков (например, для ПСБ), построение модели необходимо проводить в 2 этапа. Сначала рассматриваются участки материала с более мелкими порами, для которых производится построение модели и рассчитывается значение Хф. На втором этапе производится моделирование крупнопористой системы с заменой участков, рассмотренных на первом этапе, на однородный материал с коэффициентом теплопроводности Хф.
Несмотря на то, что разработка модели производилась на примере экструзионного пенополистирола, её можно использовать для любых газонаполненных ячеистых полимеров ввиду аналогии.
Представленная разработка позволяет определять изменение теплопроводности при моделировании поровой структуры с различными видами газов и материалов твердой фазы. Таким образом, при наличии данных по изменению Xg и Xs исследуемого материала с течением времени (в процессе эксплуатации) можно прогнозировать и изменение Хф