Двигатели стирлинга

Условия балансировки ромбического механизма привода

Ромбический приводной механизм, бывший некогда одним из основных механизмов привода двигателя Стирлинга, сейчас вышел из употребления и применяется лишь в очень редких случаях. Однако он должен вернуться, если окажутся жизнеспособными корабель­ные двигатели Стирлинга. Кроме того, ромбический привод применим не только для двигателей Стирлинга, поскольку он является прос­то механизмом, преобразую­щим поступательное движе­ние во вращательное при полной балансировке. К то­му же этот механизм являет­ся наглядным учебным по­собием для студентов техни­ческих вузов. Ввиду уни­кальности ромбической си­стемы привода рассмотрим ее, чтобы читатель смог оце­нить ее потенциальные дина­мические свойства, а будущий конструктор смог правильно спро­ектировать такую систему.

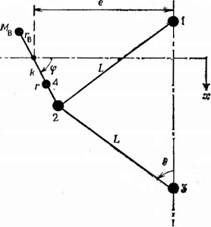
Из схемы, представленной на рис. Б.1, находим координаты точек 1—4:

Xt = Г sin ф — L cos 6, х2 = г$шф, (Б.1)

Х3~ г sin ф L cos 0, x4 = &sin^>, (Б.2)

А также sin 0 = (е — г cos ф)/Ь. Следовательно, L cos 0 = [L2 — (е — г cos ^>)2]"2. Обычно это выражение разлагают в ряд с помощью теоремы бинома, но здесь мы имеем возможность применить разложение в ряд Фурье. Поскольку рассматриваемая функция содержит

29 Зак. 839
только косинусоидальные слагаемые, говорят, что функция чет­ная и ряд Фурье будет содержать только косинусоидальные члены. Следовательно,

Оо

L cos6=Ј Ап cosпф,

П=0

И тогда

= Г sin ^Ь — А„ cos Пф, (Б. З)

П=0

Х3 = г sin Ф - f Y. АП C«S пф. (Б.4)

И -0

Если дважды продифференцировать соотношения (Б.1) — (Б.4) и умножить полученные выражения на соответствующие массы от Mi до М4, то можно найти соотношения для баланса сил:

М. х{ = Мх | ф2 г sin Ф + £ п2Ап cos Пф^ +

TOC o "1-3" h z + ф(г cos ф + J пА„ cos пф) |, (Б.5)

M2x2 = Л42 [— <Ј2r sin Ф + <fr cos (Б.6)

М3х3 = М3ф2 г sin Ф—Yj п2Ап cos пф^ +

+ <f (г cos Ф — YJ tiAn cos л^ j, (Б.7)

М4хл = AJ4 [— Ftk sin Ф + ФИ cos Ф]. (Б.8)

Чтобы не возникло «разбалансирующих» сил инерции, сумма соотношений (Б.5) — (Б.8) должна равняться нулю. Рассматри­вая эти соотношения, нетрудно заметить, что имеются члены, со­держащие низшие гармоники скорости вращения кривошипа, и члены, содержащие высшие гармоники, которые нужно сумми­ровать до бесконечности.

Для балансировки сил по низшим гармоникам рассмотрим выражение, следующее из приведенных выше соотношений при П = 1:

- Ф2 {[(М, + M2 + M3)r + M,k] sin Ф + MBrB sin (ф + QB)} + + ^{[(М, + М2 + М3)г + cosФ + Мвгвсоз(ф + 6В)} = О, (Б.9)

Где Мв — балансировочная масса, расположенная в точке с ра­диальной координатой гв и угловой координатой вв.

Если балансировочная масса расположена в точке с угловой координатой 0в = л, двигатель будет уравновешен при номи­нальной скорости вращения коленчатого вала, когда

(М, + M2 + M3)r + M<k = Мвгв. (П. 10)

Это выражение дает первое условие балансировки. Обращаясь теперь к балансировке по высшим гармоникам и рассматривая соответствующий баланс сил, полученный после суммирования соотношений (Б.5) — (Б.8), находим

Оо оо

¥п2 Е An Cos Пф (М, — Л? з) + фп% I4„Cos Пф (М,-М3)=0. (П. 11)

П=2 п=2

Единственная величина в левой части уравнения (Б.11), кото рая может обращаться в нуль, — это Л4,—Мл. Чтобы сбаланси­ровать высшие гармоники, нужно выполнить условие

М{ — М3 = 0, или Mi = M3. (БЛ 2)

Чтобы добиться идеальной балансировки всей системы, необхо­димо учесть влияние сил, создаваемых соединительными рыча­гами. Считая, что массы соединительных рычагов сосредоточенм в их центрах тяжести, переписываем соотношение (Б. 10) в вп ie

Мвгв = г [0,5 (Мр + Md) + Мрс + Mdc] + Mcpk. (Б. 1 3)

Для полной балансировки системы привода следует одновре­менно удовлетворить условиям (Б. 12) и (Б. 13).

ОБОЗНАЧЕНИЯ

Mi — масса рабочего поршня, его штока н части шатуна, участвующей в возвратно-поступа­тельном движении; Мч — масса вращающихся частей шатуна рабоче­го поршня и шатуна вытеснительшч о поршня;

М3 — масса вытеснительного поршня, его штока и части шатуна, участвующей в возвратно - поступательном движении; УИ4 — масса кривошипа, действующая на радиу­се k

MB — балансировочная масса, расположенная и точке с радиальной координатой гв и угло­вой координатой ф+ 0в; Ф — угол поворота кривошипа; L — длина шатуна;

Е — эксцентриситет приводного механизма; г — радиус кривошипа.