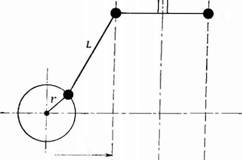
Ромбический приводной механизм (рис. 2.37)
Рассматривая двигатели Стирлинга, модификация которых отлична от модификации альфа, необходимо помнить, что движение поршня в полости сжатия нельзя связать с изменением 'Объема этой полости, просто умножив перемещение поршня на
площадь его сечения, поскольку полость сжатия образуется при встречном движении рабочего и вытеснительного поршней. Полностью соотношения, определяющие изменение объема, приведены в диссертации Мейера [49]; мы предлагаем лишь итоговые формы этих соотношений. Получаются два различных соотношения в отличие от случая кривошипно-шатунной системы,
|
Рис. 2.37. Ромбический приводной механизм. [Тжсцентри - ситет |
Когда требуется лишь замена ф на ф — а Эти соотношения имеют вид
УЕ (ф) = RAd {sin ф 4- [т2 -(е - Cos ф)2]0-5 — [(т— 1)2-е2р} (2.78) Vc (ф) = 2ГАр {[т2 - (е — I)2]0-5 - [Т2 - (е - cos ^)2]0-5}, (2.79)
Где M = R/L, е — отношение эксцентриситета к радиусу кривошипа.
|
(2.80) |
Чтобы провести гармонический аналнз, необходимо разложить в ряд член [т2 — (е — cos^>)2]°>5. Это можно сделать различными способами [57], но разложение в ряд Фурье позволяет получить наибольшую информацию. Ряд Фурье записывается в форме
Оэ
[т2 — (е — cos ф)2]0-5 = £ В,- cos }ф,
Где Bj — коэффициенты Фурье, определяемые обычным образом. Значения Bj для различных комбинаций т и е приведены в приложении 2 работы [49]. Используя этот ряд для случая
равных диаметров рабочего и вытеснительного поршней, получаем
VE (Ф) = RAd [с + D cos (ф - W) + Е В, cos }ф, (2.81)
Vc (Ф) — г (Ad — Ar) [Е - F cos ф - 2 Д В, cos , (2.82)
Где С = В0 — т~1 [(1 — M)2 - M2F D = (BI + О"'5, Arctg (V), Е = (2/m) [1 - т2(е - I)2]0-5, F = 2В,.
|
I t ■ • ! I ' ' д I I 1 1 I I I I I О 100 200 300 ЗБО Угол поворота кривошипа, грай |
|
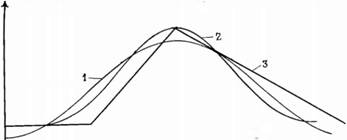
Рис. 2.38. Сравнение изменений объема при идеальном, синусоидальном и реальном движениях поршня (ромбический приводной механизм). 1 — первая гармоника; 2—реальное движение; 3—прерывистое движение.
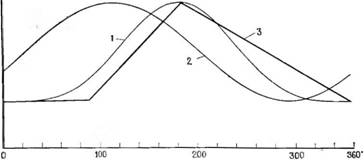
Угол поворота кривошипа f грай Рнс. 2.39. Сравнение изменения объема, рассчитанного по соотношению (2.75), с реальным значением (ромбический приводной механизм). I—реальное движение; 2—синусоидальное движение; 3—прерывистое движение. |
19 Зак. 839
Если, например, т — Ъ и е = 1, то В0 = 4,8453, ВI = 0,2075, В2 = —0,0538, Вз = 0,0012 и т. д. Подставив эти значения в соотношение (2.81), находим, что практически точное значение реального изменения объема можно получить, используя лишь первые члены ряда до второй гармоники включительно.
Использование первой гармоники, т. е. приближения синусоидального движения, неудовлетворительно [57, 58], а выражение типа (2.75), полученное в приближении синусоидального изменения рабочего объема, дает еще менее точные результаты, как это видно из рис. 2.38 и 2.39. Здесь также отчетливо видно отклонение от идеального случая.