Приводной механизм с косой шайбой
|
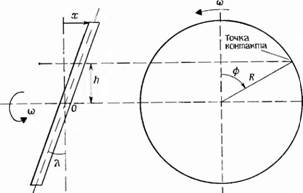
Рис. 2.40. Кинематика косой шайбы с точкой контакта. |
|
/ |
|
(2.83) |
|
Движение происходит в трех плоскостях. Лишь в очень немногих работах дается вывод соответствувщих уравнений, поэтому мы приведем здесь некоторые подробности. Вначале рассмотрим точку контакта в положении, где соединительный шток касается плоскости поверхности косой шайбы. Эта точка вследствие вращения вала описывает окружность, как показано на рисунке. Величина перемещения х выражается формулой X — Xq xfay |
На рис. 2.40 представлена схема основного приводного механизма с косой шайбой. Кинематический анализ этого механизма привода сложнее, чем других механизмов, поскольку
но Xh — HtgK, H — R cos ф; следовательно, х0 — R tg К (поскольку в положении 01 h=R), а
Xfr = R tg % cos Ф, (2.84)
И тогда
X — R tg Я (1 — cos ф).
Длина хода поршня SL равна 2х, а рабочий объем Vs равен произведению 2х на площадь сечения поршня. Следовательно,
У(ф)=-^-(1-с08ф). (2.85)
Итак, предположение о синусоидальном изменении объема является абсолютно правильным. Параметр Xh определяет положение поршня в полости, и если дважды продифференцировать соотношение (2.84), то можно найти ускорение:
Xh — — С02Л
Это выражение определяет простое гармоническое движение. Соотношения для изменения объема зависят от типа контакта
|
|
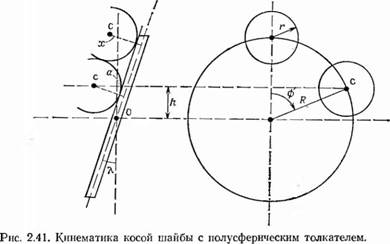
С поверхностью косой шайбы, профиля поверхности и скорости изменения угла поворота кривошипа. Полное описание расчетных методик для многочисленных возможных вариантов можно найти в работах, посвященных конструкции кулачковых систем, например в работе [59]. До сих пор, рассматривая применение приводного механизма с косой шайбой в двигателе Стирлинга, мы предполагали, что профиль поверхности контакта между штоком и шайбой образуется поверхностью шайбы. В разработанных фирмами «Форд» — «Филипс» и «Дженерал моторе» — «Филипс» двигателях, имеющих приводной механизм с косой шайбой, использовались кулачковые элементы конструкции типа полусферического толкателя; в этом случае расчетные соотношения несколько изменяются [60]; схема общей системы представлена на рис. 2.41. Теперь применимо соотношение
*h + а — r/cos ^ (a = htgl)
И параметр Xh выражается формулой
Xh = r/cos К — R tg % cos Ф. (2.86)
Следовательно, движение все еще остается синусоидальным и подчиняется законам простого гармонического движения, так как величина r/cos Я постоянна.