Двигатели стирлинга

Общие замечания

Из двух описанных методов, несомненно, предпочтительнее с аналитической точки зрения метод характеристик, но он не­сколько сложнее и требует значительно более высокой квали­фикации исследователя. Метод узлов подробнее разработан применительно к двигателю Стирлинга и вполне приемлем при низких и средних скоростях, но при высоких скоростях необ­ходимо учитывать распространение волн давления конечной амплитуды, что пока не позволяет применить метод узлов в по­следнем случае. Кроме того, из-за предположения о постоян­стве параметров внутри ячеек невозможно проследить за траек­ториями отдельных частиц, а это необходимо для понимания взаимосвязи между различными механизмами течения и тепло­обмена.

В настоящей главе выведены уравнения, описывающие об­щее нестационарное течение рабочего тела в канале. Если рас­сматривать рабочие полости переменного объема, то в уравне­нии энергии нужно учесть еще один член, выражающий перенос работы, а именно dW/dt Кроме того, можно пренебречь членом, выражающим потенциальную энергию, который мал по сравне­нию с другими членами. Обычно пренебрегают кинетической энергией, а в некоторых случаях и количеством движения газа [20, 55]. Использование этих предположений может, видимо, привести к серьезным погрешностям для высокоскоростных дви­гателей, но ввиду отсутствия экспериментальных данных нельзя сделать каких-либо определенных выводов по этому вопросу. Хотя такие предположения позволяют резко сократить затраты машинного времени, уровень и строгость анализа должны сни­зиться. Некоторые исследователи применяют новый подход, при котором на некоторых стадиях решения пренебрегают различ­ными эффектами, но в конце концов учитывают их. Например, сначала уравнения можно решить, пренебрегая аэродинамиче­ским сопротивлением (и, следовательно, количеством движения) и кинетической энергией, затем включить в рассмотрение один из членов, которыми ранее пренебрегалось, и вновь решить уравнения с более точными начальными условиями, а в конце концов учесть все эффекты. Применение такого подхода позво­ляет на порядок снизить затраты машинного времени.

Последнее замечание следует сделать относительно выбора координат. В предложенных к настоящему времени методах комбинированного анализа используется система координат Эй­лера (x,t), поскольку она применяется при рассмотрении кон­трольного объема. Можно применять и другие системы коорди­нат, а именно лагранжевы и псевдолагранжевы. Если сравни­вать с этими двумя системами, то использование эйлеровых координат приводит к более громоздким расчетам при анализе одномерного нестационарного течения [66]. Как будет. показано ниже, метод характеристик и метод узлов на самом деле свя­зывают подходы Эйлера и Лагранжа, и связывающее соотно­шение можно найти, исходя из понятия поля параметров. Од­нако в данный момент мы определим различные координаты для одномерной системы. В рамках подхода Эйлера рассмат­ривается постоянный объем в пространстве, и параметры рабо­чего тела, мгновенно занимающего этот объем, определяются таким образом, что нет необходимости следить за отдельными частицами газа. При использовании подхода Лагранжа рас­сматриваются отдельные частицы и прослеживаются их траек­тории в поле течения. В одномерной системе рассматривается слой газа (а не отдельные частицы) и переменная х заменяется другим параметром (скажем, а для данного слоя газа), который равен величине х при t — 0, и, следовательно, значение а будет изменяться от частицы (слоя) к частице (слою). Псевдолагран - жева координата т данного слоя газа обозначает массу газа, содержащегося в объеме между этим слоем и исходным слоем при t = 0, и поэтому каждый слой имеет свое значение т, ко­торое остается постоянным [67]. В псевдолагранжевых коор­динатах основные уравнения сохранения выражаются в очень простой форме. Читателям, интересующимся этим математиче­ским вопросом, рекомендуем обратиться к монографии Куранта и Фридрихса [50], где подробно рассматриваются различные системы координат. В этой монографии не используется термин «псевдолагранжевы координаты», хотя в работах [66, 67] он применяется. Рассматриваемый вопрос освещается в моногра­фии Куранта и Фридрихса [50, гл. 18].

Ч

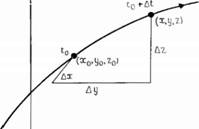
Рис. 3.6. Лагранжсво поле параметров в прямоугольной системе координат.

Кратко рассмотрим понятие поля параметров. При анализе задач гидромеханики удобно определять параметры движущейся жидкости в зависимости от пространственных координат, и, сле­довательно, поле параметров определено, если в каждой точке пространства, занятого течением, известны значения этих пара­метров. Таким образом, например, функция p(x,y,z,t) опреде­ляет давление в точке Q(x, У, z) для частицы жидкости, по­падающей в эту точку в момент времени t. В лагранжевых координатах давление отдельной частицы j определяется функ­цией pj-pi(t). Другими словами, при подходе Лагранжа не требуется задавать фиксированную систему координат, как при подходе Эйлера, поскольку система координат движется вместе с частицей. Основные законы движения жидкости справедливы только для системы, имеющей постоянную массу, как в подходе Лагранжа, но они выражаются в фиксированной системе ко­ординат, как в подходе Эйлера. Поэтому необходимо найти со­отношение, связывающее оба этих подхода, и это соотношение можно получить, применяя понятие «субстанциональная произ­водная». Рассмотрим представленные на рис. 3.6 положения ча­стицы в поле течения в моменты времени t \ t At. Найдем изменение какого-либо параметра частицы, скажем давления; при использовании подхода Лагранжа изменение р за время At Определяется формулой

Ap = p(t + At)-p(t). (3.92)

Применяя обычную теорию пределов, находим диапазон изме­нения р:

Игл P(' + AQ-Pt') . (3.93)

At ->0 Ы dt Jt v

Б эйлеровой системе Р = p(x, y,z, t) и x — x(t), y = y(t), z = — z(t) для лагранжева пространства. Следовательно,

>=+Ш *+(£),*+($■),* <м«>

И скорости изменения отдельных координат х, у, z, t можно найти так же, как скорость изменения Ар. Например,

Л'лГо (49=1=^)- (з-95)

Тогда скорость изменения давления выражается соотношением

Это соотношение равносильно соотношению (3.94), что позво­ляет установить связь между изменениями по Лагранжу (левая часть уравнения) и по Эйлеру (правая часть уравнення). Чтобы подчеркнуть эту связь, производную, стоящую в левой части уравнения, обычно обозначают D( )/Dt и называют субстан­циональной производной. В одномерном случае получаем

ОО _ао (3.97)

Dt dt 1 дх

Первый член в правой части уравнения называется локальной производной, а второй член - - конвективной производной.

Читателям, желающим освоить усовершенствованные методы анализа рабочего процесса, происходящего в двигателе Стир­линга, следует очень внимательно отнестись к соотношению (3.97), поскольку изучение имеющихся методов показало, что часто не делают различия между производными д/dt и D/Dt, А также одновременно применяют подходы Лагранжа и Эйлера без учета связи между ними.

Лагранжевы и псевдолагранжевы координаты имеют пре­имущество перед эйлеровыми в случае одномерной по простран­ству задачи. Когда же решается задача о течении, зависящем от двух и более пространственных координат, трудности, свя­занные с определением траекторий громадного количества от­дельных частиц, становятся математически непреодолимыми, и следует отдать предпочтение подходу Эйлера. Для одномерной по пространству системы подход Лагранжа имеет явное пре­имущество, поскольку помимо того, что он позволяет проследить за движением отдельных слоев рабочего тела, при его исполь­зовании уменьшается число основных уравнений и число членов в оставшихся уравнениях. Это обусловлено в основном тем, что принцип сохранения массы выражен в лагранжевых коорди­натах.

Мы уделили большое внимание различным системам коор­динат, с тем чтобы исследователи, приступающие к этой новой для них теме, имели представление об аналитических средствах, многие из которых не применялись к двигателю Стирлинга. Сле­дует ознакомиться со всеми указанными источниками, в част­ности с работами |20, 41, 45, 51, 55, 74]. Настоятельно реко­мендуем монографии [41, 51], а также превосходную работу Финкельштейна [74], в которой были заложены основы метода узлов.

В настоящее время газодинамический подход применяется Органом [45], который использовал решение, полученное ме тодом характеристик, непосредственно для расчета рабочих ха­рактеристик регенератора, применяя методы определения влия­ния сеток на нестационарное течение продуктов сгорания в ди­зельных системах, разработанные Бенсоном и Баруа [82]. Для применения к двигателям, работающим по циклу Стирлинга, этот метод, разумеется, требует введения некоторых модифика­ций, но они будут, видимо, не слишком сложными. Было уста­новлено [82], что коэффициенты потерь давления для сетки зависят от пористости, числа Рейнольдса, формы сетки и числа Маха (сжимаемости). Коэффициенты, справедливые для ста­ционарного течения, которые представлены в опубликованных работах и, следовательно, используются при разработке и кон­струировании двигателей Стирлинга, не зависят от числа Маха. Не вполне ясно, каково его влияние на данные для стационар­ного течения, используемые при расчете двигателя Стирлинга; согласно результатам Мартини [6], значения перепадов давле­ния, рассчитанные при использовании этих данных, в некоторых случаях приходится умножать на коэффициент 2,9, чтобы до­биться соответствия измеренным величинам. В работе Бенсона и Баруа [82] также предложен метод определения потерь дав­ления в нестационарном потоке, и поэтому читателям, намере­вающимся применить метод Органа, следует ознакомиться с этой работой.