Кривошипно-шатунный привод
Чтобы описать движение основного кривошипно-шатунного механизма привода, удобно использовать в качестве примера двигатель модификации альфа. Механизм с U-образным кривошипом двигателя Р-40 фирмы «Юнайтед Стирлинг», является,
|
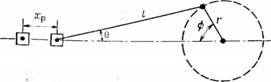
Рис. 2.35. Перемещение поршня кривошипно-шатунного приводного механизма. |
По существу, кривошипно-шатунной системой и, следовательно, может быть описан аналогичными соотношениями, за исключением того, что объем холодной полости будет меньше на величину объема поршня со штоком.
Из рассмотрения рис. 2.35, на котором представлена криво - шипно-шатунная система, находим, что объем, вытесняемый поршнем, равен произведению площади сечения поршня Ар на величину перемещения поршня х:
У(ф) = Арх, (2.72)
А из геометрических соображений получаем
Х = г (1 — cos ф) - J - / (1 — cos 6), (2.73)
НО г sin Ф = / sin 6, п = Llr, cos 6 = (1 — sin2 6)°-5. «Следовательно,
Л; = г {(1 - cos ф) + п [1 - (1 — sin2 ф/п2)0-5]},
V (ф) = гАр {(1 - cos ф) + п [1 - (1 - sin2 ф/пП.
Однако рабочий объем цилиндра равен 2гАр в таком случае V (ф) = {(1 - cos ф) + п [1 - (1 - sin[2] ф/п2)0-5]}. (2.74)
Это соотношение выражает изменение объема полости расширения, вызванное движением поршня, и аналогичное соотношение с использованием угла поворота кривошипа (ф — а) описывает изменение объема полости сжатия. Величина а — это фазовый угол по кривошипу. Если бы использовался приводной механизм поршня в полости сжатия, имеющий другие размеры, то соотношение не изменило бы своей функциональной формы, но значения г, I или Ар могли быть другими, хотя п как безразмерная величина могла остаться той же самой. При использовании модели синусоидального движения в соотношении остается лишь первый член, содержащий тригонометрическую функцию, а именно
У(ф)=^ (I-cos ф), (2.75)
Где ф = 0, когда поршень достигает верхней (или нижней) мертвой точки. Отклонение от синусоидального закона движения определяется членом nil—(1 — п~2 Sin2 ф)°>5]. При бесконечном возрастании п этот член стремится к нулю, и, следовательно, при больших значениях п предположение о синусоидальном законе движения обеспечивает достаточно высокую точность. Реальные значения п заключены в диапазоне 3,5—5. При этих значениях п можно легко оценить влияние высших гармоник, выражая изменение объема в виде ряда Фурье, как это делалось при анализе динамической балансировки приводного механизма:
/ sin20 sin[3] ф sinвФ
V (</>) = (1 — cos ф + А + В cos 2ф + С cos 4</> + D cos 6</> + ...),
(2.76)
__ з 5 fi__n,________ I_ ■ 15 N
Где л — 4п -+- 64/гз 196/г5 , Ts — ^ 4п -+■ 16tt3 + 392/г5 ) .
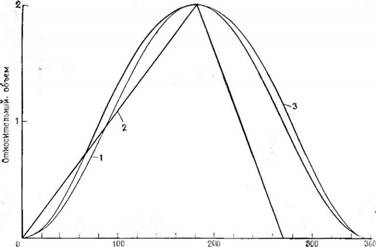
Таким образом, отличие действительного изменения объема ют изменения объема при синусоидальном движении практически точно выражается величиной 0,07(1 — cos 2Ф). На рис. 2.36 представлены изменения объема при прерывистом, синусоидальном и реальном (п = 3,5) движениях поршня. Очевидно, что движение кривошипно-шатунного механизма отличается от прерывистого, и характеристики этого основного привода вряд ли
|
Угол поворота кривошипа грай "Рис. 2.36. Сравнение изменений объема при идеальном, синусоидальном и реальном движениях поршня (кривошипно шатунный механизм.) !—движение по синусоидальному закону; 2- прерывистое движение; 3 — реальное движение. |
Можно сколько-нибудь существенно улучшить. При возрастании п изменение объема становится ближе к «синусоидальному», в то время как при уменьшении п возникают очевидные трудности. Учет второго гармонического члена позволяет точно рассчитать реальное изменение объема, однако даже учет лишь одной первой гармоники, т. е. использование предположения о синусоидальном движении, позволяет получить довольно точные данные, по крайней мере на начальных стадиях проектирования двигателя.