КОМБИНИРОВАННЫЙ АНАЛИЗ
В разработанных к настоящему времени методах комбинированного анализа рассматриваются лишь термодинамические, газодинамические и теплообменные вопросы нестационарного течения рабочего тела при его движении в системе двигателя. Вопросы, связанные с динамикой машины и сопротивлением материалов, не включаются в рассмотрение, п это может иметь в дальнейшем нежелательные последствия. Например, методы комбинированного или раздельного анализа, использованные при проектировании или оптимизации двигателя, могут дать результаты, не совместимые с требованиями, которые следуют из рассмотрения динамики машин или сопротивления материалов. Следовательно, методы комбинированного анализа (или анализа 3-го порядка) должны применяться только на последней стадии предварительной проработки или проектирования, как показано на рис. 3.1, когда все основные требования выполнены. В открытой литературе опубликовано несколько методов комбинированного анализа, которые имеют практически одинаковый аналитический подход и различаются лишь методами решения получающейся системы уравнений. В опубликованных работах, на наш взгляд, уделяется чрезмерное внимание выводу основных уравнений, и, хотя само по себе это и полезно, в зависимости от типа публикации зачастую может создаваться впечатление, что эти уравнения получены впервые и применимы исключительно для двигателя Стирлинга. И то и другое почти полностью неверно. Рабочий процесс в двигателе Стирлинга представляет собой нестационарное течение рабочего тела в каналах переменного сечения при наличии трения и теплообмена. Подобные течения были подробно рассмотрены, например, в известных работах [40—42]. Чтобы применить основные уравнения к двигателям Стирлинга, нужно задать граничные условия, отражающие особенности газодинамики в таком двигателе, н учесть течение сквозь металлические сетки; именно это и следует подчеркнуть.
Стандартным подходом к решению подобных газодинамических задач является метод характеристик [44]. Однако этот подход применяется лишь в работах [43, 45], в то время как остальные исследователи предпочитают так называемый метод узлов. Подробное описание и сравнение различных подходов выходят за рамки нашей книги, но мы сделаем некоторые замечания и опишем физические основы анализа. Будут указаны соответствующие источники, особенно те, в которых представлены программы численного расчета на ЭВМ. В готовящейся к печати работе [46] предполагается дать полное описание методов комбинированного анализа, которые пока не представлены в открытой литературе.
Решение любой газодинамической задачи должно удовлетворять уравнениям неразрывности, количества движения и энергии. В случае нестационарного течения уравнения получаются нелинейными, и пока не имеется общего метода их решения. Хотя с помощью быстродействующих счетных машин можно решить полную систему уравнений для трехмерного течения, в настоящее время для течений, встречающихся в двигателе Стнрлинга, в достаточной степени разработаны лишь методы расчета одномерного потока. Это ограничение означает, что все основные параметры считаются зависимыми только от одной пространственной переменной и времени. При использовании этого основного предположения подразумевается, что скорость потока параллельна единственной пространственной координате и что все поверхности, перпендикулярные этому направлению, являются поверхностями постоянной скорости и постоянных параметров состояния. Задача о нестационарном течении решена, если в любой момент времени в любой точке системы известны параметры состояния, определяемые двумя параметрами термодинамического состояния, и скорость потока [54]. В принципе можно определять любые три независимых параметра, но предпочтительнее те, которые можно измерить экспериментально, чтобы получить возможность подтвердить математическую модель.
Многими исследователями рассматривались такие явления нестационарной газодинамики, как возникновение пульсаций и возвратного течения, а также влияние плавного и резкого изменения площади проходного сечения, трения, подвода тепла, движения поршня, течения сквозь металлические сетки и т. п. Эти исследования не проводились специально для двигателя
Стирлинга, но совершенно очевидно, что в открытой литературе можно найти все необходимые методы исследования, и тем не менее, если не считать отдельных попыток, все это богатство теоретических знаний совершенно не использовалось. Теоретические исследования, методы решения и численного расчета можно найти в уже упоминавшихся работах [40—42], а также в публикациях [44, 45, 47—53]. Метод узлов имеет ту же теоретическую основу, но совершенно иную методику решения. Вопрос о применимости этой методики вызывает сомнения, но окончательный выбор нельзя сделать до тех пор, пока не будет
|
Dx
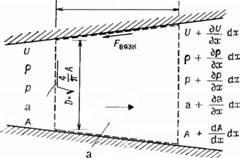
Рис. 3.5. Типичный контрольный объем. |
Разработан полностью обоснованный теоретический метод. Метод характеристик доказал свою состоятельность применительно ко многим задачам нестационарной газодинамики, но не к двигателю Стирлинга. Какой бы метод ни применялся, остаются проблемы определения корреляционных соотношений теплообмена и аэродинамического сопротивления, так что приходится по-прежнему применять те же самые уравнения «эквивалентного» стационарного течения, которые использовались в анализах более низкого порядка. Следовательно, в настоящее время методы комбинированного анализа лишь олицетворяют более строгий термодинамический и газодинамический подход и поэтому естественно задать вопрос: а есть ли смысл повышать на порядок сложность анализа и точность численного расчета, если остаются нерешенными многие фундаментальные проблемы математического моделирования явления? С точки зрения конструирования и оптимизации двигателя на этот вопрос следует дать отрицательный ответ, но для достижения более глубокого понимания механизмов, управляющих рабочими процессами в двигателе Стирлинга, и взаимосвязи между газодинамикой и теплообменом требуются более строгие подходы. Теория и способы решения с помощью метода характеристик описаны в указанных выше работах, а аналогичные сведения с использованием метода узлов представлены в работах [20, 39, 55. 56], где приводится и полное описание программ численного расчета. Рекомендуется также изучить работы [57, 58, 60].
Теперь представим основные уравнения и сделаем краткие замечания по поводу их решения. Уравнения выводятся согласно трактовке Шапиро 140]. При изложении решения методом характеристик мы следуем не Шапиро, который опирался на оригинальную работу [59], а методике, предложенной в работе [42].
Рассматривая типичный контрольный объем, показанный на рис. 3.5, можно вывести основные уравнения:
Уравнение неразрывности
Д (рUЛ) . д , . . ч
Dp , DU , т, Dp . U dA ,. Уравнение количества движения
Закон сохранения количества движения требует выполнения следующего соотношения
Силы давления+Вязкие силы (сопротивление) = = Изменение количества движения в контрольном объеме
По времени + Поток количества движения, (3.73)
Силы давления = —(РЛ) dx + р dx, (3.74а)
OLJ2
Вязкие силы = — f nD dx, (3.746)
Д
Изменение количества движения по времени = (pAUdx),
(3.74в)
Поток количества движения = (pAU2) dx. (3.74г)
После некоторых алгебраических преобразований уравнение (3.73) сводится к следующему:
На основании уравнения неразрывности член, стоящий в скобках, равен нулю. Итоговое уравнение количества движения
Удобно записать в следующем виде (замечая, что А = &D[4]/4): + + + = (3.76)
Г f U2 U 4 ,1 77Л
Отношение U/U введено для того, чтобы обеспечить правильный знак перед Gb, поскольку Gb действует в направлении, противоположном направлению течения. Уриелли [55] предложил использовать так называемый коэффициент трения Рейнольдса FR, определяемый формулой
FR = F Re, (3.78)
|
(3.78а) |
Р UD
Где Re =
Модуль числа Рейнольдса вводится по тем же соображениям, что и модуль скорости в соотношении (3.77).
Уравнение энергии
В соответствии с первым началом термодинамики Тепловой поток = Мощность на валу +
/Изменение внутреннейЧ + 1 энергии в контрольном 1 + ( торможения J> (3.79) V объеме по времени / г
Т- Е. Q = Ws + d(E)cv/di + dHBP, (3.80)
Где Q = qpA dx, (3.80а)
Д (E)cv/dt = d/dt [рA dx (CVT + -£)], (3.806)
ДНЕР = д/дх [рUА (СуТ + + Р/Р)] Dx, (3.80в)
— 0 для контрольного объема (но см. разд. 3.5.3) (3.80г)
После довольно сложных выкладок и использования соотношений. которыми выражаются
1) субстанциональная производная
Уравнение (3.79) можно записать в виде
А2. / 1 Dp Dp
Q =-------- 2—1-9 —------------------- Ч - '3.84)
P(V - 1) a2e Dt Dt J
Это «определяющее» уравнение системы. Его форма будет иной
Для
1) других уравнений состояния;
2) многокомпонентных рабочих тел;
3) рабочих тел, в которых проходят химические реакции.
Течение смеси газа с частицами, содержащей взвешенную конденсированную фазу, рассмотрено в гл. 14 работы £41J. Уравнения для газа с химическими реакциями были полностью выведены в работе Ридера [53], где показано, что определяющее уравнение имеет те же самые члены, но «равновесное» значение скорости звука заменено «замороженным».
Для облегчения решения и удобства представления расчетных результатов все параметры, входящие в уравнение, нормализованы, т. е. приведены к безразмерной форме. Способ нормализации зависит от выбранного метода решения, класса счетной машины и желания исследователя.