Идеальный двигатель Стирлинга
В идеальном двигателе Стирлинга тепловая энергия, выделяемая в процессе 4—1, должна быть возвращена рабочему телу в процессе 2—3, и это осуществляется с помощью регенератора, который представляет собой, по существу, насадку из проволочных сеток, которая попеременно выделяет и поглощает тепловую энергию. Она действует как «тепловая губка». Как отмечалось выше, регенератор расположен между нагревателем и холодильником. Теперь следует ■учесть эффективность регенератора. Если рабочий процесс регенератора неидеальный, процесс 2—3 в регенераторе не завершается полностью и газ достигает лишь состояния 2' (рис. 2.1), процесс 2'—3 может происходить в результате теплообмена с окружающей средой. Эффективность регенератора е можно выразить формулой
Е = (Г2'-7)/(Г3-7), (2.3)
И, следовательно, при определении КПД идеального двигателя нужно учесть тепловую энергию Q2rз. затраченную на теплообмен с внешней средой. Теперь можно найти выражение для термического КПД идеального двигателя (но не идеального считать необходимые параметры следующим образом:
Лтгрм = Wx/Qs, (2.4)
Тде Wx — полезная работа. Рассматривая рис. 2.1, можно рассчитать необходимые параметры следующим образом:
|
|
|
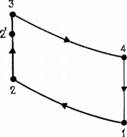
Рис. 2.1. Диаграмма идеального двигателя. |
|
V Состояния |
4 2
= R34+ Г12 = 5 Pdv + pdv^
= mRT3 J dV/V + mRTt J dV/V = mRT3 In rv — mR Г, In rv. (2.5)
Если теперь ввести отношение температур
1 = 777-3.
То соотношение (2.5) можно переписать в виде
Wx = mCvT3(-)(-%)nrv, (2.6)
Где остальные обозначения имеют общепринятый смысл. Теперь нужно определить тепловую энергию, подводимую к двигателю. В общем случае тепловая энергия подводится извне в процессе 2' — 3 — 4, так что
Qs = <?2'з + <Эз4- (2.7)
Первое слагаемое выражает тепловую энергию, подведенную в ходе изохорного процесса, которая определяется формулой
Q/я = niCv (?'з - Т2<),
А второе выражает тепловую энергию, подведенную в ходе изотермического процесса:
Q3I = MRT3 In Rv, Так что соотношение (2.7) принимает вид
Qs = mCv (7*3 - 7» + mRT3 In rv. (2.8)
Чтобы выразить все параметры через максимальную и минимальную температуры (Т3 и Т соответственно), используем параметр е, такой, что
Т2' = Т3 [е + (1 — Е)|],
И тогда
Qs = MCvT3 [(1 - е) (1 - I) + (у - 1) In rv]. (2.9)
Следовательно, термический КПД г|терм двигателя можно найти, разделив соотношение (2.6) на соотношение (2.9); тогда
"Птерм = (V - 1) (1 - 8) In Гу/Н 1 - (1 - в) + (Y - 1) In Гу]. (2.10)
Если эффективность регенератора равна 100%, т. е. е = 1, то соотношение (2.10) сводится к формуле (2.2), выражающей КГ1Д идеального цикла Стирлинга (и цикла Карно). Отношение КПД идеального двигателя Стирлинга к КПД идеального цикла Стирлинга равно
Ri« = (v-l)lnrv/[(l-8)(l-|)-(Y-l)lnrK]. (2.11)
Кроме того, можно определить безразмерный параметр полезной работы идеального двигателя W0:
.у. ___ ИнДикаторное среднее эффективное давление ________ /о 1 91
W0 — ■ — — 1Z.1ZJ
= (1 - l)rvlnrv/[Urv- 1)]. (2.13)
|
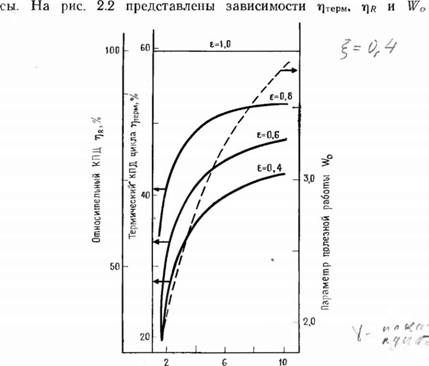
Этот параметр полезной работы служит в некоторой степени мерой удельной мощности двигателя Стирлинга, и с его помощью можно оценить размеры и режимы работы (через давление и скорость) двигателя. Ниже мы рассмотрим эти вопро-
Сглепен'ь сжатия г^ Рис. 2.2. Параметры идеального цикла в зависимости от степени сжатия. |
От е и rv при отношении температур | = 0,4. Приведенные данные не являются произвольными, они типичны для реального двигателя.