Доклады о будущих и современных технологиях
ЗАДАЧА ОПТИМАЛЬНОГО ПРОЕКТИРОВАНИЯ БРУСА ПРЯМОУГОЛЬНОГО СЕЧЕНИЯ
Н. А. Виноградова, Ю. Д. Таршис
Научный руководитель - Ю. Д. Таршис, д-р техн. наук, профессор Ярославский государственный технический университет
Данный вопрос можно рассматривать как установившеюся связь между рациональным подходом древних строителей и возможностями оптимального проектирования. В строительной практике приходилось вытесывать прямоугольные балки из круглых бревен, при этом ширина и высота балки могли быть сделаны производно.
 Среди прямоугольных сечений, которые можно вписать в контур бревна, существует такое, для которого величина сопротивляемости изгибу (то есть момент сопротивления) будет наибольшей. Эта задача известна как задача Парана (1666-1716), французского математика, внесшего большой вклад в теории изгиба балки. Решение дается в следующей форме.
Среди прямоугольных сечений, которые можно вписать в контур бревна, существует такое, для которого величина сопротивляемости изгибу (то есть момент сопротивления) будет наибольшей. Эта задача известна как задача Парана (1666-1716), французского математика, внесшего большой вклад в теории изгиба балки. Решение дается в следующей форме.
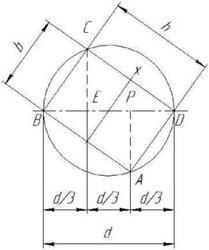
Следует разделить диаметр на три части и восстановить перпендикуляры ЕС и АР, образовавшийся прямоугольник АВСБ представляет собой искомое сечение балки, в котором АВ = Н - высота, АБ = Ь - ширина. Тогда на основании известного соотношения для прямоугольного треугольника ВС2=ВБВЕ получаем, что Ь=с1/л[3.
Решим эту задачу с использованием дифференциального исчисления, т. е. как оптимальную:
. '2-Ъ2
Момент сопротивления вписанного прямоугольника относительно оси будет равен:
И/ = 6 = 6
Для отыскания максимума возьмем первую производную и приравняем ее к нулю:
Откуда Ь=<1/!3.
Получился тот же результат.