Доклады о будущих и современных технологиях

Продольно-поперечный изгиб гибких стержней

А. Е. Кюккер, М. В. Колганова, Н. В. Бадаева

Научный руководитель - Н. В. Бадаева, канд. техн. наук, доцент Ярославский государственный технический университет

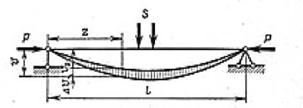
Изгиб, вызываемый одновременным действием продольных (направ­ленных по оси), сжимающих и поперечных сил, называется продольно­поперечным.

Расчет гибких стержней, которые работают на сжатие с изгибом, не­обходимо выполнять с учетом возникающих деформаций, по так называе­мой деформированной схеме. Вследствие деформации стержня возникают перемещения, поэтому продольная сжимающая сила создает дополнитель­ные изгибающие моменты, пренебречь которыми нельзя.

Так как задача продольно-поперечного изгиба является статически не­определимой для её решения необходимо составить и решить дифферен­циальное уравнение оси изогнутого бруса.

С12 V и Р _ М0

С1г2 е;У Е

Где М0 - момент только от поперечных сил

Точное решение требует больших преобразований и сложных выво­дов, особенно если балка делится на несколько участков, для которых при­дется писать свои уравнения и проводить их интегрирование. Для упроще­ния задачи применяют приближенный способ определения прогибов при продольно-поперечном изгибе. Нагрузку можно представить в виде суммы двух прогибов: V = и0 4- Аи,

Где 17& - прогиб, вызываемый действием только поперечной нагрузки без учета силы Р;

Л;' - дополнительный прогиб, от действия сжимающей силы Р.

После череды преобразований:

-I, - щ

1 —:—?~,

Где РКр =

/ - момент инерции, соответствующий изгибу в данной плоскости,

0<Р< 0,8Ркр.

Следует иметь в виду, что в инженерных задачах, которые встречают­ся в строительной практике, сжимающая сила не превышает 0,5- 0,6Ркр, по­этому приведенная выше формула будет вполне достаточной для практи­ческих целей.