Доклады о будущих и современных технологиях
БАРИОПЕРАЦИОННЫЙ МЕТОД РЕШЕНИЯ СДУ 4-ГО ПОРЯДКА
С. В. Антонов, А. В. Бородин
Научный руководитель - А. В. Бородин, канд. физ.-мат. наук, доцент Ярославский государственный технический университет
Следуя работе «Одномерный барилинейный анализ и изоспектраль - ные уравнения Шредингера» (Бородин А. В., Ярославль: ЯГТУ, 1997 г.), рассматривается сначала система барилинейных АУ вида:
|
(1) |
![]() (< а >1+< а >12< Х >2=< Ь >li
(< а >1+< а >12< Х >2=< Ь >li
1< а >2 і < X >!+< а >22<х >2=< Ь >2-
Затем для неё решается задача на собственные значения и собственные векторы:
|
< а > < а > |
|
'<%> X X > |
|
12 22у |
|
||
|
||
Полученные решения используем для решения системы барилинейных дифференциальных уравнений:
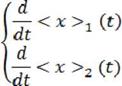
|
=< a >ь<х >1 |
![]()
|
=< a >2i< х >± |
![]()
|
(3) |
![]() +< а >12< х >2
+< а >12< х >2
+< а >22 < х >2
Которая на языке обычного нам анализа, является нелинейной системой, типа Абеля. Для начала рассматривается «сокращённая» систему барилинейных дифференциальных уравнений с постоянными коэффициентами:
|
=< а >12 < х >2 |
![]()
|
=< а >22 < х >2 |
![]()
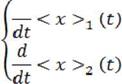 <1
<1
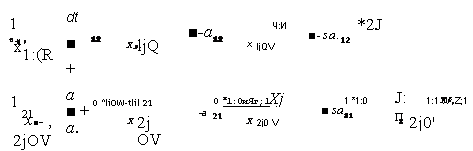
Которая равносильна нелинейной системе ДУ вида:
|
-X |
|
І, dt |
|
Dt ■ + а |
|
*2joI |
|
Ч:И |
|
1 12 - V і' X1:(R |
|
■-а |
|
■-sa. |
|
12 |
|
12 |
|
12 |
|
ХЛ. |
|
X |
|
LjQV |
|
LjQV |
|
J:п |
|
О ж1:0иЯг;1 |
|
Xj |
|
1 *1:0 1:1 W* Z;1 |
|
X-, |
|
0 ^liOW-tlil 21 |
|
1 21 - , 2jOV |
|
■ + a. |
|
-a |
|
■ sa |
|
21 |
|
21 |
|
X■ |
|
X |
|
X |
|
X |
|
2jOV |
|
2j0 V |
|
2j0' |
 |
|
|
|
|
|
Решая линейную систему ДУ (3'), получим общее решение системы
ДУ (4).