COMPUTATIONAL WELDING MECHANICS

Evolution of Microstructure Depending on Temperature

4.1 Introduction and Synopsis

One of the most widely used methods for joining metal in engineering is fusion welding. The progress made in the chemical and oil industry, aerospace, shipbuilding, structures, etc. heavily relies on reliable welds. Potential losses and risk to human life involved in weld failure have resulted in stringent material and welding process control requirements.

The energy input causes a thermal cycle that drives the grain growth and microstructural changes in the heat affected zone. The HAZ ranges from the solid-liquid transition zone on its inner surface to the unaffected base metal on its outer surface. A large austenite grain size in steel welds along with transformation products such as martensite and bainite renders the base metal susceptible to brittle fracture. In addition these hard and brittle products can make the weld sensitive to stress and corrosion and can also lead to the formation of stress induced cold cracks and pose most danger in practice.

Microstructure computations are also fundamental to predicting the behavior of the HAZ, The HAZ is the most sensitive area of the weld joint and in steel the mechanical properties of the joint depend on austenite grain size and transformation products.

At a macroscopic level, the metal physics can be described by scalar fields specifying the fraction of each phase present, the composition of each phase and the grain size of each phase at each spatial point in the heat affected zone. In low alloy steels, the phases of greatest interest are ferrite, pearlite, austenite, upper and lower bainite, martensite, carbide and liquid. Most steels used in welded structures are produced with a ferrite-pearlite microstructure or a ferrite and austenite-martensite constituent. When these steels are heated above AeX or the eutectoid temperature, the pearlite or austenite-martensite constituent rapidly transforms to austenite with the same composition. Even though the heating rates are high, superheating only amounts to a few tens of degrees; approximately 80°С is common. So in most cases the assumption that the transformation occurs at equilibrium can be tolerated. However, the homogenization of this carbon austenite region is much slower. It is a function of the temperature, time and the distance between high carbon regions.

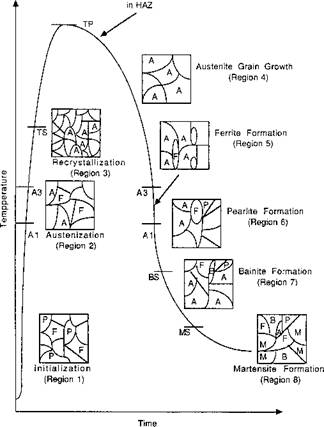
The various regions into which the thermal cycle can be divided are shown in Figure 4-1.

A group of researchers [11, 12, 13 and 14] have attempted to predict the hardness distribution in the HAZ without taking into account the phases present in the microstructure. Another approach to the HAZ microstructure prediction has been proposed by Ashby, Ion and Esterling [6, 9 and 10].

The weld thermal cycle is predicted by using a modified version of Rosenthal’s [15] analytical equation. One drawback of this model is the weakness of the Rosenthal equation, which ignores the distribution of power density and assumes that thermal conductivity and specific heat of the material are independent of temperature.

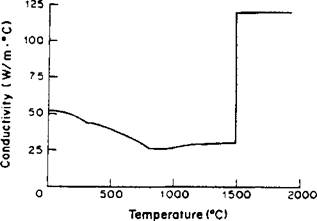
The thermal conductivity varies as shown in Figure 4-2. Here the conductivity in the liquid has been set at a relatively high value in an attempt to take into account the convective stirring at the high velocities (~ 1 m/s) found in weld pools [32].

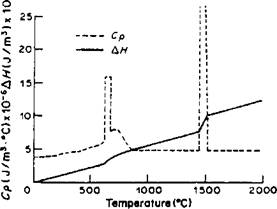
The heat capacity and the latent heats vary also as shown in Figure 4-3.

A third set of workers have modified Kirkaldy’s hardenability algorithm [16, 17, 18 and 19] to predict the microstructure of the HAZ. This algorithm can be used to isolate the individual effects of weld process parameters. It also highlights the effect of austenite grain growth on the HAZ microstructure. For example, CCT diagrams and Jominy-end-quench hardness curves can be generated from the Kirkaldy system for most low alloy steels. The austenite decomposition relationships in this scheme are formulated as ordinary differential equations ODE (see the general form in equation 4-21 and the special form for the austenite transformation to ferrite in equation 2-19) which must be integrated numerically to compute the fraction of each microstructural component formed. This can be CPU intensive if a simple Euler integration scheme is used.

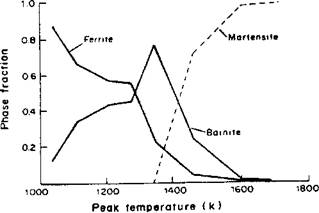
An adaptive integration scheme has been suggested to increase computational efficiency [22]. A computed microstructure distribution across a small bead-on-plate weld is shown in Figure 4­4 to demonstrate the sensitivity of the system. Similar computations that are transient are possible because the microstructure is tracked over the entire thermal cycle.

This group of researchers, [20, 21 and 22], have shown that the hardenability algorithm proposed by Kirkaldy can predict the resultant microstructure of the HAZ quite accurately. The main draw back in their computation is the use of inefficient integration techniques to solve the austensite decomposition relationships. This problem limited accuracy and made their algorithm CPU intensive and costly.

Although many factors can affect the micro structure of a metal, the thermal cycle is the dominant factor in welding processes. It is the peak temperatures and the heating and cooling rates in the thermal cycle that control the phase changes and microstructures. When the thermal cycle reaches its steady state, the microstructural evolution will, in most cases, also reach a steady state.