COMPUTATIONAL WELDING MECHANICS
Evolution of Microstructure Depending on Deformations
The thermal cycle imposed on any welded object causes thermal expansions and contractions to occur that vary with time and location. Since this expansion is not uniform, stresses that appear in hot regions near the weld are restrained by cooler regions further away. Plastic deformation, occurring as a result of these stresses, leads to residual stresses in the object that remain after the temperatures have returned to ambient levels. Thus, the use of welding in the fabrication or repair of pressure vessels introduces residual stresses in the weld itself and in the base metal. An accurate knowledge of the magnitude and distribution of the residual stresses is useful when assessing the fitness of the vessel.
Three fundamental dimensional changes of a flat welded plate are:
- transverse shrinkage;
- longitudinal shrinkage;
- angular distortion (rotation around the weld line)
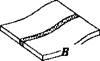
From a more detailed point of view, the welding deformations can be classified as [48], Figure 5-1:
- transverse shrinkage - shrinkage perpendicular to the weld centerline;
longitudinal shrinkage - shrinkage in the direction of the weld line;
angular distortion-distortion caused by nonuniform temperature distribution in the through-thickness direction; rotational distortion-angular distortion in the plane of the plate due to thermal expansion or contraction; bending distortion-distortion in a plane through the weld line and perpendicular to the plate;
buckling-distortion caused by compressive stresses inducing instability particularly when the plates are thin
|
uckling |
|
Longitudinal shrinkage |
|
|
|
Al |
Bending
distortion
|
Rotatinal distortion |
Transverse shrinkage
Angular shrinkage
Figure 5-1: Various types of welding distortion, from [48].
Material modeling is, together with the uncertainty in the net heat input, one of the major problems in welding simulation [1 and 2]. The thermal analysis is, more straightforward than the mechanical analysis. It entails few numerical problems, with the exception of the large latent heat during the solid-liquid transition, and it is easier to obtain accurate values of the thermal properties rather than the mechanical properties of a solid.
McDill et al [3] investigated the relative importance of the thermal and mechanical properties of stainless and carbon steels in welding simulations. Two bars of dimension 20in x 2in x 0.5in were “welded” along the free edge. No fixture was used. One bar was made of stainless steel and the other of carbon steel. The resultant
radius of curvature was compared with the computed values for the material properties of carbon steel (MS) or stainless steel (SS). The results are shown in Table 5-1. The somewhat unexpected conclusion was that the thermal properties play a more important role than the mechanical properties in explaining the different behavior between these steels. This is due to the fact that the thermal dilatation is the driving force in the deformation and the bar is free to bend. The thermal dilatation is determined by the temperature field and is, therefore, strongly influenced by the thermal properties. In other words, the thermal dilatation together with the temperature distribution is important for the deformation [1].
|
Table 5-1: Curvature for combinations of thermal and mechanical properties [3]. MS mild steel, SS 304 stainless steel
|
|
The complete thermo-mechanical history of a material will influence its material properties. However, in many cases an adequate approximation is to make properties a function only of the current temperature and effective plastic strain. |
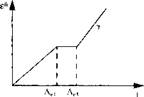
The simplest and most common approach is to ignore the microstructure change and assume that the material properties depend only on temperature. Then, for example, one might assume that the thermal dilatation is the same during heating and cooling, as in Figure 5-2a.
|
|
|
Dependency on current temperature only. |
|
|
|
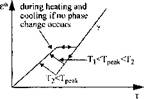
Dependency on current temperature and peak temperature. b) |
|
|
|
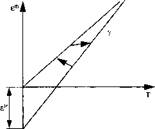
Model of properties of different phases which must be combined with a model for microstructure evolution. |
|
Figure 5-2: Different methods for modeling dependency of thermal dilatation on phase changes in ferritic steel, from Lindgren [1]. |
Distortion and residual stress in welds are caused by nonlinear material behavior. For sufficiently low stresses and sufficiently short times, the stress strain relationship for solids is linear elastic. For sufficiently high stresses and sufficiently long times, the stress strain relationship is nonlinear. What a sufficiently low stress and a short time is, depends the problem, its material type, its microstructure and the temperature.
For Newtonian fluids the stress strain rate relationship is linear. The nonlinear behavior of a solid tends to be strain rate dependent at high temperatures and sufficiently long times. This means that the
stress is a function of the strain rate. The plastic deformation is often associated with the thermally activated motion of dislocations in the presence of a deviatoric stress field. This is called rate dependent plasticity. At low temperatures, the strain rate is a nonlinear function of stress rate and is not a function of stress.
|
0,4 0,6 rel. Temperatur, TITS |
|
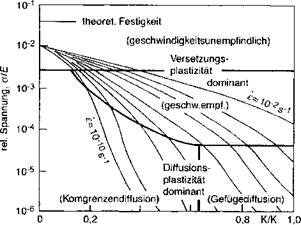
Figure 5-3: Sketch of an Ashby diagram illustrating deformation mechanisms and different strain rates. Different deformation mechanisms in different temperature and stress regimes are shown, from [43 and 44]. |
|
|
|
■jT'-^Versetzung |
|
Diffusion |
|
a--------- stationar |
|
|
Plastizitats- mechanismen
To accurately predict stress, residual stress and distortion in welded structures, one must know how the material responds to a given stress or strain, i. e., which constitutive equation to use for a given state of the material and loading condition. One must know which constitutive equation is most appropriate as well as the material properties that describe this behavior such as yield stress or deformation resistance. The best known representation of material behavior versus strain rate and temperature are Ashby diagrams, Figure 5-3.
The mechanisms for the plastic deformation vary due to the large temperature range involved. In welds, the strain rate is usually less than 0.01 /second. A crack driven by elastic unloading could have much higher strain rates but that is not considered here. The Ashby diagram has several striking features. First there are many different mechanisms for deformation. Therefore one should not expect a
simple function. Second the flow stress rises rapidly with decreasing temperature. Third the difference in flow stress for strain rates of say 0.0001/s and 0.01/s narrows rapidly as temperature is decreased.
The homologous temperature is defined as the current temperature in Kelvin divided by the melting temperature in Kelvin. The authors recommend that a linear viscous model be used at a homologous temperature above 0.8. Rate dependent plasticity be used down to a homologous temperature of 0.5 and rate independent (usually with von Mises plasticity), [51], for lower temperatures.