COMPUTATIONAL WELDING MECHANICS
Deformation
By introducing a reference configuration in the deformation equations, any configuration in the deformation process can be expressed in that reference configuration. Figure 5-8 shows the displacement of a particle from its initial position '“'x to the current position 'x. The particle's reference position can be related to both deformed positions through a motion:
x = x(rx, t) (5-23)
|
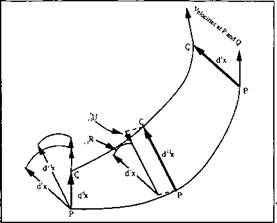
Figure 5-8: Displacement, stretch and rotation of a vector d' 'x at position i-1 to d’x at a new position i. Both have unique mappings to the reference configuration, from [6]. |
The deformation gradient tensor is the simplest to define in terms of the deformation equations. This tensor also includes more information than the strain tensor. R and U can be obtained by a polar decomposition of a relative deformation gradient tensor [6, 21,
22 and 23]. A polar decomposition F=R U describes both the rotation R and stretching U experienced during the deformation.
The deformation gradient 'Fmaps vectors dxr to vectors d'x. Hence, in this context ‘F is defined as the tensor whose rectangular Cartesian components are the partial derivatives d'xk/dr;tm. The
tensor 'F operates on an arbitrary infinitesimal material vector d' x at 'x. It associates the vectors d'x and d’x as:
d'x-'F - d'x (5-24)
d‘xk=^r^d"xm (5-25)
d Xm
One advantage of the Lagrangian formulation is that it traces the history of changes of mechanical properties in the deformed material naturally. In the updated Lagrangian formulation the mechanical properties are updated in every time step. At the beginning of every step, all history results are treated as initial conditions. The formulation deals with the same material points in the final and initial configurations. Without deformation, a local coordinate system will remain unchanged in two configurations. An infinitesimal vector is computed in the local coordinate system.
When the deformation occurs between two configurations, the local coordinate system can change its length and direction. So does the infinitesimal vector. In general, this local coordinate system differs from one point to another in a curvilinear coordinate system. Each element would no longer contain the same set of material points. The stress or strain history of deformation at a material point can only be found from an upstream position of a flow line. The position is currently taken by another material point and the local coordinate system at that position is unlikely to be the same one as that of the current point, even without deformation. A mapping strategy is necessary.
|
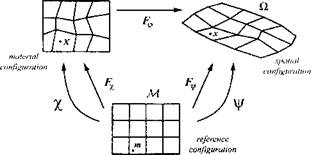
Figure 5-9: The AEL kinematics. The physical motion (pR of the solid or fluid is decomposed in the material motion % —~lR and the mesh motion j/ —R for a reference mesh M, adopted from [36]. |
Figure 5-9 indicates the relationships between the two deformed configurations and the undeformed configuration (reference configuration). By choosing a reference configuration and by mapping material points in any of the other configurations to the reference configuration, it is possible to obtain the deformation gradient tensor between any two deformed configurations. A few iterations are required to reach this indirectly from the deformed configurations to the reference configuration or in reverse order.
A relative deformation gradient tensor, M'F, between initial configuration і - 1 and final configuration i, can be defined:
Э' їх
In indicial form:
|
(5-27) |
ip =d'xmdrxk
drxkd'~lxn
Strain Increment Measurement
The stress in the current deformed configuration is called the Cauchy stress. If the current deformed configuration is mapped to
any other configuration such as a reference configuration in AEL (arbitrary Eulerian Lagrangian) or the configuration at the beginning of a time step, the Cauchy stress must be mapped to this configuration. Different mapping methods result in different stress types. The 2nd Piola-Kirchhoff, see chapter VI, and 1st Piola - Kirchhoff are examples. Each stress has its conjugate strain type defined such that the product o:s equals the strain energy density. For each stress-strain type, the constitutive equation must be defined. In the following, when the stress rate is specified, the corresponding strain rate is implied.
For a weld, in some local area within the heat affected zone, the displacement-gradient components can be of the order of unity. Thus, regions far from the heat affected zone may have large displacements and large rigid body rotations but small strains. Looking at a weldment, a large rigid body rotation from the original shape can often be seen with the naked eye. Infinitesimal strain measures can cause large errors in the residual stress analysis for welds. In such situations, finite strain measures should be used for weld analyses.
Many research papers have exploited various stress rates. The advantages and disadvantages of different stress rate formulations are described in references [18, 19, 20 and 21].
Along a flow line, the incremental logarithmic strain at point “i”
is:
Ae=i__;Rn(l_‘[U),;RT (5-28)
where M'7? is a rotation tensor rotating the stress or strain in the orientation of point “z-7” to that of the point “z”, and M't/ is a stretch
tensor describing the stretch from “/-7” to “i” in the orientation of stress (or strain) at “г-7”.
With Equations (5-21), (5-22), (5-26) and (5-27) a summary of the current formulation to calculate incremental stress from point “z - 7” to “z” along a flow line is as follows, from Gu et al [6]:
Step 1: Decompose the relative deformation gradient at point “z”,
(5-29)
Step 2: Calculate the incremental logarithmic strains at the strain orientation of point “i-1”,
Af' = ln (,._/[/)
. tr(Ae)
(5-30)
Ае = Ає'-Аєт
where Ae is the increment in the deviatoric strain tensor from i-1 to
i.
Step 3: Calculate the total Cauchy stresses at the stress orientation of point “i-1”,
' 1 ct + jDde
M
'o = ——Clee +Ae - Аєр - Аєс - АєТгр)
l+'v (5-31)
' P 14_'_l і/ ' 77
= — r—-МГ + — (Ae - Аєр-Аєс - AeTrp)
l+'v ]E l+'v
|
/І „ I „th i„Trp °m -£ ~ £ ) |
‘E 1-2'V
Step 4: Rotate the Cauchy stresses to the current orientation; and finally a translation to point i.
la=i_lR,-l(it7),i_lRT (5-32)
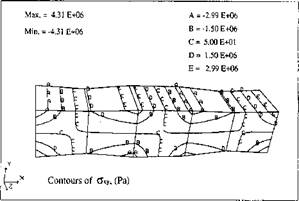
The current formulation has been tested in several ways. Thermal expansion and contraction were tested within the elastic range. The mesh size was 15.8 x 3.2 x 3 mm, divided evenly along the x - direction into 5 elements. Some results are shown in Figure 5-10.
The mid-element, element 3, had a temperature increment of 30°C. Although either a Lagrangian formulation or a steady state formulation reaches the same results in this case, the results have a different meaning. All elements but element 3 were kept at constant room temperature in the Lagrangian formulation. While a thermal
expansion occurred in element 3, there was no thermal expansion or shrinkage in any other elements. In the steady state formulation, the material in element 4 and element 5 had experienced a complete thermal cycle, heated up to 50°C and then cooled down to 20°C. A corresponding cycle of expansion and contraction occurred in these two elements. This example tested the elastic recovery of the model.
|
Max. = 5.00 E+06 A = -4.85 E+06 Min. = -6.63 E+06 B = -2’83 E+06 С = -8.16 E+05 D = 1.20 E+06 E = 3.21 E+06
|
|
Figure 5-10: Thermal expansion of a middle element in a 5 element bar. The two ends are fixed in x direction. The deformation scale factor is 50. |
A full scale computation was performed to analyze an edge weld on a thin flat bar. This example had been analyzed with the Lagrangian formulation [27]. The mesh in Figure 5-11 is created on a piece of material cut from the long strip, which contained a steady state temperature field. The mesh size is 543 x 50.8 x 6.35 mm.
In the transient analysis, this temperature distribution is shown at 100.5 seconds after welding started. With medium resolution in space and time, 65 steps in the Lagrangian formulation were required to reach this state for temperatures and stresses.
The material used is low carbon steel. The temperature dependent mechanical and thermal properties of AISI1020 are used. Weld speed is set at 5 mm/s. The heat source is a prescribed temperature field in a weld pool with a double ellipsoid shape. The source had length 8 mm, width 5 mm, and depth 3 mm. The resulting computed power input is 0.32 KJ/mm. The heat efficiency is estimated to be 70 percent.
|
Figure 5-11: FEM mesh designed for simulating the edge weld in the steady state, from [6 and 25]. |
|
Figure 5-12 shows the temperature field on the top and bottom faces of the plate.
|
Figure 5-12: Contours of temperature °С around the weld pool area. Top: symmetry plane; Bottom: outer surface.
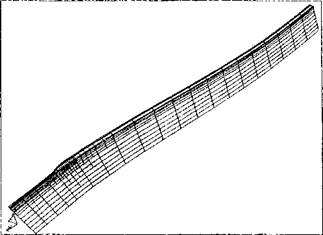
As often seen in a welding shop, thermal distortion bends the bar into the "S" shape seen in Figure 5-13. The displacements in this Figure have been magnified 30 times. In a welded structure, the residual stresses are highly localized, as is the element distortion around the weld path. Elements far from the weld path deform largely by rigid body rotations.
|
Figure 5-13: Distortion of the mesh after an edge weld. All displacements are enlarged 30 times. The undeformed mesh before welding is shown in grey lines. |
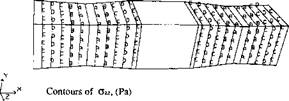
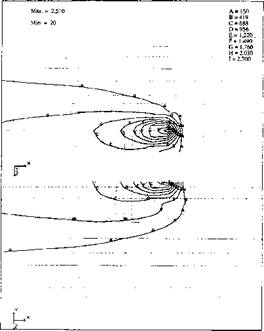
A detailed picture of the <JXX stress around the weld pool is given in Figure 5-14. For this weld the longitudinal stress &ix is the most significant one, with an average value 3 times larger than the other five stress components. It is the longitudinal stress that caused most of the distortion shown in Figure 5-14.
|
Figure 5-14: Contours of stress, <Jl:r (MPa), round the weld pool area. The phase transformation causes negative stress inside D after the weld pool. |
|
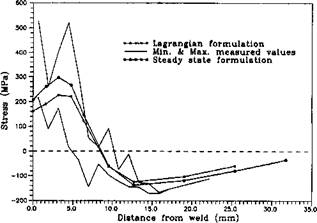
Figure 5-15 shows the computed values of the through-thickness average longitudinal stresses, comparing to the measured stresses and the stresses computed in the Lagrangian formulation. The measured stresses and the stresses computed in the Lagrangian formulation were provided by Oddy et al. [27].
|
Figure 5-15: Through-thickness average of longitudinal stress (Jxv versus distance
from welded edge. For the Lagrangian formulation [15], sampling data is from the mid-length of the weld path. For the current formulation, the data is from the near end of the path.
The computational results fit in the range of the measured data quite well. The steady state formulation has the better results near and far away from the weld center line. This difference is actually a problem of computational costs. In order to reduce computer time, the convergence tolerance was set too large in the analysis of reference [27] .With a more powerful computer and a smaller convergence tolerance, a more recent analysis in the Lagranian formulation, performed by Oddy et al [27], has shown similar results to those obtained in this steady state analysis.
The cost of computing the steady state solution is approximately the same as the cost of one transient Lagrangian step. If we use the Lagrangian method to compute the starting and stopping transient, but use the Eulerian method to compute the steady state part of the weld, the Eulerian method is more than 2000 times cheaper for the steady state portion of the 10 m weld. It is more than 2000 times cheaper because it need not remesh for each time step. Further more the mesh can be designed for the weld pool shape. More important, filler metal can be added naturally in this formulation. Figures 5-13 and 5-16 show the results of this analysis.
|
Figure 5-16: Steady state analysis of a butt weld with filler metal addition. The undeformed mesh is shown in faint dotted lines. The transient temperature for this analysis was shown in Figure 3-21. |
In most thermal analyses of welds performed to date, the mesh is not fine enough to resolve the rapid rise in temperature in front of the weld pool. The effect is that the computed strain rate can be much less than the real strain rate. Consequently the computed stress can be much less than the real stress.
When the convergence rate is described by the number of iterations of a nonlinear solver at a fixed tolerance, the test cases demonstrated that the convergence rate of the steady state formulation was the same as the convergence rate of the Lagrangian formulation for one time step. With this convergence rate the cost of
a steady state analysis is the same as the cost of one time step in the transient analysis.