ЧТО МОЖЕТ ВИБРАЦИЯ?

Закономерности и парадоксы самосинхронизации дебалансных внбровозбудйтелей

Перечислим в заключение основпые примечательные закономерности и парадоксы, характерные для само­синхронизации неуравновешенных роторов и представ­ляющие интерес для приложений.

1. Тенденция дебалансных вибровозбудителей к синх­ронизации; вибраііионное поддержание вращения. Деба - лаиспьте впбровозбудптелп с достаточно близкими поло­жительными парциальными скоростями со„ установлен­ные в некоторой механической колебательной системе с малой диссипацией, обнаруживают тенденцию к синхро­низации. Если валы дебалансных возбудителей, приводи­мых от двигателей асинхронного типа, будучи установ­ленными на неподвижном основании, вращаются с близ­кими угловыми скоростями Ы.1, то такие возбудители будут непременно самосннхроннзироваться при установке в указанной системе колеблющихся тел.

Вместе с тем при определеппых условиях самосинх­ронизация возможна и при сильной диссипации энергии в колебательной системе, а также при резко различаю­щихся о), и даже при некоторых со, = 0 или со, < 0. Пер­вый случай отвечает выключенным из сети двигателям соответствующих возбудителей (эффект вибрационного поддержания вращения), а второй — работе указанных двигателей в генераторном режиме, когда эти двигатели оказываются втянутыми во вращение, направление ко­торого противоположно направлению их вращения на неподвижном основании.

2. Эффект усреднения парциальных скоростей. Угло­вая скорость синхронного вращения вибровозбудителой со в условиях, указанных в п, 1, не больше, чем наиболь­шая, и но меньше, чем наименьшая из парциальных угловых скоростей со,.

3. Эффект передачи больших мощностей. Выравнива­ние угловых скоростей вращения роторов, обладающих различными парциальными угловыми скоростями со,, т. е, самосинхронизацию, можно трактовать как проявление вибрационной связи между роторами, т, е. передачи вра­щающих моментов или мощностей через колебательную систему от «более быстрых» возбудителей к «более мед­ленным». Для практических приложений явления само­синхронизации и эффекта вибрационного поддержания вращения первостепенное значение имеет тот факт, что указанные мощпости могут быть реально достаточно ве­лики: они имеют порядок произведения амплитуды вы­нуждающей силы F = тесог, развиваемой ротором, на так называемую эффективную амплитуду колебаний его оси Л* и на угловую скорость со (см. (12.26)). В частности, при F = 10е Н, А * = 0,25 • 10-г м и со = 314 с-1, т. е. при вполне реальных для современных вибрационных уст­ройств значениях параметров, максимально возможная передаваемая мощность составляет около 800 кВт.

4. Установление определенных соотношений между фазами вращения роторов. В устойчивых синхронных движениях возбудителей устанавливаются некоторые вполне определенные значения относительных фаз вра­щения роторов а, — а%. В ряде случаев, особенно при большом числе возбудителей, таких устойчивых (в ма­лом) фазировок может быть несколько. Каждой устой­чивой фазнровке соответствует определенный закон дви­жения колебательной части системы, т. е. несущих тел, на которых установлены роторы.

5. Интегральный признак устойчивости (экстремаль­ное свойство) синхронных движений. В случае самосин­хронизации дебалапсных вибровозбудителен с одинаковы­ми парциальными скоростями вдали от резонанса и при малой диссипации энергии в линейной колебательной си­стеме устойчивые в малом фазировки соответствуют точ­кам грубого минимума относительно разностей фаз а, — ak средней за период функции Лагранжа колеба­тельной части системы, вычисленной в соответствующем приближении. Во многих других случаях устойчивые фа­зировки соответствуют точкам грубого минимума несколь­ко более сложной по структуре функции разностей а, — ~ак — так называемой потенциальной функции D.

6. Эффект взаимного уравновешивания роторов при их установке на мягко виброизолиро ванном твердом теле (принцип минимума средней кинетической энергии). Предположим, что вибровозбудители установлены на твердом теле, которое связано с неподвижным основа­нием столь мягкими упругими элементами, что частоты свободных колебаний тела значительно ниже синхронной скорости а. Тогда потенциальной энергией тела можно пренебречь по сравнению с кинетической, и если, к тому же, возбудители обладают одппаковыми положительными парциальными угловыми скоростями, то из интегрального критерия устойчивости вытекает, что устойчивым син­хронным движениям будут соответствовать минимумы среднего за период значения кинетической энергии тела. Иными словами, устойчивыми будут такие фазировки роторов, при которых неуравновешенные силы и момен­ты, ими генерируемые, взаимно компенсируются в том смысле, что усредненная за период кинетическая энер­гия принимает минимальное значение. В частности, если возможна такая фазировка, при которой имеет место полная взаимная компенсация неуравновешенных сил и моментов, то именно эта фазировка (которой со­ответствует нулевое значение кинетической энергии тела) и является устойчивой; тело при этом практи­чески не совершает колебаний (см. рис. 12.6, в, 12.7, а и 12.8, а). Указанную фазировку назовем компенси­рующей.

Заметим, что данную закономерность можно рассмат­ривать как своеобразное обобщение известного принципа Лаваля, состоящего в самоуравновешпвании диска, сидя­щего на гибком валу, в послекритической области частот вращения. О практическом использовании эффектов, свя - ванных с описанной закономерностью, рассказывается в раздело И.

7. Парадикс неработающих связей. Как следует из изложенного в п. 6, при самосинхронизации вибровозбу­дителей с одинаковыми положительными парциальными скоростями могут существовать и быть устойчивыми синхронные движения, в которых несущие тела (или тело) в синхронном движении остаются неподвижными (см. рис. 12.6, в, 12.7, я и 12.8, а). Создается иллюзия, что колебательпая часть системы в этих случаях не вы­полняет никаких функций и вовсе не пужна для синхронизации. На самом деле это не так: при случай­ном возмущении движения, например при изменении какой-либо из фаз а„ возникают колебания несущих тел, которые не прекращаются до тех пор, пока возмущение не затухнет.

Описанный эффект характерен для самосинхрониза­ции не только вращающихся, по и колеблющихся объек­тов. Впервые он был описап X. Гюйгенсом, наблюдавшим самосинхронизацию маятниковых часов [35, 42, 89].

8. Зависимость характера устойчивой фазировки воз­будителей от числа степеней свободы колебательной си­стемы (несущих тел). Характер устойчивой фазировки вибровозбудителей может измениться при изменении чис­ла существенных степеней свободы несущих тел. Так, например, присоединение к несущему телу дополнитель­ного груза на пружине или маятника и т. п. может при­вести к тому, что устойчивое синфазное вращение роторов стапет неустойчивым, а неустойчивое противофазпое — устойчивым, и наоборот (рис. 12.7). Подобным образом характер устойчивой фазировки возбудителей обычно ме­няется при переходе угловой скорости м из одного диа­пазона между частотами свободных колебаний несущих тел, а также некоторыми другими разграничительными частотами в соседний диапазон (см. также раздел 14).

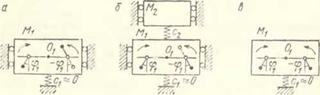
9. Парадокс принуждения. Для иллюстрации этого парадокса, а также предыдущей закономерности рассмот­рим следующий пример. Пусть необходимо обеспечить прямолинейные поступательные колебания мягко вибро - изолированного твердого тела по закопу, близкому к гар­моническому (рис. 12.7). Для этой цели могут быть ис­пользованы два одинаковых дебалансных вибровозбуди - телп с роторами, вращающимися в противоположных направлениях. Для гарантии колебаний тела в нужном направлении па первый взгляд представляется полезпым

поместить тело в паправляющие (рпс. 12.7, а). Однако, как показывает исследование (см. пример в и. 12.3.5) и гледует из изложенного в п. 6, в этом случае возбудители будут устойчиво самосинхронизироваться с таким соотно­шением фаз, при котором вынуждающие силы, развивае­мые возбудителями, взаимно уравновешиваются, а тело останется практически пеподвижиым (эта фазировка по­казана на рпс. 12.7, а сплошными линиями). Требуемая же фазировка (показанная штрихами) является неус­тойчивой.

Исследование показывает, что существуют по крайней мере два способа обеспечения устойчивости требуемой фазировки: либо присоединить к основному телу по­средством пружины некоторое добавочное тело *) (рис. 12.7,6), либо, как это ни кажется парадоксальным, просто убрать направляющие (рис. 12.7, в). Можно, ко­нечно, сказать, что в обоих случаях желаемый результат достигается одним и тем же способом — изменением чис­ла степеней свободы колебательной части системы. Таким образом, данный парадокс тесно связан с закономер­ностью, описанной в п. 8.

10. Зависимость характера устойчивой фазировки от числа возбудителей. Добавление одного или нескольких возбудителей может существенно изменить характер их устойчивой фазировки при самосинхронизации. Это яв­ствует, например, из сопоставления условий устойчивости

*) Естественно, что жесткость пружины, массы тел и частота

о) должны при этом удовлетворять некоторому неравенству (см. [35, 42]).

синфазпого сращения двух и трех симметрично располо­женных роторов в п. 1 и 5 табл. 1.

11. Зависимость характера устойчивой фазировки от относительных направлений вращения роторов возбуди­телей, Представление об этой закономерности дает п. 1 табл. 1. Исключение представляет простейшая си­стема, рассмотренная в примере п. 12.3.5 (вибрационпые моменты в этом случае не зависят от чисел Оі и а2, ха­рактеризующих направления вращения роторов).

Все закономерности и парадоксы, о которых говори­лось в настоящем разделе, широко используются в на­стоящее время нри создании новых и совершенствовании существующих вибрационных машин и устройств; на них основано много важных изобретений. Вместе с тем, как уже отмечалось, возможности использования своеобраз­ных закономерностей самосинхронизации еще далеко не исчерпаны.