Разделение частиц в слое сыпучего материала под действием вибрации (сегрегация, самосортпрование)
Разделение частиц в слое материала под действием вибрации используется и как самостоятельный процесс, и как составная часть более сложного разделительного процесса, например, в грохотах, о которых говорилось выше, а также в концентрационных столах, отсадочных машинах и других устройствах.
Некоторые закономерности разделения в слое, называемого также сегрегацией и самосортированием, схематически представлепы на рис. 7.2. При отсутствии вибрации находящаяся в сосуде смесь разнородных частиц сыпучей среды в поле силы тяжести или другом стационарном силовом поле может иметь вследствие действия сил типа сухого тронпя бесконечное число непрерывно
|
|
|
S |
|
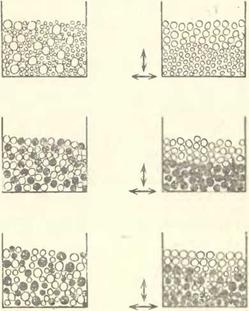
Рис. 7.2. Под действием горизонтальной симметричной или вертикальной вибрации сосуда с сыпучей смесью происходит разделение частиц по крупности и плотности (сегрегация, самосортированне): а) в случае смеси крупных и мелких частиц одинаковой плотности в результате вибрирования крупные частицы располагаются над мелкими; б) в случае смеси тяжелых и легких частиц одинаковой крупности легкие частицы располагаются над тяжелыми; в) в случае смеси крупных и мелких частиц двух различных плотностей нижнєє положение займут мелкие тяжелые, затем расположатся мелкие легкие, крупные тяжелые (или смесь мелких легких и крупных тяжелых); в верхнем положении окажутся крупные легкие частицы |
|
в |
а
распределенных положений равновесия: она расдолага - ется так или почти так, как ее засыпали в сосуд. Если же подвергнуть вибрированию (не слишком интенсивному, чтобы не преобладала хаотическая компонента процесса, т. е. перемешивание — см. раздел 8), например, смесь крупных и мелких частиц одной плотности, то в результате воздействия вибрации крупные частицы рас -
ния ю = о, щ соответствующего наибольшему ускорепию Лю2, при котором смесь еще движется вместе с сосудом. Описанная зависимость похожа па резонансную кривую, однако, как явствует из изложенного и будет показано
|
5 Wz0,mm/c
|
|
|
|
|
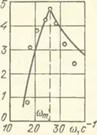
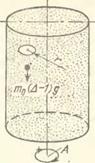
Рис. 7,4. Псевдорсзоиапсный эффект: спорость погружения или всплывания частицы, отличающейся по плотности от плотности сыпучей среды, находящейся в вибрирующем сосуде, имеет отчетливый максимум при некоторой частоте вибрации а>т; этот эффект используется в машинах для очистки зерна от минеральных примесей: а) схема системы; б) зависимость спорости погружения от частоты круговой горизонтальной вибрации сосуда (теоретическая кривая и экспериментальные точки)
|
|
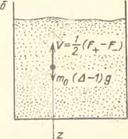
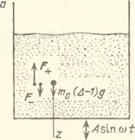
Гис. 7.5. При определенных условиях тяжелая частица (например, стальной шарик) всплывает в менее плотной среде, помещенной в вертикально вибрирующий сосуд (например, в песке): о) схема системы, б) наблюдатель V объясняет этот эффект возникновением дополнительной выталкивающей вибрационной силы V, обусловленной ббльшим сопротивлением движению частицы в направлении дна, чем в направлении свободной поверхности (силовая асимметрия) — см, рис. 4,1, 1, 3
ниже путем более обстоятельного анализа, таковой не является: «пиковый» характер зависимости связап здесь со своеобразной пгрой сил типа сухого трения и
пперцпи. Поэтому рассмотренный эффект и можно назнать псевдорезонансным. Он используется, в частности, її машппах для очистки зерна от близких по размерам минеральных частиц. При случайном попадании таких примесей в поступающее на помол зерно испеченный из муки хлеб весьма неприятно хрустит па зубах.
2. Эффект всплывания тяжелой крупной частицы в слое легких мелких [30, 31]. Объяснение этого эффекта непосредственно следует из изложенного в п. 2.3.2 и 4.2, если учесть, что сопротивление среды движению крупной тяжелой частицы вппз больше сопротивления ее движению вверх, особенно вблизи дна сосуда. В результате возникает вибрациопная спла, направленная в сторону меньшего сопротивления, т. е. вверх. Если эта вибрационная снла больше веса частицы в среде, то частица всплывает, несмотря на то что опа плотнее частиц среды (см. рис. 2.2, 4.1 и 7.5). Этот эффект служит основным подтверждением неприемлемости «потенциальной» теории вибрационного разделения сыпучих смесей, о которой говорилось выше.
Теория рассматриваемых процессов еще далека от завершен шш. В общей форме ее основная задача может быть сформулирована следующим образом. Имеется сосуд со смесью частиц, различающихся по крупности, плотности и другим параметрам, совокупность которых обозначим через а. Заданы закон колебаний точек поверхности сосуда, поле внешних сил и средняя за период колебаний плотность распределения / (я, у, г a; fQ) частиц но параметрам в каждой точке сосуда в некоторый начальный момент «медленного» времени і о. Необходимо найти плотность распределения J [х, у, z, a, t) в любой момент времени f; в частности, особый интерес представляет конечное распределение I* (х, У, 2; о) = lim / (х, у, г; а t). Возможна и более простая по - /->00
гтаповка задачи, когда смесь характеризуется некоторым набором классов частиц Ьі, ..., 6*. Задаются начальные концентрации с і (а", у, z, k), ..., Ch(x, у, z, t0) частиц каждого класса и требуется найти их значения в произвольный момент времени г > t0 и, п частности, предельные значения с*, ..., при t-*-oo. В насто - лщее время рассмотрен лишь ряд весьма частпых случаев поставленной общей задачи, соответствующих, папример, ситуации, когда концентрации интересующих исследователя частиц си...
..ck-1 столь малы по сравнению с концентрацией частиц некоторого класса с* («среды», «постели»), что можно не учитывать (или учитывать приближенно) взаимодействие частиц первых к — 1 классов и рассматривать движение изолированных частиц отих классов в среде иэ частиц «постели». При этом наряду с детерминистическим (см. ниже, а также работы [51, 78, 79, 238а]) используется рассмотрение процесса как случайного; в последнем случае математической моделью служат уравнения тппа уравнении диффузии или КолмогороваФоккера — Плапка [161], Нв«
достатйом пёрвогб подхода является неучет случайных факторов, а второго — трудности в установлении функциональной зависимости параметров, входящих в дифференциальные уравпепия случайного процесса, от нарамотров вибрации. Попытка сочетания указанных подходов п учета взаимодействия отдельных классов разделяемых частиц сделана в работе [31].