Примеры нахождения вибрационных сил и составления уравнений медленных движений (основных уравнений вибрационной механики)
1.1.1. Предварительные замечания. Прежде чем рассмотреть вопрос о получении основных уравнений вибрационной механики в общей математической форма (п. 2.4), приведем несколько простых, по важных в прикладном и принципиальном отношепни частных примеров. На этих примерах будет выяспеп физический механизм возникновения вибрационных сил и проиллюстрированы эвристические, полуинтуитивные приемы получения их приближенных выражений. Впрочем, нам неизвестны случаи, когда такие нестрогие приемы при осмотрительном их примепепии приводили бы к серьезным ошибкам. В сущности, эти приемы содержат два основных элемента: 1) приближенное пахождение быстрого движения при простейших предположениях (как правило, в так называемом чисто инерционном приближении, справедливом при достаточно высокой частоте и интенсивности быстрых сил); 2) вычисление вибрационной силы при указанных быстрых движениях, сводящееся к простому усреднению, т. е. к вычислению некоторых определенных интегралов. При я? елании читатель может легко рассмотреть то же примеры более строго — следуя общей методике, изложенной в п. 2.4, или же обратиться к имеющейся литературе (см. п. 2,6).
На приводимых примерах будут рассмотрены также некоторые из упоминавшихся нелинейных эффектов, используемых в вибрационной технике и технологии.
1.1.2. Движение тела по шероховатой плоскости под действием продольной гармонической вынуждающей силы (простейшая модель процесса вибрационного перемещения). Рассмотрим тело массой т, лежащее на горизонтальной шероховатой плоскости, на которое действует горизонтальная сила Ф0 sin cot с амплитудой Ф0 и частотой со (рис. 2.2, а). Если коэффициенты сухого трения при скольжении тела вперед и назад по плоскости /+ и /_ одинаковы и равны /, то ясно, что при Ф0 < mg} тело останется неподвижным, а при Ф0 > mgf будет совершать симметричные колебания относительно некоторого среднего ПОЛОЖЄНИЯ. Если же допустить, например, что /_ > /+, то симметрия нарушится, и, как видно из рассмотрения характеристики силы сухого трения F на рис. 2.2, а, при Ф0 > mgf+ тело будет перемещаться в положительном направлении (в случае /_ < /+ при Ф0 > > mgf - будет иметь место перемещение в отрицательном направлении, т. е., как и ранее, в направлении, в котором сила сопротивления меньше[3]). Действительно в течение некоторого промежутка времени первого полупериода 0 < cot < я, когда Ф0 sin cot > mgf+, тело сдвинется вправо, а в течение второй половины периода я < cot < 2л, когда Ф0 sin cot < 0, либо останется на месте (если Ф0<mgf~), либо сдвинется влево на меньшее, чем вправо, расстояние, поскольку сопротивление движению влево больше, чем сопротивление движению вправо. Таким образом, за каждый период изменения силы будет происходить пекоторое смещение тела вправо. Наблюдатель V, не замечающий быстрой силы Ф0 sin cot и силы сухого трения, которая также изменяется «быстро», припишет движение тела вперед появлению некоторой силы — вибрационной силы V, действующей в положительном направлении (см. рис. 2.2, б). Эта сила, в частности, может обеспечить движение тела даже вверх по плоскости, т. е. против силы тяжести, если наклонить плоскость на некоторый не слишком большой угол.
Подсчитаем впбрациоппую силу приближенно, хотя в даппом случае задача допускает достаточно простое точное решение. Л пмеппо, рассмотрим быстрое движение тела в чисто инерционном приближении, т, е, при нахождении быстрого движения будем учитывать только быструю силу Ф0 sin <of, а силой сухого трения (тоже быстрой!) пренебрежем; естественно, что это предположение будет тем точнее, чем больше Фо по сравпепию с mgf+ п mgf— Тогда, согласно второму закопу механики, уравпение быстрого движения будет иметь вид (здесь и везде далее мы предполагаем, что движение системы представимо в виде (2.2))
mif> = Ф0 sin cof, (2.4)
и ого периодическое решение получится простым двоипым интегрированием
|> =» — A sin со[4] зз A sin (cof + л) ( /1 = % )• (2.5)
moo /
Иными словами, в рассматриваемом приближении быстрое движение будет представлять собой гармопическое колебание с частотой со и амплитудой А = Ф0/(та)2), противофазное по отпо - шеппю к силе Фо sin cof; нетрудно попять, что эта последняя закономерность характерна для чисто инерционного приближения.
Теперь легко подсчитать средпюю за период силу трепия F(mi), действующую на тело при указанном движении. Эта сила и будет в данном случае представлять собой вибрационную силу *)
2Я
(2.6)
о
Предположим сначала, что медлепная составляющая движепия тела отсутствует, т. е. X = 0, так что х = г|з = —.4cocos cof. Тогда (рис. 2.2, в) в течение полупериода '/2я < соf < 3/2л тело движется вправо по плоскости (х > 0) и сила трепия F = F+ = = —mgf+ < 0 направлена влево. В течение друюго полупериода 3/гл < cof < 5/2Л тело движется влево (і < 0) и сила F = F - => ■= mg]- > 0 направлепа вправо. Поэтому (Т = 2я/со)
v (0) = <^>|i=o = т (- mSf+ Т + msf~ т) = Т mg V - ~ /+)•
(2.7)
Ненамного сложнее вычисление силы в случае, если тело, помимо колебаний но закону (2.5), движется с некоторой постояыпой
или медленно изменяющейся скоростью X. Тогда (см. рис. 2.2, г)
v(x)=<F> = £lmg(f_t_-f+t+), (2.8)
где t+ и f_ — промежутки времепп, в течение которых тело движется соответственно вправо п влево по плоскости, причем
coi, «= 2 I л — arccos - Д. ], cof_ [5]= 2 arccos —. (2,9)
+ Аа> j Лш
С учетом отих выражепий формула (2.8) приобретет вид
![]()
|
V(X) = <F> = ^ |
|
(2.10) |
jr
(/++/_) arccos^-/+n
При X = 0 эта формула, как и должпо быть, совпадает с (2.7).
Своеобразная зависимость вибрациоппой сплы V от скорости X, соответствующая формуле (2.10), изображопа на рис. 2.2. б. К обсуждению этой зависимости, характеризующей эффект кажущегося превращения под действием вибрации сухого трения в вязкое (эффект псевдоожижения), мы еще обратимся в п. 4.4 и 6.3*).
При учете формулы (2.10) уравнение медлеппого движения (2,3) запишется в виде
X = l!±(f+ +— arccos А. - А (2.11)
л [ f+ A at )
Приравппвая правую часть этого уравпепия пулю, получаем выражение для скорости установившегося движепия тела
л/, Ф л /.
*0 = A(S) cos /+ + /_ = пш со® /+ 4- /_* (2>12)
•
При /+ = /_, как и должпо быть, Ха = 0, т. е. тело «в среднем» остается неподвижным, совершая лишь быстрые колебания относительно некоторого среднего положепия. Следует, конечпо, иметь в виду, что от формул (2.10) — (2.12) пужпо ожидать тем большей точпости, чем больше амплитуда силы Ф0 по сравпеппго с максимальным значением силы трения F = mgf-. Отметим также, что эти формулы остаются справедливыми и в случае, когда па тело пе действует выпуждающая сила Ф0 sin соt, а плоскость, па которой опо лежит, совершает гармонические колебаппя с амплитудой А и частотой м.
1.1.3. Частица в быстро осциллирующем неоднородном поле. В качестве второго примера, который, также как и первый, относится к одной из базовых моделей изучаемых явлений, рассмотрим поведение частицы в ста-
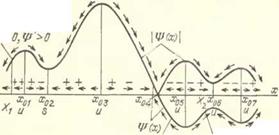
ционарпом быстро осциллирующем поле, амплитуда которого IV(х)I изменяется по некоторой пространственной координате х, т. е. быстрая сила носит характер так называемой стоячей волны (рис. 2.3, а). Точки х, где Ч' (ж) = 0, называют узлами, а точки х, где Ч7 (х) имеет максимумы или минимумы,— пучностями волны (в таких точках 4;'(ar)=0). На частицу может действовать также не зависящая от времени сила F(x). Будем считать, что на расстояниях порядка амплитуды колебаний частицы силы F (х) и Ч7 (х) изменяются не слишком сильно.
Уравнение движения частицы имеет вид
|
(2.13) |
mx — F (х) + Ч; {х) sin at.
Здесь, как и выше, т — масса частицы, а а — частота осцилляции. К изучению описанной модели сводится классическая задача о поведении маятника с вибрирующей осью, а также ряд задач о дрейфе частиц в акустических и электромагнитных полях.
Как и в первом примере, приведем вначале качественное рассмотрение задачи на полуиптуитивном, как иногда говорят, эвристическом уровне. Предположим, что частица находится вблизи некоторого положения х = А", и совершает относительно него быстрые колебания |з, обусловленные действием силы Ч; (.г) sin at; если эти колебания действительно быстрые, а амплитуда силы Ч7 (х) достаточно велика по сравнению с медленной силой F(x), то за один период колебаний Т = 2л/со среднее положение частицы не успеет сколько-нибудь заметно сместиться. При этих условиях, как и ранее, быстрые движения частицы можно найти из уравнения
|
(2.14) |
= Ч; (.Yi)sin at,
т. е. ограничиться при рассмотрении таких движений чисто инерционным приближением. Как и в первом примере, быстрое движение
|
|
будет представлять собой гармоническое колебание, противофазное по отношепию к силе Чг (A"i)sin at. Эта общая закономерность существенна. Действительно, пред-
|
|
|
|
|
V(x),VCx) |
|
t>t |
|
|
t
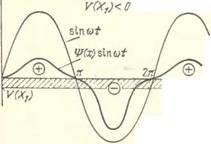
положим, что в рассматриваемой точке х = Х справедливы неравенства Ч/(Хі)>0, Чг'(Хі)>0, т. е. функция Ч/(з:), будучи положительной, возрастает (рпс. 2.3, г). Тогда за одну половину периода 0 < cot < л, когда сила 4r(;z)sinco£ положительна, среднее значение <Ч; (x)sin 0)<>г/2 этой силы будет по абсолютной величине меньше, чем среднее значение той же силы за другую половину периода, когда эта сила отрицательна. В результате среднее значение силы Ч; (a;) sin at за период окажется отрицательным: F(Xi) =<ЧГ (a:)sin at)< 0. Аналогичным образом легко устанавливается, что если быстрое движение происходит вблизи точки X = Х2, в которой Ч/(Х2)<0 п Ч/,(А'2)>0, то (см. рпс. 2.3, д) V(XZ) = = <Ч/ (x)sin at» 0. И вообще, если в некоторой точке х — Хп знаки V (Хп) и ^'(Х,,) одинаковы, то F(Xn)<0, а если эти знаки различны, то F(Xn)> 0.
Эта закономерность иллюстрируется рпс. 2.3, в, где первый знак па определенном интервале изменения функции (х) соответствует знаку Ч/(а:), а второй — знаку Ч/,(а;). Стрелками над осью абсцисс и над графиком функции Ч/ (х) указаны направления действия вибрационной силы V (X).
Из рассмотрения рис. 2.3, в следует и другая весьма важная закономерпость: в результате действия силы ^(arjsinmf возникает медленная сила V, всегда «притягивающая» частпцу к точкам минимума функции І Чг (х) I и «отталкивающая» ее от точек максимума этой функции. Иными словами, вследствие действия силы xF(a;)sina)t частицы будут медленно двигаться («дрейфовать») к точкам минимумов функции |Чг(д:)| как к некоторым устойчивым состояниям квазиравновесия. В числе таких устойчивых точек (па рпс. 2.3, в опи помечены буквой «s» в отличие от неустойчивых точек, помеченных буквой «и») будут и точки, где VF (х) = 0, т. е. узлы волны Ч' (х).
Конечно, при наличии медленной силы F(x) положения квазиравновесия частицы могут сместиться, изменить свой характер и даже совсем исчезнуть. Установленная закономерность в этих случаях проявляется лишь в виде тенденции.
Изложенный качественный вывод, а также простая формула для вычисления вибрациоппой силы могут быть легко получены аналитически. Действительно, вблизи точки х = X амплитуда силы (х) может быть приближенно представлена в виде
Т (х) = V (X ir Ч>) = ¥ (*) + ¥'(*)*. (2,16)
Но тогда прп учете выражения (2.15) и равенств [6]) <sin со<> = 0, <sin2 cot) = ~2
|
(2.171 |
легко находим
|
V (X) = (У (я) sin сог> =
|
1 Y (X) У' (X)
2 ото2
(2.18)
Отсюда непосредственно усматривается сформулированный выше качественный результат.
Замечая, что У (X) У (X) = — [У2 (X)]', выражение для вп-
|
(2.19) |
брационпой силы можно представить в форме
где положено
|
|
|
= - J - mA2 (X) ша |
(2.20)
и учтено обозначение (2.15).
Из равенства (2.19) следует, что вибрационная сила V связана с функцией Пу точно таким же образом, как обобщенная сила с потенциальной энергией системы. Если ввести теперь еще и «обычную» потенциальную эпергпю По, соответствующую медленной силе Р
|
|
(2.21)
то уравпеппе медленных движений представится в виде (напомним — см. также п. 2.4,— что это уравнение представляет собой результат усреднения исходного уравнения (2.13) и что в линейном относительно i|) приближении <F(x)> = F(X)) [7])
all
|
(2.22) |
mXz=~7x (n==no + nv)>
где через П обозначена полпая потепцпальпая эпергпя медлеппых движений частицы.
Полученные формулы, как нструдпо убедиться, вполпе согла - суются с выводом, который был сделап выше па оспово качественных рассуждепий. Действительно, если медлеппая сила F(x) отсутствует, то можно положить По = 0 и П = П^. Но, согласно теореме Лагранжа — Дирихле, точкам минимума потенциальной энергии П = Пу соответствуют точки устойчивого равповеспя системы. Как следует из выражения (2.20), эти точки совпадают с точками минимума функции [^(я)]2, пли, что то же, с точками мипимума функции | (а:) |, как и было установлено ранее.
Обратим внимание на весьма примечательпое обстоятельство, полученное в результате проведенного рассмотрения: исходная система, описываемая уравпепием движения (2.13), была существенно некопсервативпой, тогда как уравнение медленного движения (2.22) соответствует консервативной системе. С такими «потенциальными в среднем* системами мы еще столкнемся ниже, при рассмотрепии явлеппя самосинхронизации неуравновешенных роторов (раздел 12). Для этих систем, как и для рассмотренной выше, существует некоторая функция D, называемая потенциальной функцией, которая играет ту же роль, что и потепцпальная энергия в консервативных системах: точкам мипимума этой функции соответствуют устойчивые положения равновесия или устойчивые движения системы.
Заметим в заключение, что выражение (2.20) для потенциальной энергии вибрационпой силы Пу может быть, согласпо (2.15), представлено в форме
Пу = ^ тЛ2 (X) о)2 = ^~2" = <7», (2.23)
где Tv — кинетическая эпергпя частпцы в ее быстром движения. Поэтому формулу (2.22) для полной потенциальной энергии медленного движения П можно записать в виде (учитываем, что <По) = По)
П = <П„ + Ту>. (2.24)
Обратим внимание на прпмечательпый эффект, вытекающий пз приведенных простых рассуждений и выкладок: при отсутствии осцилляции частица может не иметь положений устойчивого равновесия, а при их наличии положеппп устойчивого квазиравпове - спя могут появиться. Действительно, уравнение F(x) =0 может не пметь вещественных корней, для которых F'(x) < 0, а уравнение F(X) + V(X) =0 может иметь соответствующие корни (или, что то же. функция П3(і) может не иметь минимумов, а функция П(Х) = По(Х) - f-IIv(A’) —иметь таковые). Иными словами, осцилляции могут приводить к появлению точек локализации частиц — «потепциальпых ям». Применительно к движению заряженных частиц в высокочастотных электромагпитпых полях этот п подобные аффекты рассмотрены в работах [66, 67, 150] (см. также п. 2.6),
1.1.4. Маятник с вибрирующей осью подвеса. Задача о маятнике с вертикально вибрирующей осью подвеса (рис. 2.1, б) представляет собой частный случай задачи, подробно проанализированной в предыдущем пункте, Действительно! дифференциальное уравнение движения
такого маятника имеет ішд
/ф + ml (g + А ш2 sin cot) sin ф = 0, (2.25)
Оно отличается от классического уравнения колебаний маятника с неподвижной осью лишь тем, что к ускорению земного тяготения g добавлено ускорение вибрации (обозначения здесь те же, что и в п. 2.1). Сопоставляя это уравнение с (2.13), заключаем, что в данном случае можно положить
F(t)= — mgl sin ф, ^(ф)^ — m^co’Zsin ф, (2.26)
причем роль координаты х играет угол поворота маятника ф.
|
|
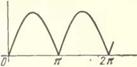
Согласно изложенному в п. 2.3.3, «точками притяжения» маятника, обусловленными действием вибрации, будут точки минимума функции I *¥ (ф) I = тАыЧ [sin фI. Таких существенно различных точек всего две: фі = 0 и ф2 = я (рис. 2.4); первая соответствует пижпему, а вторая — верхпему положению маятника. Если сила
тяжести отсутствует (F = 0) или., „
«____ Рис. 2.4. График функции
мала по сравнению с силои ппер - fein фі
цип тоЛш2, то этим точкам и соответствуют положения устойчивого равновесия маятника— маятник располагается вдоль направления вибрации. В другом крайнем случае, когда mAml<g, как хорошо известно, нижнее положение фі == 0 устойчиво, а верхнее неустойчиво.
Чтобы получить условие, при выполнении которого вибрация стабилизирует верхнее положение маятппка, достаточно выписать выражения для вибрационного момепта V (а) пли для полной потенциальной эпергни медленного движения П(а) (а —медленная составляющая угла ф). При учете формул (2.18) —(2.22), в которых следует заменить величину т па /, а также равенств (2.26) находим
(тМш)г.
V (а) = —jj— sin 2а, (2.27)
_, . , , (ліМи)5
П (а) = mgl cos а + —— cos 2а, (2.28)
Уравнение медленного движения при этом имеет вид
(тМсо)2
/а + mgl sin а - f—-q—sin 2а = 0, (2.29)
т. е. отличается от обычпого уравнения колебаппй маятника наличием последнего слагаемого (вибрационного момента). Вблизи верхнего положения равновесия аз = л уравнение (2.29) заменяется линейным дифференциальным уравнением
, . і, . (mMm)*
|
а = 0, (2.30) |
Ja + — mgl+ —2у-
а вблизи нижпего аі = 0 — уравнением
/а + |mgl + — j а = 0. (2.31)
|
тА2Ш* 2 gJ |
Поскольку выражениям при а в этих уравнениях соответствует коэффициент жесткости с в уравпеппп колебаппй простейшего осциллятора тх + сх — 0, то, как уже отмечалось в п. 2.1, действие вибрации в данном случае приводит как бы к появлению вблизи обоих положений равновесия пружпп с поворотной жесткостью cv = (т/Лш)2/2/ (см. рис. 2.1, б). Для устойчивости, как известпо, с должно быть положительным. Если эта жесткость больше абсолютной величины «отрицательной жесткости» <^,2'= —mgl, обусловленной моментом силы тяжести при верхнем расположении маятника, т. е. выполняется условие
> I, (2.32)
то верхпее положеппе равновесия маятника будет устойчивым. Вблизи нижпего положения равповесия ai = 0 жесткость су добавится к положительной жесткости = mgl, что, как отмечалось, приведет к увеличению частоты свободных колебаний маятника вблизи этого положения (маятниковые часы вследствие вибрации всегда спешат).
Простое качественное объяснение рассмотренных эффектов приводится в кпиге [142].