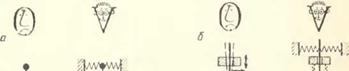Об асинхронном подавлении и возбуждении автоколебаний
В пастоящем разделе нельзя пе сказать о двух важных целиной них явлениях — явлении асинхронного подавления и асинхронного возбуждения автоколебаний [4, 136].
В первом случае автоколебательная система определенного вида, генерирующая устойчивые колебапия некоторого периода Т0 — «= 2л/(о0, при действии вынуждающей силы высокой частоты со > со0 и амплитуды, большей некоторого порогового значения, перестает генерировать автоколебания, а совершает выпуждепные колебания с высокой частотой со и относительно малой амплитудой.
Во втором случае нелипейная система определенного вида, пе геперирующая колебаний, в результате действия вынуждающей силы частоты ш начинает генерировать автоколебания некоторой значительно меньшей частоты ш0.
Оба явления просто трактуются с позиций метода прямого разделения движений. Как показывает простое исследование, на котором здесь, однако, пе будем останавливаться, в первом случае медлепное движение происходит так, как если бы в систему добавилось некоторое дополнительное вязкое сопротивление, зависящее от амплитуды и частоты вынуждающей силы. В результате «медленные» автоколебания подавляются. Во втором случае действие вынуждающей силы высокой частоты на медленное движение сводится к добавлению «отрицательного трения», в результате чего положение равповесия системы становится неустойчивым, и она начинает генерировать колебания.
Рассматриваемые нелинейные явления играют значительную роль в радиоэлектропике. Однако нам почти неизвестпы упоминания о них в механике или машиноведении. Высказанная в разделе 10 гипотеза об асинхронпом подавлении автоколебаний при вибрационном резании, а также гипотеза о возможной роли этого ппления в биомеханике (см. раздел 19), например в закономерностях автоматизма и резервирования в системе возбуждеппя ритма сердечпых сокращений [47], пока составляют исключения. Представляется, однако, что это положепие в будущем может
и. шепнться.
14. ВПБРЛЦПЯ СТАБІІЛИЗІІГУЕТ — ВИБРАЦИЯ ДЕСТАБИЛИЗИРУЕТ
В п. 2.3Л уже говорилось о том, что вертикальная вибрация осп подвеса маятника, частота которой значительно выше частоты его свободных колебаний, может стабилизировать— сделать устойчивым — его верхнее («опрокинутое») положение. Наблюдателю V представляется, что это происходит вследствие появления пекоторых невидимых пружин (рпс. 15.1, я).
|
|
|
-А, А Д. |
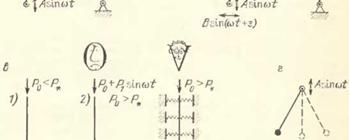
Рис. 15.1. Вибрационное воздействие может привести как к стабилизации неустойчивого положения равновесия системы или повышению запаса устойчивости, так и к дестабилизации устойчивого положения равновесия: а) вертикальная вибрация оси подвеса маятника при определенных условиях приводит к стабилизации его верхнего положения равновесия (см. также рис. 2.1, б и п. 2.3.4); б) шайба, свободно насаженная на стержень такого маятника, может быть стабилизирована вблизи некоторого положения квазиравновесия; е) 1— упругий стержень не теряет устойчивости прямолинейной формы равновесия под действием продольной силы Р, если последняя не превышает критического значения Р*; 2 — наложение вибрационной составляющей Pt sin со/ может позволить существенно повысить это критическое значение (справа на рисунках а) —
в) изображены картины, видимые наблюдателем V, которому представляется, будто стабилизация происходит вследствие наличия некоторых пружин); г) при определенных условиях, отличных от условий рис. а, нижнее положение равновесия маятника дестабилизируется колебаниями оси подвеса (явление параметрического резонанса)
Другой, более сложный эффект был обнаружен экспериментально В. Н. Челомеем [229]: шайба, свободно насаженная на стабилизированный указанным способом в опрокинутом положении стержень, начинает по нему подпи - маться вверх п также стабилизируется в определенном положении, совершая вблизи этого положения устойчивого квазиравновесия колебания малой амплитуды (рис. 15.1,6). Отметим два любопытных обстоятельства: 1) теоретический анализ описанного эффекта, выполненный почти одновременно и независимо разпыми исследователями [48, 147], не обнаружил возможности стабилизации шайбы при чисто вертикальных колебаниях оси подвеса стержня; в рамках выполненного анализа для этого оказывается необходимой также горизонтальная вибрация; тот же вывод вытекает из появившейся позднее работы [118]; 2) было обнаружено [48], что при наличии поперечных упругих колебаний стержпя, в отличие от частицы, находящейся в быстро осциллирующем неоднородном поле (см. п. 2.3.3), шайба может стабилизироваться не только вблизи узлов, но также и вблизи пучностей стоячих волн. Если второе обстоятельство легко объясняется, то первый факт еще не получил объяснения: не ясно, явилась ли стабилизация шайбы в опыте В. Н. Чело - мея результатом не замеченной им поперечной вибрации оси подвеса стержня либо результатом возникающих под действием продольной вибрации поперечных упругих или «твердотельных» колебаний самого стержня (естественно, что при чисто продольных колебаниях стержпя ни подъем, ни стабилизация шайбы невозможны). Последняя точка зрения (касающаяся твердотельных колебаний) отстаивается в работе [129], однако вопрос, как представляется, еще требует дополнительного рассмотрения.
Эффект вибрационной стабилизации опрокинутого ма - ятпика навел В. Н. Челомея на интересную мысль о возможности повышения устойчивости по отношению к постоянным или медленно изменяющимся силам (так называемой статической устойчивости) упругих систем с параметрическим возбуждением [228]. Им установлено, что статическая устойчивость может быть обеспечена даже тогда, когда статические нагрузки, действующие на вибрирующую систему, превосходят критические эйлеровы силы (рис. 15.1, в). Эти исследования были продолжены С. В. Челомеем [230].
Пример вибрациопной стабилизации частицы в быстро осциллирующем неоднородном поле был рассмотрен в п. 2.3.3. Как указывалось, ряд интересных эффектов стабилизации частиц в колеблющейся жидкости исследован в работах Р. Ф. Ганиева, Л. Е. Украинского и других ученых [61, т. 4; 63, 64].
Наряду со стабилизацией положепин равновесия плп движений динамических систем вибрация может оказывать и дестабилизирующее действие. Хорошо известно, что нижнее положение равновесия того же маятника с вертикально вибрирующей осью подвеса, устойчивое при отсутствии вибрации, становится неустойчивым в определенных диапазонах изменения частоты и амплитуды вибрации (см. рис. 15.1, г)—это так называемое явление параметрического резонанса (см., например, [4; 61, т. 2; 170-172])'.
Перечисленными случаями далеко не исчерпываются интересные проявления стабилизирующего и дестабилизирующего действия вибрации на механические системы. В частности, такие эффекты были обнаружены в поведении свободной поверхности жидкости, что открывает новые технологические возможности. Ряд результатов, относящихся к этому кругу явлений, и обзор иследовапий приводится в работе [18]. Явления асинхронного подавления и возбуждения автоколебаний, о которых говорилось в п. 14.3, также могут служить яркими примерами вибрационной стабилизации и дестабилизации положеиия равновесия.