О теории н расчете процессов вибрационного перемещения
Понятия о движущей вибрационной силе
и внбропреобразоваипой силе сопротивления
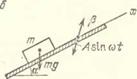
В качестве простейшей модели процессов вибрационного перемещения, описывающей ряд практически важных эффектов, рассмотрим движение тела (материальной частицы) массой т по горизонтальной плоскости, совершающей продольные колебания по некоторому заданному закону 1 = |(шt) с периодом 2я/со (левая часть рис. 4.14, а). Пусть па тело действует некоторая постоянная сила Т и сила сопротивления F, зависящая от скорости тела относительно плоскости х. Нетрудно видеть, что данная модель соответствует определенным вариантам силовой п кинематической асимметрии при возникновении вибрационного перемещения (рис. 4.1).
Дифферепциальпое уравпение относительного движения тела по плоскости запишется в форме
mx = Т— mi (at) + F(x). (4.3)
Уравпепие же медленного движения, т. е. движения, видимого наблюдателем V (правая часть рис. 4.14. а), легко получается способом, описанным в п. 2.4. Оно имеет вид
mX = Т +V(X), (4.4)
где
Г(А’) = (F(X-i)y (4.5)
— вибрационная сила, вычисленная в чисто иперциопном приближении (mg » F) л, как видно, в этом приближении представля
ющая собой результат осреднения за период 2л/ы силы сопротивления F(x), вычисленной при условии, что X = X — |.
Представим силу V в виде
V(i)-V(0) + 7,(i), (4.6)
F(0) = <F(-£)>,
F,(A) = (F(X-t Назовем составляющую вибрационной силы F(0) движущей вибрационной силой, а Vі(X)—вибропреобразованной [13]) силой сопротивления. Смысл такого расчленения впбрационпой силы состоит в следующем.
|
|
|
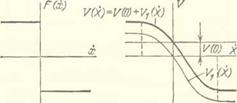
Рис. 4.14. Базовые модели процессов вибрационного перемещения: а) тело (материальная частица) на периодически колеблющейся горизонтальной плоскости при нелинейном законе сопротивления движению; б) тело (материальная частица) на наклонной шероховатой плоскости, совершающей гармонические прямолинейные поступательные колебания; s) эффект вибрационного преобразования силы сухого трения (псевдоожиже - пия); слева — разрывная характеристика силы сухого трения, справа — |
вибрационная сила V(X) и ее составляющие: движущая вибрационная сила V(0) и преобразованная сила сопротивления Vi(A')
Условием возникновения вибрационного перемещения является наличие пепулевого корня X = Х0 у уравнения
Т+ P(0) + Fi(X) =0, (4.8)
получающегося из (4.4) при X = 0 и при учете (4.6). В случав когда постоянная сила отсутствует (Г==0), из (4.8), поскольку I71 (0) =0, следует, что условием возникновения вибрационного перемещения является отличие от нуля движущей вибрационной силы:
F(0) = (F(-i)) ФО. (4.9)
В свою очередь, необходимым условием выполпепия этого соотношения является нелинеипость силы сопротивления F(x), ибо при F = к. г, где к = const, вследствие периодичности функции |(ffli). всегда 1(0) = 0. При иелппейпом законе сопротивления в случав Т — 0 вибрационное перемещение может быть обусловлено асимметрией либо закона колебаний плоскость £(шI) (кнпематическая асимметрия), либо силы сопротивления F(i) (силовая асимметрия), либо наличием той и другой асимметрии одновременно.
Следующий важный вывод из соотношений (4.7) состоит в том, что, несмотря на возможное паличне разрыва функции F(x) в точке х — 0 (это характерно для силы типа сухого трепия; см.
левую часть рпс. 4.14, в), зависимости Р(А') и Fi(X), вследствие операции осредпепия, являются непрерывными (см. правую часть рис. 4.14, в). Иными словами, для наблюдателя V происходит так называемое вибрационное сглаживание (преобразование) разрывной характеристики силы сопротивления. Сила сопротивления тина сухого трепия при этом преобразуется в силу типа вязкою
трепня Vi(A') (согласно (4.7) Fi (0) = 0) и в движущую вибрационную силу Г(0), как раз и вызывающую вибрационпое перемещение [14]).
Мы описали здесь одни пз простейших, по важных впброрео - логи чесних эффектов, о которых более подробно говорится в п. 6.3.
Естественно, что перемещепие тела по плоскости может быть обусловлено и силой Т. При сопротивлении типа сухого трения здесь одной из наиболее практически важных является следующая ситуация: при отсутствии вибрации сила Т недостаточна для обеспечения впбрациопного перемещения, поскольку она по модулю меньше предельной ВСЇЇИЧШШ силы статического трения, тело при этом покоится; при наличии же вибрации достаточной интенсивности сухое трепне «преобразуется в вязкое», так называемая зона нечувствительности исчезает и сила Т совместно с V'(0) обеспечивает течение процесса. Этот случай особенно важен, например, в обогащении полезных ископаемых, где вибрация, производя «разжижепие» сыпучей среды пли структурированной суспензии, открывает возможпость для проявления действия слабых разделяющих факторов. Нетрудно заметить, что аналогичная картина характерна для процесса вибропогружепня свай или шпунта, описанного в п. 4.3.4, а также для ряда процессов внбротрапспор- тпроваппя.
Подробггое исследование даппой модели приведепо в работах [37, 40].
Рассмотрим теперь более сложную модель — движение тела (материальпой частицы) массой т по шероховатой плоскости, наклопеппой к горизонту под некоторым углом а и совершающей прямолинейные поступательные гармонические колебания под углом (1 к плоскости с амплитудой А и частотой ш (рис. 4.14, б). Важная особенность этого случая состоит в том, что при значении «параметра перегрузки»
Лш2 sin р, ,,
w =---------------- >1 (4.10)
g cos а '
(г* — ускорение земпого тяготепия), т. е. когда проекция силы инерции на пормаль к плоскости больше соответствующей проекции веса тела, непременно имеют место режимы движения тола с отрывом тела от плоскости.
Как отмечалось в п. 4.3.1, по схемам, соответствующим даппой модели, работает большинство современных трапспортпых и трапспортно-технологическпх вибрационных машпп. Это объясняется - с одной стороны, относительной простотой во:ібуждепия гармонических колебаний, а с другой — достижимостью при данном
способе вибрационпого перемещения зпачительпых средних ско
ростей движения тел (порядка 1 м/с), а также транспортирования материала вверх под сравнительно большими углами (до 30° и вытпе).
Описанпые модели являются базовыми в теории процессов вибрационного перемещения — они играют здесь столь же важную роль, как модель маятпика (осциллятора) в теорип колебапий. В пастоящее время можно считать, что обе эти модели достаточно хорошо изучены точными методами; создапы также специальные программы для расчетов на ЭВМ [6, 30; 61, т. 2 и 4; 73, 131, 157, 207]. Тем не мепее использование понятия о вибрациоппой силе оказывается целесообразным как в связи с удобством интерпретации результатов, так и для приближенного анализа более сложных задач,"точное решение которых не представляется возможным (см., например, п. 6.6).