Неуравновешенный ротор в колебательной системе с диссипацией энергии. Эффект Зоммерфельда
Рассмотрим сначала первый случай (рис. 13.1, а]. Тормозящее действие вибрации основания, на котором установлен неуравновешенный ротор, легко понять. При наличии в колебательной системе демпфирования (а реально оно всегда есть) двигатель должен затрачивать энергию но только на преодоление момента сопротивления в подшипниках ротора, но и на поддержание вызываемых им колебаний. Весьма важен и любопытен, однако, характер этой дополнительной нагрузки на двигатель, определяемый выражением для вибрационного момента V. В простейшем случае, когда ротор установлен на платформе с одной степенью свободы,
y-rw—affiVtv+fa.. <‘«>
Здесь тп — масса ротора, е — его эксцентриситет, со — средняя частота вращения, М — масса системы, Х = р/со, где р = Vc/Л/ — частота свободных колебаний платформы при заторможенном роторе, с — жесткость упругого элемента, ге=р/(2Мю), р — коэффициент вязкого сопротивления колебаниям.
На рис. 13.1, а, 3 изображены зависимости R(a) — — У(со) и L(a>), где £(со) и 7?(ю) — соответственно вращающий момент и момент сопротивления вращению ротора при его установке на неподвижном основании, приведенные к валу ротора. Из рисунка и непосредственно из формулы (13.1) видно, во-первых, что вибрационный момент, как и следовало ожидать, всегда является тормозящим и, во-вторых, что его зависимость от частоты вращения носит ярко выраженный резонансный характер: IF (и) I имеет максимум вблизи со » р.
Существенно п на первый взгляд парадоксально, что этот максимум тем больше, чем меньше безразмерный
коэффициент демпфирования п иными словами, тормозящее действие вибрации может быть тем большим, чем меньше демпфирование в колебательной части системы. Однако отмеченная закономерность становится попятной, если вспомнить, что резонансные амплитуды колебаний также возрастают с уменьшением п, а выражение (13.1) для вибрационного момента можно представить в виде
F (со) =—j - FA cos у, (13.2)
где F = тесо! — неуравновешенная сила, развиваемая ротором, А = те/М [(1 — X2)2 + 4/г2],/г — амплитуда колебаний платформы, cos к = п/[({ — X2)2 + 4/г2]1/2, причем у есть сдвиг фаз между вынуждающей силой и колебаниями. Заметим, что формула (13.2) согласуется со сказанным в п. 12.3.4 об оценке величины вибрационного момента.
Продолжим рассмотрение рисунка 13.1, а, 3. Установившимся режимам вращения ротора соответствуют значения to = cov, определяемые равенством
L(co) = /?(co)-V(to), (13.3)
т. е. точки пересечения соответствующих кривых па рис. 13.1, а, 3 (отметим, что кривая L(со) примерно отвечает характеристике асинхронпого электродвигателя). В зависимости от расположения кривой L(со) таких точек может быть от одной до трех. При этом, как показывает исследование (см. ниже), точкам типа соVi и ©vs отвечают устойчивые, а точкам типа ov2 — неустойчивые движения. В итоге оказывается, что ниспадающий участок резонансного пика классической резонансной кривой является нереализуемым.
Если бы ротор был установлен на неподвижном осно - вапии, то частота его установившегося вращения со0 — так называемая парциальная угловая скорость (см. п. 12.3.2) — определялась бы из уравнения
L(a) = R(a). (13.4)
Как видно из рис. 13.1, а, 3, co0>cor, (s = 1, 2, 3), т. е. в данном случае всегда имеет место торможение ротора.
Вообразим теперь, что мы плавно увеличиваем вращающий момент двигателя L, а тем самым и подводимую мощность N = La, стремясь увеличить частоту вращения ротора о); в условиях рпс. 13.1. а, 3 это соответствует переходу от кривой Li к крпвьтм L и />2. Если ротор
устапошіеп па неподвижном оспопаппп, то со столь же плавно возрастает (кривая 1 на рпс. 13.1, о, 4). Если же |іоюр связан с колебательной системой, то наблюдается следующая примечательная закономерность, часто пазы - наемая эффектом Зоммерфелъда: на начальном участ - )о ОА, когда вибрационный момент относительно мал, частота со увеличивается примерно так же, как при вращении ротора па неподвижном основании. Затем, когда чистота со приближается к частоте свободных колебании р, увеличение со происходит очень медленно, несмотря на существенное увеличение подводимой мощности N (уча - пок АВ), сопровождающееся ростом амплитуды колебаний А. Наконец, при определенном значении N = N* происходит скачкообразное увеличение частоты со до некоторого послерезонанспого зпачения со*; амплитуда колебаний также резко падает. При дальнейшем плавном увеличении N частота со снова изменяется плавно (участок CD).
В литературе описаны интересные проявления рассмотренного эффекта. Так, известен случай, когда судовой двигатель упорно но выходил на номинальное число оборотов га0, несмотря на вполне нормальное достаточно низков трение в валопроводе. Причина обнаружилась случайно. Выяснилось, что подводимую мощность «отсасывает» участок стального каната, лежащего па палубе: частота его свободных колебаний оказалась несколько меньшей п0, и при приближении к ней он начинал интенсивно вибрировать. Известны также случаи, когда машинисту локомотива не удавалось увеличить скорость движения поезда до желаемого значения, несмотря на соответствующее передвижение ручки контролера. Скорость скачкообразно увеличивалась лишь при заметном превышении подводимой мощностью обычно требуемого уровпя. Причина состояла в том, что вблизи определенного значения скорости частота колебаний вагонов, возбуждаемых прохождением колесами стыков рельсов, оказывалась близкой, например, к частоте колебаний жидкости в неполпостью заполненных цистернах. Этот случай интересен, в частности, тем, что колебания, «отсасывающие» энергию, обусловлены не неуравновешенностью ротора, а другой причиной, хотя механизм явления остается прежним.
Впрочем, значение обсуждаемого эффекта определяется не только такими экзотическими случаями, но и ею прямым отношением к распространенному в вибра -
цігонпой технике способу возбуждения колебаний посредством неуравновешенных роторов (механических инерционных вибровозбудителей). Значительная неуравновешенность ротора в этпх случаях создается преднамеренно, и поэтому эффект стабилизации частоты и срыва резонансного реяшма при колебаниях нагрузки здесь весьма существен. В качестве другого приложения укажем так называемый регулятор Буасса — Сарда
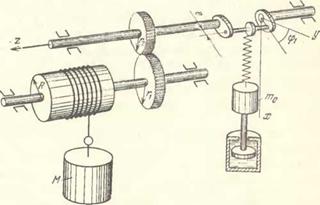
|
Рис. 13.2. Вибрационный стабилизатор скорости опускания груза (регулятор Буасса—Сарда). Стабилизация происходит при скоростях опускания груза, которым соответствуют частоты колебаний инерционного елемента регулятора, близкие к частоте свободных колебаний р — Ус/т (см. также рис. 13.1, а) |
(рис. 13.2). Здесь эффект стабилизации частоты колебаний (а тем самым и скорости опускания груза) вблизи резонансного значения р —Т/с/М играет положительную роль,