Мнкровиброреология: поведение суспензий при вибрации, эффективная вязкость н эффективная плотность суспензий
5.1.1. Бесструктурные суспензии — твердые частицы п вязкой жидкости. Существенные для вибрационной техники н технологии эффекты, о которых поіідет речь в настоящем пункте, во-первых, не обязательно относятся к числу нелинейных, во-вторых, относятся к микровиброреологии, а в-третьих, касаются «быстрых» движений,
В вибрационной технологии часто приходится иметь дело с заполненными суспензией объемами, которым сообщаются гармонические колебания заданной частоты ш и амплитуды А (рис. 6.4, а). При этом возникают по крайне* мере три следующих важных вопроса: 1) каковы абсолютная и относительная амплитуда колебаний частиц твердоіі фазы; 2) какую силу необходимо приложить к единичному объему суспензии для обеспечения указанных колебании; 3) каковы при этом затраты энергии?
Проще всего ответить па эти вопросы, если частицы являются шарами одинакового диаметра d = 2г, взвешенными в вязкой несжимаемой жидкости, причем их объемная концентрация с в рассматриваемом объеме пе слишком велика, так что можно не учитывать взаимного
|
|
|
|
|
|
|
|
|
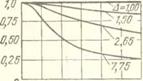
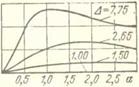
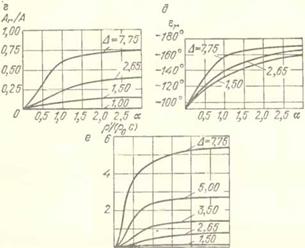
Рис. 6.4. Если подвергнуть гармоническим колебаниям сосуд с суспензией, то твердые частицы будут совершать колебания относительно жидкости тем большей амплитуды, чем больше плотность частиц отличается от плотности жидкости. Эффективная плотность суспензии при колебаниях будет всегда меньше плотности суспензии: а) схема системы; б) отношение амплитуды абсолютных колебаний частиц к амплитуде колебаний сосуда; в) сдвиг фаз абсолютных колебаний; г, Э) то же для относительных колебаний; е) относительное эффективное уменьшение плотностн суспензии |
|
20 АО к |
влияния частиц. Как показывает исследование [82], для этого с не должно превышать примерно 5%, что соответствует расстоянию между частицами, не меньшему двух-трех диаметров[16]). Приведем соответствующие результаты [81—85].
Закон колебаний объема считается заданпым в форме £ = 4sin(i)£, относительные колебапия частиц получаются в виде хт — Л г sin {at + єг), а абсолютные — в виде ха = = 40sin(coi + Ео), причем
Л2 + д(і + Аа-і] + 4- +
+ - jq a-4 fl + 2а + 2а2 +
|
1/2 |
|
к |
Здесь Д = р/р0 — отношение плотности материала частиц к плотности жидкости, а ос = rVco/(2v), где V — коэффициент кинематической вязкости жидкости, Графики зависимостей (6.8) представлены па рис. 6.4, б—д. Как следует из формул и графиков, амплитуда относительных колебаний частиц А, тем больше, чем больше их плотность отличается от плотности жидкости; колебания частиц более плотных, чем жидкость, отстают по фазе от колебаний объема — сдвиг фаз єг лежит в пределах от —я/2 до —л. С ростом параметра а эти амплитуды возрастают, а сдвиг фаз асимптотически стремится к —л. В абсолютном движении частицы, болое плотные, чем жидкость (А > 1), будут, отставая но фазе, колебаться с амплитудами Аа, меньшими амплитуды колебании объема, а менее плотные (А < 1), опережая по фазе,— с абсолютными амплитудами, превосходящими амплптуды колебаний объема.
Сила р, необходимая для обеспечения гармонических колебаний единичного объема суспензии, может быть представлена в форме
р=р*і+к*і (6.9):
где
р* = р. - р' (6.10)
— величипа, которую можно назвать эффективной плотностью суспензии при колебаниях [83]; вследствие подвижности частиц она оказывается меньшей плотности суспензии
р3 = ри(1 - с)+ Ф = р„[1 + с(Д - 1)] (6.11)'
па положительную величину р', определяемую по формуле
Графики зависимости относительного эффективного (кажущегося!) умеиьшеыия плотности суспензии при колебаниях р'/р0с от Д и а представлены на рис. 6.3, е. Для величины к, которую можно назвать эффективным коэффициентом демпфирования, получается выражение
к* р0ссо (1 + а) а~2 (А2Г/А2), (6.13)
Мощность, которую пеобходимо затратить па поддержание колебаний единичного объема суспензии,
N = (рІУ = у к*А2 = і - р0с« (1 + а) ЫгА. (6.14)
Формулы (6.8) —(6.14) справедливы прп условии, что либо число Рейнольдса Re = ^rcod/v мало по сравнению с единицей, либо число Струхаля Sh = d/Ar достаточно велико по сравнепшо с единицей. В работе [84] можно найти результаты, относящиеся к более общему случаю. Заметим также, что в пределах справедливости указанных формул нетрудно, пользуясь принципом суперпозиции, получить соответствующие результаты для случаев произвольного периодического закона колебаний суспензии, а также для суспензии, состоящей из частиц различных размеров и плотностей. Можпо рассмотреть также задачу о колебаниях в суспензии крупных, но срав-
нению с частицами твердой фазы и с расстоянием между ними, твердых тел. В этом случае естественно возникает понятие о вибровязкости суспензии [85].
|
|
|
F(&y |
2)
Hsmwt
Rr/(2A*) 1>А *=mo (A-VA/mj
|
1 0,8 0,6 0,4 0,2 |
2) A =A
Ц1 0,2 0,3 0,4 [0,00,6 0,7 0,8 0,9 1,0 0,472
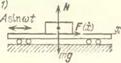
Рио. 6.5. Твердая частица, лежащая на горизонтальной шероховатой плоскости или помещенная в среду с сопротивлением типа сухого трения, при достаточно интенсивных колебаниях плоскости или среды совершает относительные колебания с полуразмахом Rr ; этот эффект используется в просеивающих машинах, в машинах для интенсификации процессов и для обработки деталей: а) схема системы (J—частица на вибрирующей поверхности, г —частица в колеблющейся среде); б) зависимость относительного полуразмаха ЙГ/(2А») от параметра г U—область относительного покоя, 11— область попеременного скольжения с остановками конечной продолжительности, 111 — то же с мгновенными
остановками)
Отметим, наконец, что в случае, когда вязкостью жидкости можно пренебречь, т. е. когда а< 1, формулы (6.8)
ц (6.12) резко упрощаются, принимая вид
Аг | А — 11 2 [ Р — Рп |
А Л+ 1/2 2р0+р ’
3 Зр, п й г
~ ~ 2Д_+ 1 ~ 2р0 + р’ Єг = — Єа~ ■’ ^
P' 2 (Р ~ Р0)2
Р0С Р0 (2Р + Ро) ’
Описанные закономерности поведения суспензий при вибрации используются для интенсификации технологических процессов н ускорения химических реакций (см.
раздел 10), а также при создании приборов для измере - ния запыленности среды (раздел 17).
6/1.2. Структурированные суспензии — частицы в среде с сопротивлением типа сухого трения. Если сила сопротивления среды относительному движению частицы носит характер сухого трения, то для величины полуразмаха относительных колебапий Нт вместо графиков рис. 6.4 получаем кривую, представлепную на рис. 6.5. Величина Rr/(2A*) в этом случае зависит от двух параметров
Z = -------- ----- Т-, zx = (6.16)
т0 (Д - 1) 1 1 т0 (Д — 1) Лша 1
причем А* = т0(А — .)А/т{, где ті есть масса частицы с учетом присоединенной массы среды, т0 — масса среды в объеме, равпом объему частицы, Д = р/р0 — как и выше, отношение плотности частицы к плотности среды, F{ a F — соответственно сила сухого трения покоя и скольжения; при построении графика припято F = 0,7Fi. При z > 0,7 в условиях рис. 6.5, б частица движется вместе со средой, при 0,472 < z < 0,7 — скользит попеременно вперед и назад, останавливаясь при перемене направления скольжения па конечные промежутки времени, а при г <0,472 — мгновенно изменяя направление скольжения.
График рис. 6.5, б получается в результате решения дифференциального уравнения относительного движения частицы в среде
mj£ = т0(А — 1)Лмгsin юг ^ F (f#0),
(0.17)
— Fi < то(А — 1)<4ю! sin at < Ft (і = 0),
которое получается ттз уравпепия (7.13) следующего раздела, если положить g = 0. В свою очередь уравпение (6.17) с точностью до обозначений совпадает с уравпеписм движепия частицы по горизонтальной шероховатой плоскости, совершающей продольные гармоппческие колебапия, подробно рассмотренным Л. Г, Лой - цянским [141], а затем в кпиге [30].