ОСНОВНЫЕ ТЕХНИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПРЕОБРАЗОВАТЕЛЕЙ
Погрешность преобразования
Любой аналого-цифровой преобразователь характеризуется функцией преобразования увых={(хВх), являющейся характеристикой преобразования вход—выход. Любые отклонения реальной характеристики (т. е. характеристики, присущей отдельному образцу преобразователя и зависящей от режима работы, влияния внешних факторов, условий нагрузки и т. д.) от идеализированной (паспортной) представляют собой абсолютные погрешности преобразования.
Общая погрешность преобразования складывается из динамической погрешности, возникающей из-за изменения входного сигнала за время формирования разрядов числа tKB и инерционности элементов измерительной цепи, и статической погрешности ^погрешности отдельного измерения). Последняя характеризуется рядом составляющих, число которых зависит от типа преобразователя. Из них отметим {Л. 8, 9] погрешность дискретности Ад, являющуюся методической, так как определяется методом преобразования; дрейф нуля преобразователя Ан; погрешность As от изменения крутизны 5 преобразователя во времени и под влиянием внешних факторов; нелинейность истинной характеристики преобразования Дл; погрешность от воздействия помех Ап.
Погрешности Ан, Ав, Ал, Ап являются составляющими инструментальной погрешности Дин, так как они связаны с несовершенством измерительного. прибора.
Следует отметить, что шумы и помехи выявляются на выходе преобразователя и приводятся к его входу точно так же, как и
Дрейф нуля. Поэтому обычно погрешности от этих составляющих учитываются как общая погрешность дрейфа нуля До.
Для однозначного определения суммарной погрешности АИн должны быть известны допустимые значения составляющих погрешностей, законы их распределения в полях допусков и заданная доверительная вероятность суммарной погрешности.
Зная статистические характеристики распределения составляющих, такие как математическое ожидание Л1 (Ао), M(AS), М(АЛ) и среднеквадратичное отклонение от математического ожидания oi(iAo),
|
Рис. 5. |
cr(As), сг(Ал), и предполагая, что Ао, Д8, Ал независимы, Лі(АИн) и сгі(Айн) определим из 'выражений
М (Айн) = М (А0) + М (А.) + М (Ал);
О (Дин) = V [» (До)]2 + ]а (Д«)]2 + [• (Д»)]2-
Предельное значение суммарной погрешности определяется выражением
Аин. маКс ==
|М(Аиа)±ев(АИн)|,
где 8 — коэффициент, определяемый заданной доверительной вероятностью того, что погрешность не выйдет за границы Аин. макс, а также законом распределения суммарной погрешности.
Значения 8 определяют по таблицам интеграла кривой распределения вероятностей Гаусса, задаваясь доверительной вероятностью Р. Общий выбор доверительной вероятности Р производится исходя из соображений, например, технико-экономических, допустимого процента брака, степени ответственности измерений, разумного сочетания точности и экономичности прибора и т. д.
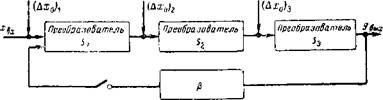
Рассмотрим измерительную цепь, состоящую из нескольких преобразователей с известными характеристиками (рис. б). Оценим 'влияние обратной связи на характеристики преобразования, в качестве которых выберем основные — относительную погрешность у8 от изменения крутизны S функции преобразования (ys—ASIS, где AS — изменение крутизны преобразователя) и погрешность от дрейфа нуля, действия шумов и помех A*0-
Если измерительная цепь состоит из трех элементарных преобразователей, имеющих крутизну преобразования соответственно 5ь 5з, то общая крутизна преобразования 5=5і5г5з и
Пусть (Л*о)і, (А^о)г, (Д*о)з— соответственно сигналы, эквивалентные 'Приведенным к івходаїм значениям дрейфа нуля, шума и помехам каждого звена. Трансформируя эти сигналы на вход измерительной цепи, получим:
л /л I (^*0)2 t
AXq (А^О/1 • £ о 2 *
т. е. погрешность измерительной цепи от изменения крутизны преобразования является суммарной погрешностью элементарных пре
образователей и не ізависит от порядка расположения преобразователей. Наиболее жесткие требования должны. предъявляться к первому элементарному преобразователю.
Если цепь обратной связи замкнута, крутизна характеристики преобразования преобразователя с обратной связью определяется выражением
где (3 — коэффициент передачи цепи обратной связи, и
_ASq. c_AS 1 Ар S$
*^so. c *^О. С *“> ^ Р 1 ~Ь
При условии, что 1,
1 Ар 4.C-Ys р •
Отсюда следует, что снизить погрешность измерительной цепи от изменения крутизны преобразования - путем введения отрицательной обратной связи можно только в том случае, если имеется возможность получить хорошую стабильность звена обратной связи. Следует учитывать, что повышение точности сопровождается потерей чувствительности.
Определим погрешность (Дхо)о. с в схеме с обратной СВЯ'ЗЬЮ. Погрешность от дрейфа нуля, действия помех и шума на выходе измерительной цепи определяется выражением
S 5 *S 5 S S
(Д*/о)о. с = (ДЯо)і J Ь (^#0)2 і _|_ (Дх0)в 1 _|_ 5^*
Учитывая, что і(Д*/о) о. с/£о. с= (Л*о) о. с— приведенная ко входу измерительной цепи погрешность от дрейфа нуля, действия помех и шума, можно написать:
°1
Как видно, обратная связь не изменяет величину приведенного ко входу измерительной цепи дрейфа нуля и уровня помех и шума прямой цепи преобразователя. Относительная погрешность преобразователя, обусловленная помехами, шумом и дрейфом нуля, трансформированная на вход, выразится:
л _
Х ~~ *макс ’
где Хманс — максимальное значение сигнала на входе измерительной цепи.
•В цепи с обратной связью максимальный входной сигнал при неизменном выходном должен быть увеличен В (1+SP) раз вследствие уменьшения крутизны преобразования. Поэтому
«ч ^хо _
■^О. с #маКс О + *S|0
Следовательно, отрицательная обратная связь повышает помехоустойчивость преобразователя, но связана с лотерей чувствительности, т. е. с повышением уровня входного сигнала преобразователя. Можно (повысить помехоустойчивость и без обратной связи, уменьшая крутизну прямого тракта измерительной цепи, однако в этом случае погрешность от нестабильности общей крутизны тракта остается нескорректированной.