ЧАСТОТНОЕ УПРАВЛЕНИЕ АСИНХРОННЫМИ ДВИГАТЕЛЯМИ

Закон постоянного полного потока

Масштаб моментов не зависит от частоты:

Первичное напряжение на выводах статора (или «внут­ренняя» ЭДС инвертора, если его активное сопротивление добавить к сопротивлению статора) имеет геометрическим местом, при каждом значении частоты, свою собственную окружность (рис. 2.7):

P»=0'* + V». Очевидно, эта окружность hrt повторяет окружность тока, построенную в соответствующем масштабе напряже­ний у конца вектора внутреннего напряжения О'. С из­менением частоты она будет перемещаться параллельно самой себе и окружности токов. Чтобы не перемещать эти окружности, можно построить одну окружность для всех частот у основания вектора напряжений U', развернув ее на 180°. Эта окружность определит векторы падения на­пряжения 1'іГі с обратным знаком, а вектор напряжения на выводах представится отрезком между концами векто­ров: О', пропорционального частоте, и /іп, не зависящего от частоты.

Распределение на окружностях Д и /іГі точек абсолют­ного скольжения (3 находится совершенно так же, как и на окружности тока.

Геометрическими местами постоянного абсолютного скольжения для напряжения на выводах О будут прямые.

О— £^ном а+/"і/і(Р).

Это следует непосредственно из уравнения (2.4), так как ток есть функция только одного параметра абсолют­ного скольжения р.

Уравнения основных прямых напряжения при p=const: напряжение идеального холостого хода

Uo—-ІОГ1+ U ііомЯ,

напряжение идеального короткого замыкания

UjK:=IjKrі + О HOlrfCl,

вектор центра окружности напряжения

pU = rtpc + p’mMa.

Эти уравнения определяют и распределение па прямых точек параметра частоты а. Пользуясь двумя прямыми (2.7) и (2.8), легко построить окружность напряжения для любого значения частоты.

Уравнение момента в зависимости от абсолютного скольжения р можно получить из общего уравнения (1.20), положив в нем rt—0. Тогда <7=0 и

2

М = Мтах Р/Р^р + ркр/р -

Выражение для максимального момента получим с учетом обозначений (1.10), подставив U'цом вместо С/ВоМ,

xi О + х) + хГ2 (1 + ті) - ^ ^

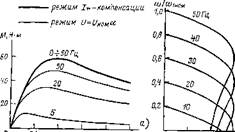
Важно, что в рассматриваемом режиме максимальный ломент не зависит от частоты благодаря компенсации па­дения напряжения ІіГі.

Критическое значение параметра абсолютного скольже - шя Ркр получим из (1.19), подставив ri=0:

г'гУ +1.)

8 --

Ркр *i(l +Т2) +х'г

Критическое значение скольжения sKp изменяется об­ратно пропорционально частоте статора:

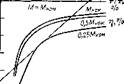
На рис. 2.8 приведена одна кривая момента для всех іастот в зависимости от параметра абсолютного сколь­жения р. Там же для сравнения показаны кривые момента з номинальном режиме U—Unoyia для частот 50, 20 и 5 Гц.

Выразив в уравнении момента (2.9) параметр абсолют­но скольжения р через относительные величины частоты і и угловой скорости ротора v=a—р, получим выражение механической характеристики двигателя

м=м,

На рис. 2.8,6 показано семейство кривых относительной Аловой скорости v в зависимости от момента М при по - 164

стоянных значениях частоты 10, 20, 30, 40, 50 Гц. Крутизн механических характеристик изменяется, остается ней менной для всех частот при любом постоянном значена момента. Параметр абсолютного скольжения р при любе значении момента не зависит от частоты:

'max

Рабочий поток двигателя может быть определен исхо; из формулы (1.17) подстановкой в нее ип0м=и'тк, гі—

Y = a:

Поток не зависит от частоты, а от нагрузки он зави« так же, как при поминальной частоте. Относительное зн чение потока

(*2 2 + г2 2/Е2) (с* + e2r’2 VSH0M)

(*2 2 + r'afs2ном) (С2 + е% 2/?2)

Электромагнитные потери можно выразить через ме мент двигателя, используя (1.47), формулой (1.52) с по, становкой в нее р из (2.12):

На рис. 2.9 показаны рабочие характеристики двигате ля в режиме постоянного полного потока в относительны, единицах — напряжение у, поток ср и КПД в зависимост. от частоты а. Поток показан двумя прямыми <p=const пр номинальном моменте и при холостом ходе, когда он пе сколько возрастает. КПД показан тремя кривыми при немнналыюм моменте, его по ловиие и четверти. С умень - 100 шением нагрузки КПД gQ уменьшается, так как потери

или несколько большее значение при холостом ходе, pai иое с точностью до потерь в стали

^НОМ_____ 5___

^номо '

Ф

VcP + >

Соответствующее этому потоку «номинальное» значені ЭДС

Т Jt Г f? UПГ)Т UцпТ

U ипМ ^Н1

1 + '

Уравнение геометрически мест и характеристик двигате. в режиме d>=const можно пол чить, как и в режиме /іГі-компе. сации, из общих уравнений гл. ПОЛОЖИВ В НИХ Гі = О, Т]=0, %■

—%2, в результате чего напр жепие V' становится равнь входному.

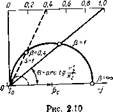
Ток холостого хода не зав сит от частоты и описывается п стоянным вектором (рис. 2.10).

j _Ог0а Uо 0 г0а — г0 + jx0 •

Вектор приведенного тока ротора

I _ й"о<* [0"0

4" Іх'г

вектор первичного тока

Іі = Іо+^2

будет описывать окружность, радиус которой а координата центра

рс=Л) + $с.

Ток идеального короткого замыкания (|3=оо) Ак = Д + 2/?с = — jU"

Положение точки короткого замыкания на окружност] тока при любой частоте /і=/іном<х просто определяется пі 68

ШКалё параметра скольжения, построенной при номиналь­ной частоте но угловому аргументу

tg ст=г/2/ ХГ2.

Луч, проведенный из конца вектора /0 в точку шкалы скольжения, в которой s=a, даст на пересечении с окруж­ностью точку короткого замыкания при частоте, соответст­вующей а.

Компенсация падения напряжения в полных сопротив­лениях статора требует существенного повышения напря­жения с возрастанием нагрузки.

На рис. 2.10 для сравнения пунктиром показана окруж­ность токов в режиме постоянного потока (г 1=0). Она очень мало отличается от окружности в номинальном ре­жиме Uіном, /1 Іном*

С изменением параметров а и (3 первичное напряжение Uі описывает геометрические места, уравнение которых по­лучим, подставив в (2.13) первичный ток

''о + r't (1 + тг)

^ 0 — (*о — />о)я'2 + (''o + /*o)'V? ‘ (2.14)

Отсюда напряжение

А + В - у-(-С - J--j-Da f/T = f/”0 ^1 , (2.15)

Фиксируя параметр скольжения (3, получим уравнение геометрических мест постоянного абсолютного скольже­ния — прямых

Р-14

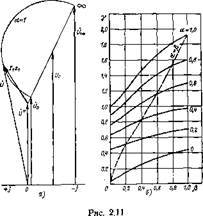
Ha рис. 2.11,а показан вид геометрических мест вектора первичного напряжения в режиме постоянного потока при нбминальной частоте (а=1). Для каждого значения ча­стоты нужно строить свою окружность напряжения.

Разметка шкал параметра « для каждой прямой р= =const дается по двум точкам прямой: а=0 и а=1. Хор­да, соединяющая две точки шкал р=0 и р=оо с одинако­вой отметкой а=а*, дает диаметр окружности, представ­ляющей собой геометрическое место конца вектора напря - 70 жєния по параметру абсолютного скольжения при данной частоте мі=мінома. Точка пересечения диаметра с прямой центров является центром окружности. Шкала параметра р для каждой окружности а = а* строится так же, как шка­ла скольжения на окружностях тока: проводится прямая параллельно диаметру, ее отрезок между перпендикуля­ром к диаметру из его конца р=0 и точкой пересечения с линией полезной мощности, т. е. хордой, соединяющей

точки р=0 и р=1 (или ее продолжением), и дает шкалу, масштаб которой определен этими точками.

На рис. 2.11,6 приведены кривые, характеризующие из­менение напряжения в режиме постоянного потока у в за­висимости от р при различных постоянных значениях ча­стоты статора а. Пунктиром показана граница области двигательного режима, расположенной слева, т. е. кривая пусковых моментов s=l, а=р.

Эти кривые, так же как и рис. 2.10, показывают, что в режиме постоянного потока, в верхнем поддиапазоне ча­стот напряжение значительно превышает номинальное, особенно при больших скольжениях в пусковых режимах. Это ограничивает использование режима <I>=const в ука­занных условиях.

Вместе с тем существенно возрастает момент двигате­ля, что и является преимуществом этого режима. Макси­мальный момент в режиме постоянного рабочего потока больше, чем в режиме постоянного потока, т. е. /^-ком­пенсации (и приблизительно в режиме LJ=UWома) в отно­шении

М"max х 0 4" т) Ч~ х'г (I Н~ ті)

М'max х'г

В примере, показанном на рис. 2,10 и 2.11, максималь­ный момент увеличивается в 2,4 раза.

Практическое применение режима постоянного потока ограничивается допустимым повышением напряжения.