ЧАСТОТНОЕ УПРАВЛЕНИЕ АСИНХРОННЫМИ ДВИГАТЕЛЯМИ
Трансеекторное управление (FOC)
Как известно, полная управляемость электропривода обеспечивается, если обеспечивается управление электромагнитным моментом двигателя. Во всех электромеханических преобразователях вращающий момент образуется в результате взаимодействия магнитных полей статора и ротора или, что то же самое, магнитного поля одного элемента и тока другого. Для получения однозначных функций управления обе величины должны быть независимы друг от друга, и тогда одну из них можно поддерживать постоянной, а с помощью другой осуществлять регулирование. В ДПТ и синхронных двигателях существуют отдельные электрические цепи для управления магнитным потоком и моментом. В короткозамкнутых АД есть только один канал, в котором объединены обе составляющие тока и в задачу системы управления входит функция их разделения. Математически эта задача элементарно решается при использовании уравнений обобщённой электрической машины в векторной форме. В результате выбора пары векторов величин образующих электромагнитный момент и системы координат, в которой они представлены, можно получить уравнение момента в виде функции независимых проекций этих величин на координатные оси. И тогда управление моментом сведется к управлению проекциями векторов. Отсюда и происходит название способа.
В 1971 году Ф. Блашке (F. Blaschke) сформулировал принцип управления, запатентованный фирмой Siemens и названный трансвекторным управлением (TRANSVEKTOR® - Regelung). Математической основой его являются уравнения электромагнитных процессов в АД в векторной форме, представленные в системе координат ориентированной по направлению магнитного поля. В англоязычной литературе этот принцип называется field-oriented control (FOC), т. е. «управление с ориентацией по полю». Он успешно используется до настоящего времени и полностью ассоциируется с понятием векторного управления, хотя в последнее время с развитием устройств обработки информации появился другой способ, в котором также используется векторное представление величин, но алгоритм управления отличается от трансвекторного. Этот способ называется прямым управлением моментом (DTC direct torque control) и также будет рассмотрен далее. В дальнейшем для разделения понятий мы будем использовать для первого способа название трансвекторное управление.
Выбор уравнения электромагнитного момента АД и системы координат
Для построения систем векторного управления АД могут быть использованы любые пары векторов, с помощью которых можно представить электромагнитный момент обобщённой электрической машины. Однако от выбора векторов в значительной мере зависит степень сложности системы. Желательно, чтобы величины, представленные векторами в уравнении момента были наблюдаемы, т. е. чтобы их можно было непосредственно измерить и воздействовать на них при управлении моментом. У короткозамкнутого АД есть только две такие величины - это напряжение и ток статора, и только одна из них, а именно ток статора, может входить в уравнение момента. Тогда другой величиной может быть только ток ротора или какое-либо потокосцепление. Ток ротора принципиально ненаблюдаем, а устройства его идентификации по наблюдаемым параметрам сложны и ненадежны. Поэтому для выбора остаются три потокосцепления: статора, ротора и основное, т. е. магнитный поток в зазоре АД. Потокосцепление статора и рабочий поток АД можно непосредственно измерить и использовать этот сигнал в системе управления, что часто и делается при создании приводов высокого качества. В массовых же изделиях разработчики стараются использовать сигналы, доступные без установки датчиков, т. е. все те же ток и напряжение статора, по мгновенным значениям которых можно вычислить, например, пото-
ixrx + vj/j = І (ц - ixrx) dt. Однако при выборе
потокосцепления статора или основного потокосцепления передаточные функции системы управления получаются довольно сложными и мало подходящими для практического использования.
Простейший вид имеют уравнения электромагнитных процессов в АД в случае представления их через вектор потокосцепления ротора j/2. То обстоятельство, что vj/2 невозможно измерить не является препятствием для выбора, т. к. магнитный поток ротора легко вычисляется по потоку статора или по рабочему потоку. Поэтому в дальнейшем мы ограничимся рассмотрением наиболее распространенных систем, использующих для регулирования электромагнитного момента ток статора и потокосцепление ротора и соответствующее уравнение момента.
Поскольку форма уравнений потокосцеплений инвариантна к выбору системы координат, то в произвольной системе тп уравнение момента будет иметь вид
|
|
|
Векторы |/2 и ix вращаются в пространстве с угловой частотой со, = 2тіґх / zp. |
|
(2.12) |
Поэтому если для описания процессов выбрать неподвижную систему координат или систему координат, вращающуюся синхронно с ротором АД, то проекции векторов будут синусоидальными функциями времени и регулирование таких величин будет сложной технической задачей. В случае же выбора системы коор-
динат вращающейся в пространстве с синхронной частотой со1, проекции векторов будут постоянными величинами, и управление будет не сложнее, чем управление токами якоря и возбуждения ДПТ.
|
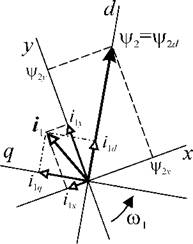
Рис. 2.15 Векторы определяющие электромагнитный момент в произвольной синхронной (ху) и ориентированной по полю (dq) системах координат. |
Задачу управления можно еще более упростить, если совместить какую-либо ось системы координат с одним из двух векторов. Тогда проекция опорного вектора на эту ось будет равна его модулю, а другая проекция будет равна нулю. При этом в уравнении электромагнитного момента (2.12) исчезнет соответствующее слагаемое в правой части.
Следовательно, если для управления электромагнитным моментом АД выбрать векторы потокосцепления ротора и тока статора и синхронную систему координат dq,
совместив ось d с вектором |/2, то уравнение (2.12) примет вид
который в принципе ничем не отличается от соответствующего выражения для ДПТ и основной задачей системы управления будет идентификация проекций цJ2d и ilq. Если при этом управление построить так, чтобы потокосцепление ротора сохранялось во всех режимах постоянным, то регулирование момента АД будет осуществляться изменением поперечной составляющей тока статора ilq,
выполняющей в такой системе функцию тока якоря.
Следует заметить, что в ориентированной по магнитному полю системе координат не только исключается влияние продольной составляющей тока статора ild на векторное произведение, т. е. на электромагнитный момент АД, но с помощью этой проекции становится возможным управлять магнитным потоком. Это объясняется с тем, что ток статора в короткозамкнутом АД определяет все процессы в машине и если одна из его компонент не влияет на момент, то она тем или иным способом должна быть связана с магнитным потоком. В то же время, система координат dq ортогональна, поэтому изменение одной из проекций тока
никоим образом не влияет на другую, и управление моментом и потоком может производиться независимо.
Таким образом, принцип трансвекторного управления заключается в раздельном управлении магнитным потоком и моментом АД с помощью независимых составляющих тока статора, соответствующих проекциям вектора тока на оси системы координат, ориентированной по направлению вектора магнитного потока.
Это определение полностью подходит и для ДПТ, если токи возбуждения и якоря объединить в вектор, представленный в системе координат, ориентирован
ной по оси главных полюсов. Отличие АД от ДТТТ заключается только в том, что в АД система координат вращается вместе с потоком, а в ДТТТ она неподвижна. Реальные же токи статора АД протекают в неподвижных обмотках и соответствуют проекциям вектора тока на неподвижную систему фазных осей координат. Поэтому при трансвекторном управлении АД необходимы координатные преобразования.
В неподвижной системе координат продольная и поперечная составляющие определяют амплитуду и фазу тока статора АД по отношению к магнитному потоку совершенно аналогично тому, как активная и реактивная составляющие определяют эти параметры по отношению к напряжению. Если задать значение продольной составляющей ild, соответствующим требуемому магнитному потоку, а поперечной ij - требуемому моменту на валу, то тем самым будет определен вектор тока статора в синхронной системе координат. После этого, в соответствии с выражениями (1.7), можно преобразовать синхронную систему координат dq в неподвижную аР и разложить вектор тока на фазные проекции, в результате чего образуются синусоидальные сигналы, соответствующие фазным токам которые нужно сформировать в обмотках статора, чтобы получить заданный электромагнитный момент.
Преобразование системы координат невозможно без информации о пространственном положении опорного вектора V|/2 в каждый момент времени. Эту
информацию можно получить непосредственным измерением магнитного потока статора или рабочего потока с помощью датчиков, а затем вычислить vj/2, или вычислить его по мгновенным значениям фазных напряжений и токов статора.
Трансвекторное управление реализуется техническими устройствами с различными функциями и алгоритмами, но суть его при этом остается неизменной и в дальнейшем мы рассмотрим несколько таких вариантов.
Модель АД, управляемого током статора
В синхронной системе координат dq, ориентированной по магнитному полю ротора (| \i21= \f2q = 0), уравнение ротора имеет вид
?МГг +^j— + joh'Vi4'1 =0
В это уравнение в качестве переменной входит неконтролируемый ток i2. Заменим его на ix, воспользовавшись выражением (1.13) для потокосцепления
|
ротора, из которого i2dq) ходное уравнение и, опуская индексы системы координат, получим Ч>2 |
|
L^. = d^ +Га+>2^ Ц, dt I |
ц/^ - Lmixdq^ /Ь2. Подставим это выражение в ис-
4=74i+T2p+jT2e>2)
Таким образом, с помощью продольной проекции тока статора ild можно независимо управлять потокосцеплением ротора и передаточная функция этого канала соответствует апериодическому звену с постоянной времени равной постоянной времени ротора. Продольная составляющая тот статора ild играет в АД роль тока возбуждения ДПТ или синхронной машины. Поперечная проекция ilq при постоянном потоке ротора позволяет безинерционно управлять частотой ротора со 2.
Подстановкой со2 = сог — со выражение (2.16) можно преобразовать и получить уравнение механической характеристики вида
со = со l-m/h, (2.17)
|
3zp4,2d 2 Го |
|
где h = |
|
СО |
|
— Р 1 АД! Р 1 АД2 J АД, |
|
'4,-v -^Хт^От |
|
Рис. 2.16. Электромеханическая характеристика АД при токовом управлении. |
|
|
|
со |
|
О |
|
ределяемая величиной потокосцепления 11|/21= yf2d - и активным сопротивлением г2 ротора. Выражение для жесткости идентично жесткости характеристики ДПТ, если в нем под сопротивлением якоря понимать г2. При i|J2d = const механическая характеристика линейна и полностью соответствует характеристике ДПТ с независимым возбуждением. Из выражений (2.14) можно определить электромеханическую характеристику АД со (7J. |
|
жесткость характеристики, оп- |
|
|
|
hm I hm |
|
) - ЦІТ2 |
Эта характеристика представляет собой параболу симметричную относительно частоты холостого хода сох (рис. 2.16), изменение которой будет приводить к параллельному смещению кривой. Увеличение мощности АД обычно соответствует увеличению постоянной времени ротора Т2, что приводит к росту относительного пускового тока /1п / I0m = -Jl + ^CDj)2 за счёт сближения ветвей параболы.
|
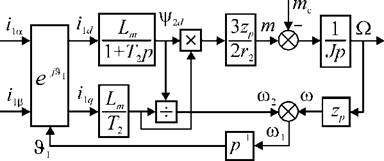
Рис. 2.17. Структурная схема АД при токовом управлении |
совместно с уравнением движения электропривода позволяют построить структурную схему АД представленную на рисунке 2.17. Входными величинами здесь являются проекции вектора тока статора ild и iXq, а также момент
сопротивления на валу АД тс. Однако в реальном АД
ток статора формируется в неподвижной системе координат еф в виде синусоидальных функций времени
определяемый как результат интегрирования угловой частоты статора = JcOjt/f = |(со2 + G))dt. Функцию преобразования координат выполняет внутренний блок вращения вектора тока или ротатор (е ^ на рис. 2.17).
Выражения (2.14) и приведенная на рисунке 2.17 структурная схема соответствуют проекциям вектора тока на ортогональные оси системы координат, что эквивалентно двухфазной машине. В действительности большинство АД трехфазные, поэтому в случае необходимости использования при анализе фазных токов уравнения и структурная схема должны быть дополнены на входе безинерционным блоком преобразования числа фаз в соответствии с выражениями (1.6 а). хронных машин в конце 20-х годов 20-го века. Модель АД, управляемого напряжением статора Управление АД можно осуществлять также с помощью проекций вектора напряжения статора на оси dq. Для этого нужно получить модель АД, в которой
входными величинами являются uld и ц Запишем уравнение статора АД в системе координат dq
= і^гх + >Wi№) • (2Л9>
Затем, пользуясь уравнениями потокосцеплений (1.13), представим потокосцепление статора через потокосцепление ротора и ток статора
Vi = І А О - Ккг) + W2k2 = hА + Угкг (2-20)
где: кх = Lm/ Z1; к2 = Ьт/~ коэффициенты электромагнитной связи статора и ротора; Ц = Ll( 1 - кхк2) - переходная индуктивность статора.
Опустим индексы системы координат и, подставив (2.20) в (2.19), преобразуем уравнение (2.19) по Лапласу. Тогда
щ = /[ [/; (1 + Тхр) + ргЦ] + Х|12к2 {р+рг)
где Т{= Ц/ц.
Разделяя проекции векторов в этом уравнении, мы получим с учетом того, что \J2q = 0, выражения для проекций напряжения и тока статора -
Uld = hd110 + Щ - hq® і А' + «гЛ (2 2^
Ц? = М I1 + TiP) + hd®iА' + «W2 А hd = фі + WіА' - /¥гЛ)
|
іц = Гі (і+щ (“lq~kd&iLv ~ )
|
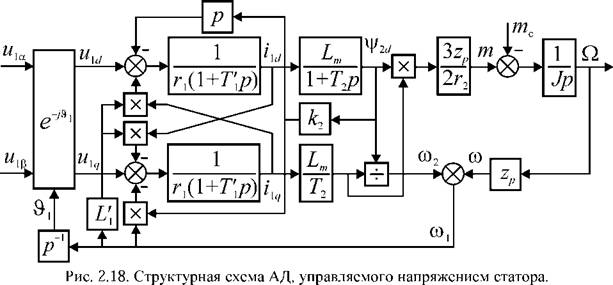
используя которые, можно дополнить структуру АД, управляемого током статора (рис. 2.17), и получить структурную схему АД, управляемого напряжением, показанную на рисунке 2.18. Входными величинами в ней являются проекции напряжений статора на оси dq и uXq. Здесь, также как при токовом управлении, проекции вектора напряжения в синхронной системе координат получены преобразованием uxdq) = иха^ ё~с помощью внутреннего ротатора (e~J&1 нарис. 2.18).
В случае необходимости анализа процессов с использованием реальных фазных напряжений в трехфазной машине структуру модели нужно дополнить безинерционным блоком преобразования числа фаз.
 (2.13)
(2.13)